|
механика_лабораторные работы. Контрольные вопросы для самопроверки. Пособие содержит методические указания по теории погрешностей. Работы расположены в последовательности изложения материала курса Общая физика, раздел Механика
Лабораторная работа №2
ПРОВЕРКА ОСНОВНОГО ЗАКОНА ДИНАМИКИ
ПОСТУПАТЕЛЬНОГО ДВИЖЕНИЯ
Цель работы: Убедиться в справедливости основного закона динамики поступательного движения.
Приборы и принадлежности: Модульный учебный комплекс МУК-М2: рабочий узел «наклонная плоскость», секундомер электронный СЭ1, брусок дерево-дюраль, два груза разной массы.
Краткое теоретическое введение
Основной закон динамики (или второй закон Ньютона) выражает соотношение между силой 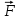 и изменением скорости (ускорением и изменением скорости (ускорением 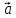 ) взаимодействующих тел: ) взаимодействующих тел:
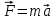 , (1) , (1)
где m – масса тела.
С помощью основного закона динамики можно определить силы, действующие на тело, либо характер движения (ускорение) по заданным силам. При составлении уравнения движения необходимо пользоваться следующим алгоритмом:
• вначале нужно найти все силы, действующие на данную материальную точку (включая силы реакции);
• затем следует найти равнодействующую этих сил;
• применить основной закон динамики и решить уравнение относительно неизвестной величины.
В данной лабораторной работе предлагается рассмотреть основной закон динамики на примере движения бруска массой m1по наклонной плоскости (рис.1).
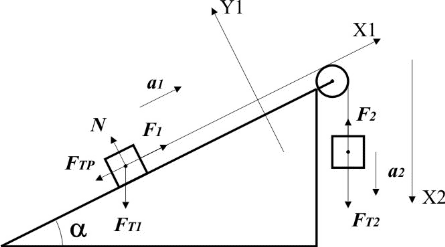
рис. 1
Для создания силы тяги 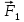 на невесомую, нерастяжимую нить, перекинутую через невесомый, вращающийся с малым трением блок подвешен груз массой m2. Груз под действием силы тяжести на невесомую, нерастяжимую нить, перекинутую через невесомый, вращающийся с малым трением блок подвешен груз массой m2. Груз под действием силы тяжести 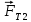 опускается, натягивает нить и заставляет брусок скользить равноускоренно по поверхности наклонной плоскости вверх. На брусок будут действовать: сила тяжести опускается, натягивает нить и заставляет брусок скользить равноускоренно по поверхности наклонной плоскости вверх. На брусок будут действовать: сила тяжести 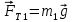 сила тяги сила тяги 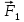 , сила трения , сила трения 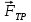 , сила реакции опоры , сила реакции опоры 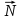 .На груз будут действовать сила натяжения нити .На груз будут действовать сила натяжения нити 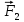 и сила тяжести и сила тяжести 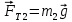 . .
Для описания движения бруска введем инерциальную систему отсчета, ось X1, которой сонаправим с ускорением 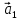 , а ось Y1 – перпендикулярно к наклонной плоскости. Движение груза будем рассматривать относительно системы отсчета, ось X2 которой направим по направлению ускорения , а ось Y1 – перпендикулярно к наклонной плоскости. Движение груза будем рассматривать относительно системы отсчета, ось X2 которой направим по направлению ускорения 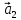 . .
Запишем уравнения движения бруска и груза в векторной форме:
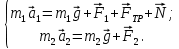 (2) (2)
Для решения полученной системы уравнений необходимо знать коэффициент трения μ, входящий в формулу для определения модуля силы трения 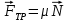 . Для нахождения этого коэффициента удобнее расположить наклонную плоскость под углом 0° к горизонту. В этом случае: . Для нахождения этого коэффициента удобнее расположить наклонную плоскость под углом 0° к горизонту. В этом случае:
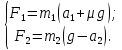 (3) (3)
Если считать, что блок невесомый и трение на оси блока отсутствует, то эти силы должны быть равны между собой по модулю. Поскольку нить нерастяжима, то ускорения a1=a2=a.Модуль ускорения aможно найти, зная длину пути L, пройденную бруском и время его движения:
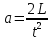 (4) (4)
Таким образом, решая уравнения (3), можно получить выражения для нахождения коэффициента трения скольжения:
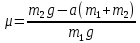 . (5) . (5)
Рассмотрим общий случай, при котором α≠0. Систему уравнений (2) в скалярном виде можно представить:
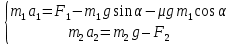 (6) (6)
Если выполняются условия F1=F2=F и a1=a2=a, то
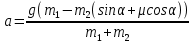 . (7) . (7)
Методика эксперимента
Исследовать движение бруска по наклонной плоскости можно с помощью узла «плоскость» и секундомера СЭ1, входящих в состав модульно учебного комплекса МУК-М2.
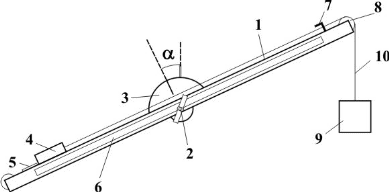
рис. 2
Установка представляет собой наклонную плоскость 1, которую с помощью винта 2 можно устанавливать под разными углами α к горизонту (рис.2). Угол α измеряется с помощью шкалы 3. На плоскость может быть помещен брусок 4. Для удержания бруска используется электромагнит 5. Пройденное бруском расстояние можно измерить с помощью линейки 6. На нить 10, перекинутую через блок 8 подвешивается груз 9.
В комплект узла «плоскость» входят два бруска и 2 груза различной массы. Каждый брусок состоит из двух частей, изготовленных из различных материалов: дерево-дюраль и дерево-сталь.
Порядок выполнения работы
Ослабив винт 2 (рис.2), установите плоскость под углом 0 к горизонту. Поместите брусок 4 (алюминий-дерево) на наклонную плоскость в положении деревом вниз.
Переключите тумблер управления электромагнитами механического блока в положение «плоскость».
Переведите секундомер СЭ1 в режим 1.
Нажмите кнопку «Пуск» секундомера. Измерьте время опускания груза.
Повторите опыт пятикратно.
Найдите ускорение бруска по формуле (4) и коэффициент трения по формуле (5). Сравните полученный в опыте результат с табличным значением коэффициента трения скольжения. Результаты всех измерений и расчетов занесите в таблицу №1.
Измените угол наклона. Опыт проведите пятикратно, взяв среднее время для расчета ускорения по формуле (4).
Минимум для пяти углов наклона повторите пункт 7. Результаты всех измерений и расчетов для дерева занесите в таблицу.
Постройте экспериментальную зависимость a(α).
Сравните полученный результат с теоретическим, найденным по формуле (7). Для расчета теоретического ускорения возьмите значение коэффициента трения скольжения μ из приложения.
Таблица
|
№
|
α
|
L, м
|
t, с
|
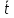 , с , с
|
a, м/с2 (эксп.)
|
а, м/с2 (теор)
|
μ
|
дерево
|
1
|
0
|
|
|
|
|
|
|
2
|
|
3
|
|
4
|
|
5
|
|
1
|
|
|
|
|
|
|
|
2
|
|
3
|
|
4
|
|
5
|
|
1
|
|
|
|
|
|
|
|
2
|
|
3
|
|
4
|
|
5
|
|
1
|
|
|
|
|
|
|
|
2
|
|
3
|
|
4
|
|
5
|
|
1
|
|
|
|
|
|
|
|
2
|
|
3
|
|
4
|
|
5
|
|
Постройте на одном графике теоретическую и экспериментальную зависимость a(α).
Повторите п. 1 - 9, повернув брусок в положение алюминием вниз.
Результаты всех измерений и расчетов для алюминия занесите в аналогичную таблицу.
Выведите формулы для абсолютной и относительной погрешности косвенного измерения экспериментального ускорения 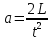 . .
Вычислите погрешности измерений.
Сделайте выводы.
Контрольные вопросы
Сформулируйте основной закон динамики поступательного движения?
Каков алгоритм при составлении уравнения 2-го закона Ньютона?
Какие силы рассматриваются в динамике?
Запишите уравнения движения бруска и груза в векторном и скалярном виде?
Как в данной работе вычисляется ускорение? Выведите формулу (4).
Как в данной работе находят коэффициент трения скольжения? Выведите формулу (5).
Решите систему уравнений (6).
*Как изменилось бы ускорение бруска и груза, если учесть трение в блоке?
Какими силами пренебрегли в данной работе?
Отличается ли экспериментальная зависимость а(α) от теоретической зависимости?
Какие погрешности присутствуют в работе?
|
|
|
 Скачать 0.7 Mb.
Скачать 0.7 Mb.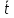 , с
, с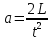 .
.
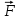 и изменением скорости (ускорением
и изменением скорости (ускорением 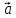 ) взаимодействующих тел:
) взаимодействующих тел: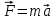 , (1)
, (1)
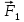 на невесомую, нерастяжимую нить, перекинутую через невесомый, вращающийся с малым трением блок подвешен груз массой m2. Груз под действием силы тяжести
на невесомую, нерастяжимую нить, перекинутую через невесомый, вращающийся с малым трением блок подвешен груз массой m2. Груз под действием силы тяжести 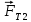 опускается, натягивает нить и заставляет брусок скользить равноускоренно по поверхности наклонной плоскости вверх. На брусок будут действовать: сила тяжести
опускается, натягивает нить и заставляет брусок скользить равноускоренно по поверхности наклонной плоскости вверх. На брусок будут действовать: сила тяжести 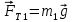 сила тяги
сила тяги 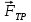 , сила реакции опоры
, сила реакции опоры 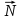 .На груз будут действовать сила натяжения нити
.На груз будут действовать сила натяжения нити 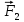 и сила тяжести
и сила тяжести 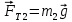 .
.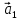 , а ось Y1 – перпендикулярно к наклонной плоскости. Движение груза будем
, а ось Y1 – перпендикулярно к наклонной плоскости. Движение груза будем 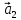 .
.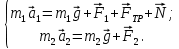 (2)
(2)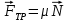 . Для нахождения этого коэффициента удобнее расположить наклонную плоскость под углом 0° к горизонту. В этом случае:
. Для нахождения этого коэффициента удобнее расположить наклонную плоскость под углом 0° к горизонту. В этом случае: 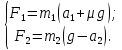 (3)
(3)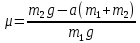 . (5)
. (5)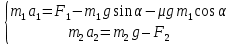 (6)
(6)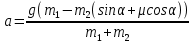 . (7)
. (7)