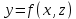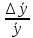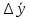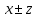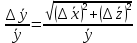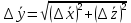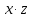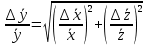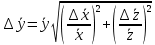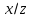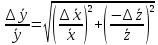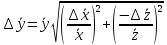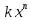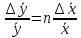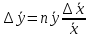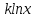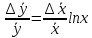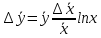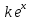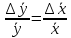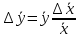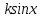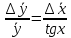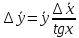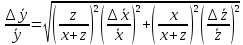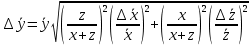механика_лабораторные работы. Контрольные вопросы для самопроверки. Пособие содержит методические указания по теории погрешностей. Работы расположены в последовательности изложения материала курса Общая физика, раздел Механика
 Скачать 0.7 Mb. Скачать 0.7 Mb.
|
Алгоритм вычисления ошибки прямых равноточных измеренийЕсли интересующая нас величина х измерялась непосредственно (прямые измерения) и получены результаты измерений х1, х2, х3,...,хn, то при обработке результатов измерений предлагается следующий порядок операций: Результаты каждого измерения записываются в таблицу. В качестве оценки результата измерения величины х определяется среднее арифметическое из n измерений 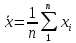 Вычисляется средняя квадратичная погрешность результата серии измерений 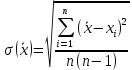 Задается значение надежности α и при данном числе n измерений по табл. 1 приложения определяется коэффициент Стьюдента 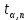 . .Находят границы доверительного интервала для многократных измерений (случайная погрешность серии измерений) 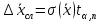 Оценивается доверительный интервал (погрешность) однократного измерения 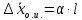 где l - параметр равномерного распределения. В качестве границ доверительного интервала величины х следует взять 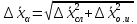 Окончательный результат записывается в виде 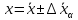 с доверительной вероятностью α. Оценивается относительная погрешность результата измерений 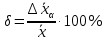 Относительная погрешность позволяет сравнивать неточности измерений различных величин. Ошибки косвенных измеренийВ большинстве физических экспериментов представляет интерес физическая величина, которая не измеряется непосредственно каким- либо прибором, а рассчитывается на основе измерения ряда промежуточных величин. Искомая величина, связана функциональной зависимостью с измеряемыми величинами. В таком случае говорят, что величина измерена косвенным путем или говорят о косвенных измерениях. В этом случае встает задача вычисления погрешности косвенных измерений, если погрешности прямых измерений известны или найдены границы доверительных интервалов величин измеренных методом прямых измерений. При косвенных измерениях значение у измеряемой величины находят по некоторой формуле 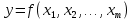 , где , где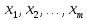 - независимые переменные, для определения которых производятся n прямых независимых измерений. - независимые переменные, для определения которых производятся n прямых независимых измерений.Среднее значение измеряемой величины 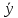 находят по функциональной зависимости, если в нее подставить средние значения переменных находят по функциональной зависимости, если в нее подставить средние значения переменных 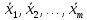 Ошибка (доверительный интервал результата косвенных измерений) величины 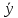 будет равна будет равна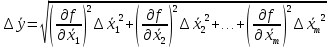 (12) (12)или короче 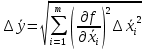 Здесь 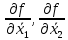 и т.д. – частные производные функции и т.д. – частные производные функции 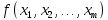 попеременным попеременным 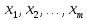 соответственно, подсчитанные при соответственно, подсчитанные при 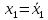 , , 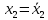 , , 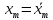 и т.д., а и т.д., а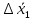 , , 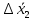 , …, , …, 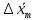 – доверительные интервалы непосредственно измеряемых величин. – доверительные интервалы непосредственно измеряемых величин.Для того что бы проще вычислить погрешность косвенного измерения можно воспользоваться следующими правилами. Правило 1. Квадрат абсолютной погрешности суммы (а также разности) физических величин равен сумме квадратов погрешностей этих величин. Правило 2. Если результат является функцией отношений или произведений нескольких величин, то квадрат относительной погрешности результата равен сумме квадратов относительных погрешностей отдельных измерений. Правило 3. Относительная погрешность степени, т.е. величины 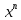 , в n раз больше относительной погрешности величины x. , в n раз больше относительной погрешности величины x.В таблице 2, приведены формулы для погрешностей результата в случае некоторых основных функций. Таблица 2 Погрешности косвенного измерения для основных функций
| |||||||||||||||||||||||||||