|
|
механика_лабораторные работы. Контрольные вопросы для самопроверки. Пособие содержит методические указания по теории погрешностей. Работы расположены в последовательности изложения материала курса Общая физика, раздел Механика
Лабораторная работа №12
МАТЕМАТИЧЕСКИЙ МАЯТНИК
Цель работы: Изучить гармонические колебания на примере движения математического маятника. Определить ускорение свободного падения при помощи математического маятника.
Приборы и принадлежности: Модульный учебный комплекс МУК-М1: рабочий узел «маятник», груз на нити, дополнительные грузы, электронный секундомер СЭ1.
Краткое теоретическое введение
Колебания – движения или процессы, обладающие той или иной степенью повторяемости во времени. Колебания представляют собой один из наиболее распространенных видов движений в природе и технике.
Колебания могут быть разной природы: механические, электромагнитные, электромеханические и другие. В зависимости от характера воздействия на колеблющуюся систему различают: свободные (или собственные), затухающие, вынужденные, а также автоколебания и параметрические колебания.
• Свободными или собственными называются такие колебания, которые происходят в системе, предоставленной самой себе после того, как она была выведена из положения равновесия.
• Вынужденными называются такие колебания, в процессе которых колеблющаяся система подвергается воздействию внешней периодически изменяющейся силы.
• Автоколебания, как и вынужденные колебания, сопровождаются воздействием на колеблющуюся систему внешней силы; однако моменты времени, когда осуществляются эти воздействия, задаются самой колеблющейся системой – система сама управляет внешним воздействием.
• При параметрических колебаниях за счет внешнего воздействия происходит периодическое изменение какого-либо параметра системы.
Простейшим видом колебаний являются гармонические колебания. Это такие колебания, при которых колеблющаяся величина изменяется по закону синуса (или косинуса). Этот вид колебаний особенно важен, так как многие колебания часто имеют характер, очень близкий к гармоническим колебаниям. Периодические процессы иной формы (с другой зависимостью от времени) могут быть представлены как наложение нескольких гармонических колебаний.
Уравнение гармонических колебаний можно представить в виде:
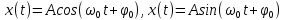 . (1) . (1)
Поскольку косинус изменяется в пределах от -1 до +1, значения x(t) лежат в пределах от -А до +А. Наибольшая величина отклонения от положения равновесия А называется амплитудой колебаний. Амплитуда А – постоянная положительная величина 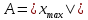 . Аргумент косинуса - величина . Аргумент косинуса - величина 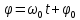 , называется фазой колебаний. , называется фазой колебаний.
Постоянная величина φ0 представляет собой значение фазы в момент времени 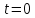 и называется начальной фазой колебаний. С изменением начала отсчета времени изменяется и φ0. Следовательно, значение начальной фазы определяется выбором начала отсчета времени. Так как значения x(t) не изменяется при добавлении или вычитании из фазы целого числа 2π, всегда можно добиться того, чтобы начальная фаза была по модулю меньше π. Поэтому обычно рассматриваются только значения φ0, лежащие в пределах от -π до +π. и называется начальной фазой колебаний. С изменением начала отсчета времени изменяется и φ0. Следовательно, значение начальной фазы определяется выбором начала отсчета времени. Так как значения x(t) не изменяется при добавлении или вычитании из фазы целого числа 2π, всегда можно добиться того, чтобы начальная фаза была по модулю меньше π. Поэтому обычно рассматриваются только значения φ0, лежащие в пределах от -π до +π.
Период гармонического колебания T это такой промежуток времени, за который фаза колебаний получает приращение, равное 2π, т.е. совершается одно полное колебание. По истечении времени Т, соответствующего периоду колебания, движущаяся точка занимает своё прежнее положение. Следовательно, период колебания Т определяется из условия:
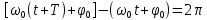
откуда:
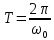 (2) (2)
Величина ω0 - называется собственной циклической частотой гармонических колебаний. Значение ω0 равно числу колебаний за 2π секунд. Величина ν0, обратная периоду колебаний – называется собственной частотой колебаний.
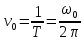 (3) (3)
В качестве примера колебательного движения, поясняющего физические условия, при которых совершаются гармонические колебания, может служить движение математического маятника.
Математическим маятником называют идеализированную систему, состоящую из невесомой и нерастяжимой нити, на одном конце которой прикреплена масса, сосредоточенная в одной точке. Хорошим приближением математического маятника является небольшой тяжелый шарик, подвешенный на тонкой длинной нити, при условии, что радиус шарика много меньше длины нити l. Если маятник отклонить от положения равновесия на небольшой угол α (α – угол, образованный нитью с вертикалью) и отпустить его, то маятник начнет совершать колебательное движение (рис.1).
Получить уравнение колебаний математического маятника можно исходя из закона сохранения энергии. Поскольку маятник совершает только вращательное движение с угловой скоростью ω в поле действия силы тяжести, то можно записать:
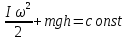 (4) (4)
где I – момент инерции маятника, m – масса маятника, h – высота подъема груза.
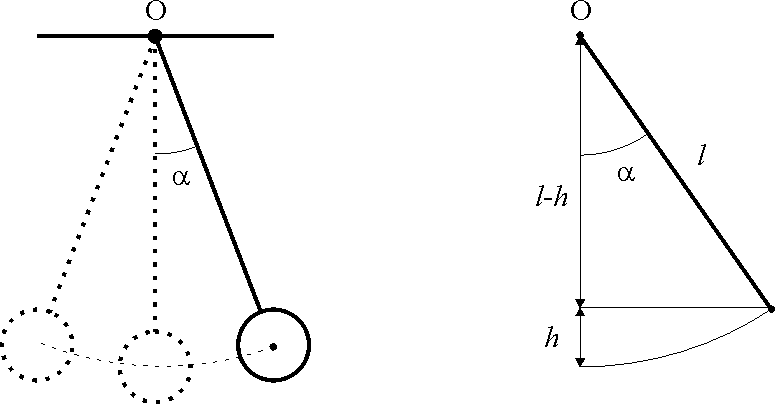
рис. 1
Исходя из рис.1
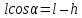 , , 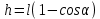 . .
Разложим в ряд до второго члена cos(α) и подставим предыдущее выражение:
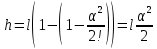
Перепишем выражение (4), продифференцировав части равенства по t:
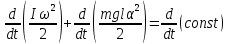
Упростив, получим
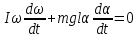
Учитывая, что 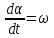 , получим , получим
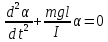 (5) (5)
т.к. для математического маятника 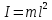 , и обозначив , и обозначив 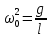 получим: получим:
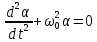 (6) (6)
Решением данного однородного дифференциального уравнения второго порядка является функция:
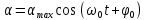 , (7) , (7)
где 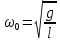 – собственная циклическая частота колебаний математического маятника; – собственная циклическая частота колебаний математического маятника; 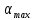 – максимальное значение α; φ0 – начальная фаза. Убедиться в справедливости решения (7) можно путем непосредственной подстановки его в уравнение (6). – максимальное значение α; φ0 – начальная фаза. Убедиться в справедливости решения (7) можно путем непосредственной подстановки его в уравнение (6).
Из предыдущего выражения вытекает, что собственная циклическая частота колебаний математического маятника зависит только от длины маятника и ускорения свободного падения. Учитывая связь между собственной циклической частотой математического маятника и периодом колебаний, получим выражение для периода:
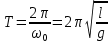 (8) (8)
Таким образом, зная величину l и измерив Т, можно найти ускорение свободного падения.
Методика эксперимента
Определять ускорения свободного падения с помощью математического маятника на практике лучше графическим методом. Для этого необходимо по полученным экспериментальным данным построить график зависимости квадрата периода колебаний маятника от длины нити 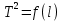 (рис.2). (рис.2).
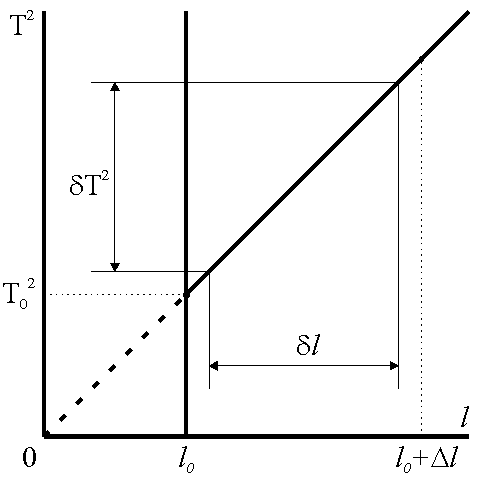
рис. 2
По тангенсу угла наклона полученного графика к оси Т2 можно определить среднюю величину ускорения свободн6ого падения 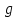 . .
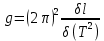 (9) (9)
где δl и δT2 – приращения графика функции 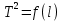 по соответствующим осям. по соответствующим осям.
В реальной лабораторной установке груз это не материальная точка и, следовательно, точное определение длины подвеса невозможно. Поскольку для определения 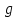 требуется нахождение приращений δl и δT2, то можно перенести начало координат 0 в точку l0, и измерять изменение длины Δl относительно l0 на каждом шаге измерений. Таким образом, построив график зависимости требуется нахождение приращений δl и δT2, то можно перенести начало координат 0 в точку l0, и измерять изменение длины Δl относительно l0 на каждом шаге измерений. Таким образом, построив график зависимости 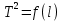 можно найти значение ускорения свободного падения по формуле: можно найти значение ускорения свободного падения по формуле:
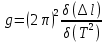 . (10) . (10)
Если продлить характеристику 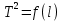 до пересечения с осью Δl то можно найти истинное значение l0. Достоинством этого метода является то, что он позволяет исключить систематическую ошибку в определении длины подвеса. до пересечения с осью Δl то можно найти истинное значение l0. Достоинством этого метода является то, что он позволяет исключить систематическую ошибку в определении длины подвеса.
Все измерения проводятся с помощью модульного учебного комплекса МУК-М1.
Нить наматывается на малый шкив барабана и фиксируется с помощью специального крючка, который расположен на большом шкиву.
Расчет значений приращение длины производить исходя из условия, что минимальная длина подвеса l0 соответствует максимально измеренному значению xmax (рис.3). Таким образом, 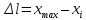 . .
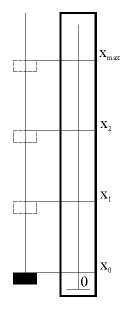
рис. 3
Для проведения измерений необходимо перевести секундомер в режим №3. Выведите груз из положения равновесия на небольшой угол 5 - 10°. Отпустите груз и нажмите кнопку «Пуск» секундомера. Отсчитайте время tизм равное 10 колебаниям и нажмите кнопку «Стоп/Сброс» секундомера. Период колебаний можно рассчитать по формуле 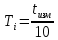 . .
Порядок выполнения работы
Установите минимальное значение массы груза. Установите максимальную длину нити 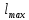 . .
Измерьте время 10 колебаний 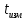 . Вычислите период колебаний T. Данные занесите в таблицу 1. . Вычислите период колебаний T. Данные занесите в таблицу 1.
Увеличивая массу груза, измерьте соответствующие периоды. Убедитесь в том, что период колебаний математического маятника не зависит от массы груза.
Таблица 1
№
|
m, кг
|
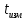 , с , с
|
T
|
1
|
|
|
|
2
|
|
|
|
3
|
|
|
|
Оставьте максимальное значение груза. Уменьшая длину нити на величину 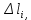 найдите значения найдите значения 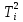 . Проведите 5 измерений. Данные наблюдений запишите в таблицу 2. . Проведите 5 измерений. Данные наблюдений запишите в таблицу 2.
Таблица 2
По результатам измерений постройте график функции 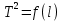 . .
По формуле (10) на линейном участке найдите приращения функций (см. рис.2) и рассчитайте 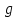 пять раз для разных пар приращений функций. Вычислите среднюю величину. Сравните полученный результат с теоретическим ( пять раз для разных пар приращений функций. Вычислите среднюю величину. Сравните полученный результат с теоретическим (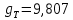 м/с2). м/с2).
Вычислите абсолютную и приведенную погрешность измерения 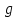 , взяв за , взяв за 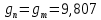 по формулам: по формулам:
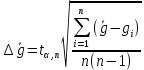
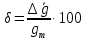
Запишите результат в виде 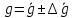
Сделайте выводы.
Контрольные вопросы
Какие колебания называются гармоническими?
Какие виды колебаний вы знаете?
Что такое математический маятник?
К какому виду колебаний относятся колебания маятника в работе?
Чему равен период колебаний математического маятника?
Зависит ли период колебаний математического маятника от массы? Докажите.
Получите уравнение гармонических колебаний математического маятника (6) и его решение (7).
Как определить ускорение свободного падения с помощью математического маятника?
*Предложите методику эксперимента, в котором бы учитывалось затухание колебаний, и имелась возможность расчета декремента затухания колебаний.
|
|
|
 Скачать 0.7 Mb.
Скачать 0.7 Mb.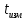 , с
, с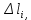 найдите значения
найдите значения 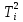 . Проведите 5 измерений. Данные наблюдений запишите в таблицу 2.
. Проведите 5 измерений. Данные наблюдений запишите в таблицу 2.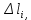
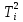
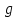
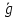
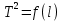 .
.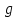 пять раз для разных пар приращений функций. Вычислите среднюю величину. Сравните полученный результат с теоретическим (
пять раз для разных пар приращений функций. Вычислите среднюю величину. Сравните полученный результат с теоретическим (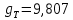 м/с2).
м/с2).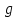 , взяв за
, взяв за 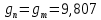 по формулам:
по формулам: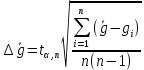
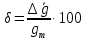
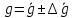

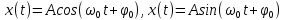 . (1)
. (1)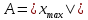 . Аргумент косинуса - величина
. Аргумент косинуса - величина 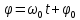 , называется фазой колебаний.
, называется фазой колебаний. 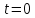 и называется начальной фазой колебаний. С изменением начала отсчета времени изменяется и φ0. Следовательно, значение начальной фазы определяется выбором начала отсчета времени. Так как значения x(t) не изменяется при добавлении или вычитании из фазы целого числа 2π, всегда можно добиться того, чтобы начальная фаза была по модулю меньше π. Поэтому обычно рассматриваются только значения φ0, лежащие в пределах от -π до +π.
и называется начальной фазой колебаний. С изменением начала отсчета времени изменяется и φ0. Следовательно, значение начальной фазы определяется выбором начала отсчета времени. Так как значения x(t) не изменяется при добавлении или вычитании из фазы целого числа 2π, всегда можно добиться того, чтобы начальная фаза была по модулю меньше π. Поэтому обычно рассматриваются только значения φ0, лежащие в пределах от -π до +π.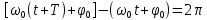
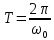 (2)
(2)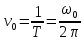 (3)
(3)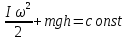 (4)
(4)
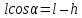 ,
, 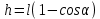 .
. 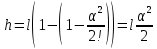
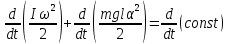
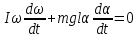
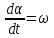 , получим
, получим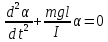 (5)
(5)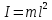 , и обозначив
, и обозначив 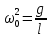 получим:
получим: 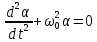 (6)
(6)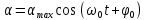 , (7)
, (7)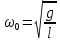 – собственная циклическая частота колебаний математического маятника;
– собственная циклическая частота колебаний математического маятника; 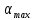 – максимальное значение α; φ0 – начальная фаза. Убедиться в справедливости решения (7) можно путем непосредственной подстановки его в уравнение (6).
– максимальное значение α; φ0 – начальная фаза. Убедиться в справедливости решения (7) можно путем непосредственной подстановки его в уравнение (6).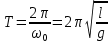 (8)
(8)
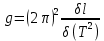 (9)
(9)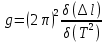 . (10)
. (10)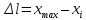 .
.
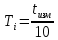 .
.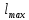 .
.