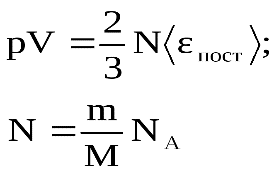Контрольные вопросы к зачету Предмет физики. Связь физики с другими науками и техникой. Характеристики поступательного движения точки

• Название: Контрольные вопросы к зачету Предмет физики. Связь физики с другими науками и техникой. Характеристики поступательного движения точки
• Дата: 10.10.2018
• Размер: 1.81 Mb.
• Имя файла: nurik.docx
• Тип: Контрольные вопросы; #53040
• страница: 3 из 22

20. Основное уравнение молекулярно – кинетической теории идеальных газов и его следствия.

Рассмотрим одноатомный идеальный газ, занимающий некоторый объем V(рис.1.1.) Пусть число столкновений между молекулами пренебрежимо мало по сравнению с числом столкновений со стенками сосуда. В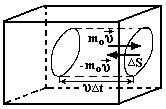



Рис.1.1. К выводу основного уравнения молекулярно-кинетической теории.

ыделим на стенке сосуда некоторую элементарную площадку ΔSи вычислим давление, оказываемое на эту площадку. При каждом соударении молекула, массойm₀, движущаяся перпендикулярно площадке со скоростьюυ, передает ей импульс, который представляет собой разницу импульсов молекулы до и после соударения:

m₀υ-(-m₀υ) = 2m₀υ.

За время Δtплощадки ΔSдостигнут только те молекулы, которые заключены в объеме цилиндра с основанием ΔSи длинойυΔt. Это число молекул будетnυΔSΔt, гдеn– концентрация молекул. Необходимо, однако, учитывать, что реально молекулы движутся к площадке под разными углами и имеют различные скорости, причем скорость молекул при каждом соударении меняется. Для упрощения расчетов хаотическое движение молекул заменяют движением вдоль трех взаимно перпендикулярных координатных осей, так что в любой момент времени вдоль каждого из них движется 1/3 молекул, причем половина – 1/6 – движется в одну сторону, половина – в противоположную. Тогда число ударов молекул, движущихся в заданном направлении, о площадку ΔSбудетnυΔSΔt/6. При столкновении с площадкой эти молекулы передадут ей импульс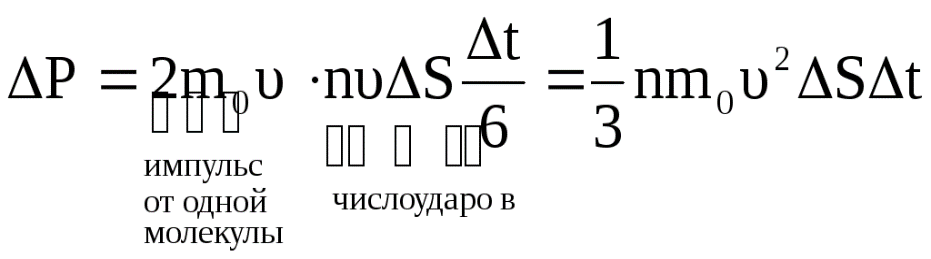

.

В данном случае, когда сила, действующая на единицу площади, постоянна, для давления газа на стенку сосуда мы можем записать р = F/ΔS= ΔP/ΔSΔt= =nm₀υ²/3. Молекулы в сосуде движутся с самыми различными скоростямиυ_1,υ_2….υ_n,общее число их –N. Поэтому необходимо рассматривать среднюю квадратичную скорость, которая характеризует всю совокупность молекул:

Таким образом, давление газа, оказываемое им на стенку сосуда, будет равно

Приведенное выше уравнение и есть основное уравнение молекулярно-кинетической теории идеальных газов. Посколькуm₀‹υ_кв›²/2 – это средняя энергия поступательного движения молекулы ‹ ε_пост›, уравнение можно переписать в виде:

Следствия:

1. Учитывая, что концентрация n=N/V, получаем

гдеE– суммарная кинетическая энергия поступательного движения всех молекул газа. Таким образом, давление равно двум третям энергии поступательного движения молекул, содержащихся в единице объема газа.

2. Для вывода второго следствия воспользуемся первым следствием и уравнением Менделеева-Клапейрона: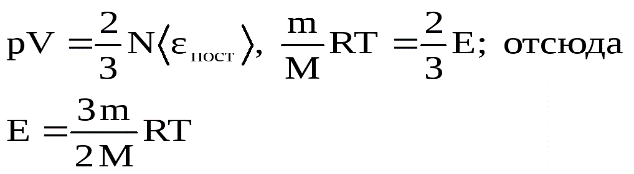

Энергия молекул Е в веществе пропорциональна количеству вещества в системе и температуре.

4. 
   Найдем еще кинетическую энергию поступательного движения одной молекулы ‹ε_пост›, учитывая
   

k=R/N_Aполучим:

Отсюда следует, что средняя кинетическая энергия хаотического поступательного движения молекул идеального газа пропорциональна его абсолютной температуре и зависит только от нее, т.е. температура есть количественная мера энергии теплового движения молекул.При одинаковой температуре средние кинетические энергии молекул любого газа одинаковы. При Т=0К ‹ε_пост› = 0 и поступательное движение молекул газа прекращается, однако анализ различных процессов показывает, что Т = 0К – недостижимая температура.

4. Учитывая, что ‹ε_пост› = 3kT/2, р = 2n‹ε_пост›/3, получим отсюда: р =nkT.

Мы получили уже знакомый нам вариант уравнения Менделеева-Клапейрона, выведенный в данном случае из понятий молекулярно-кинетической теории статистическим методом. Последнее уравнение означает, что при одинаковых температуре и давлении все газы содержат в единице объема одинаковое число молекул.