Контрольные вопросы к зачету Предмет физики. Связь физики с другими науками и техникой. Характеристики поступательного движения точки
 Скачать 1.81 Mb.
|
24. Среднее число столкновений и длина свободного пробега молекул.16. 1. Длина свободного пробега молекул.Длиной свободного пробега называется путь, проходимый молекулой между двумя последовательными столкновениями. Вследствие хаотичности движения различны. Средней длиной свободного пробега молекул <>называется путь, который в среднем проходят молекулы между двумя последовательными столкновениями:
где N - число молекул.
Значения D при нормальных условиях для некоторых газов
16. 2. Среднее число столкновений молекул.Введём понятие среднего числа столкновений <>молекулы в единицу времени. Тогда число столкновений молекулы за время есть  и оно равно отношению среднего пути молекулы  к средней длине свободного пробега <>:
Введём понятие эффективного сечения столкновения как площади поперечного сечения («коридора») ломаного цилиндра, в которой должны попасть центры соседних молекул, чтобы столкнуться с данной. Из рисунка 16.2 видно, что:
Рассчитаем число столкновений молекулы за время . Предположим, что рассматриваемая молекула движется со скоростью  , а остальные покоятся. Тогда рассматриваемая молекула столкнётся со всеми молекулами, находящимися в цилиндре площадью основания Sэфф и длиной  . Число молекул, а значит и число столкновений определяется соотношением:
где n- концентрация молекул. Чтобы учесть движение всех молекул можно, например, перейти в систему координат, связанную с движущейся молекулой, т.е. перейти от скорости к средней скорости движения молекул. Поскольку все движения молекул равновероятны, то угол между направлениями скоростей лежит в интервале ( ) и средний угол равен  . Модуль относительной скорости тогда будет:
С учётом сделанных поправок, формула () приобретает вид:
Тогда среднее число столкновений молекулы в единицу времени  будет определяться выражением:
Приведённое соотношение носит название формулы Клаузиуса - Максвелла. Чтобы найти число столкновений в единицу времени молекул газа концентрации и в объёме , т.е. для  молекул газа надо величину умножить на  , т.к. в каждом столкновении принимают участие 2 молекулы:
Тогда среднее число столкновений молекул в единицу времени в единичном объёме есть:
Теперь можно вернуться к средней длине свободного пробега молекулы. За время молекула проходит путь:
и испытывает за это время число соударений, равное:
Значит средняя длина свободного пробега  будет равна (с учётом ()):
Если учесть, что  , то получаем:
Концентрация молекул связана с термодинамическими параметрами и уравнением состояния.
Тогда окончательно получаем:
25.
В неравновесных системах возникают особые необратимые процессы, называемые явлениями переноса, в результате которых происходит пространственный перенос массы, энергии, импульса. Диффузия обусловлена переносом массы, теплопроводность – переносом энергии, а вязкость – переносом импульса. Для характеристики необратимых процессов переноса вводятся параметры теплового движения молекул: среднее число соударений молекулы в единицу времени и средняя длина свободного пробега молекул . Среднее число соударений молекулы за 1 с :  ,где d – эффективный диаметр молекул, т.е. минимальное расстояние, на которое сближаются при столкновении центры двух молекул, – эффективное сечение молекул, – концентрация молекул, – средняя арифметическая скорость молекул. Средняя длина свободного пробега молекул , т.е. средний путь, проходимый молекулой между двумя последовательными столкновениями: 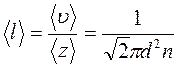 .При рассмотрении одномерных явлений переноса система отсчета выбирается так, чтобы ось х была ориентирована в направлении переноса. 1. Диффузия. Явление диффузии заключается в том, что происходит самопроизвольное взаимопроникновение и перемешивание частиц двух соприкасающихся газов, жидкостей и даже твердых тел. Диффузия сводится к переносу массы, возникает и продолжается до тех пор, пока на границе соприкосновения двух сред градиент плотности отличен от нуля. Градиент плотности вдоль выбранной оси х, перпендикулярной плоскости соприкосновения двух сред, обозначается как и показывает как быстро изменяется величина плотности от точки к точке вдоль оси х. Количественно явление диффузии подчиняется закону Фика: 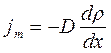 ,где – плотность потока массы, то есть величина, определяемая массой газа, диффундирующего через единичную площадку S в единицу времени, – градиент плотности газа в направлении x, перпендикулярном выбранной площадке S , D – коэффициент диффузии. Знак минус в приведенной формуле означает, что перенос массы происходит в направлении убывания плотности. Согласно молекулярно-кинетической теории идеального газа, коэффициент диффузии D: 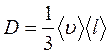 ,где – средняя скорость теплового движения молекул, – средняя длина свободного пробега молекул. 2. Теплопроводность. Если в одной области газа температура больше,чем в другой, то с течением времени вследствие постоянных столкновений молекул происходит процесс выравнивания средних кинетических энергий молекул, то есть процесс выравнивания температуры. Этот процесс переноса энергии, называемый теплопроводностью, возникает и продолжается до тех пор, пока на границе соприкосновения двух частей газа градиент температуры отличен от нуля. Градиент температуры Т газа вдоль выбранной оси х, перпендикулярной плоскости соприкосновения двух частей газа, имеющих различную температуру, обозначается как и показывает как быстро изменяется температура газа от точки к точке вдоль оси х. Количественно теплопроводность подчиняется закону Фурье: 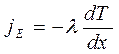 ,где– плотность теплового потока, определяемая энергией, переносимой в форме теплоты через единичную площадку S в единицу времени, – градиент температуры в направлении x, перпендикулярном выбранной площадке S, – коэффициент теплопроводности. Знак минус в приведенной формуле означает, что при теплопроводности энергия переносится в направлении убывания температуры. Согласно молекулярно-кинетической теории идеального газа, коэффициент теплопроводности: 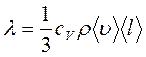 ,где – удельная теплоемкость газа при изохорном процессе (количество теплоты, необходимое для изохорного нагревания 1 кг газа на 1 К), – плотность газа, – средняя скорость теплового движения молекул, – средняя длина свободного пробега молекул. 3. Вязкость. Вязкость это свойство жидкости или газа, обусловленное внутренним трением между соприкасающимися параллельными слоями жидкости или газа, движущимися с различными скоростями. В результате, импульс слоя, движущегося быстрее, уменьшается, а движущегося медленнее – увеличивается, что приводит к торможению слоя, движущегося быстрее, и ускорению слоя, движущегося медленнее. Другими словами, внутреннее трение приводит к переносу импульса от одного движущегося слоя жидкости или газа к другому соприкасающемуся с ним слою. Количественно сила внутреннего трения между двумя соприкасающимися слоями жидкости или газа подчиняется закону Ньютона: 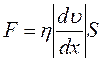 ,где h – коэффициент динамической вязкости, – градиент скорости, показывающий быстроту изменения скорости течения жидкости или газа от слоя к слою в направлении х,перпендикулярном направлению движения слоев, S – площадь соприкосновения слоев жидкости или газа, на которые действует сила внутреннего трения F. Закон Ньютона для внутреннего трения можно представить в виде: 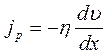 ,где – плотность потока импульса – величина, определяемая импульсом, переносимым в единицу времени через единичную площадку Sсоприкосновения слоев жидкости или газа в направлении оси х, перпендикулярном направлению движения слоев жидкости или газа. Знак минус в приведенной формуле означает, что импульс переносится от слоя к слою жидкости (газа) в направлении убывания скорости их движения. Согласно молекулярно-кинетической теории идеального газа, коэффициент динамической вязкости идеального газа h определяется следующим образом: 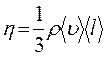 ,где – плотность газа, – средняя скорость теплового движения молекул, – средняя длина свободного пробега молекул. 26. Основы термодинамики Термодинамика изучает процессы и явления, происходящие в природе и технике, с точки зрения преобразования энергии, в том числе внутренней энергии тел. Термодинамическая система – это совокупность тел, способных обмениваться энергией между собой и с другими системами. Замкнутая термодинамическая система не обменивается энергией с другими системами. Каждое тело имеет вполне определенную структуру, оно состоит из частиц, которые хаотически движутся и взаимодействуют друг с другом, поэтому любое тело обладает внутренней энергией. Внутренняя энергия — это величина, характеризующая собственное состояние тела, т. е. энергия хаотического (теплового) движения микрочастиц системы (молекул, атомов, электронов, ядер и т. д.) и энергия взаимодействия этих частиц. Внутренняя энергия идеального газа складывается только из энергии движения молекул, так как взаимодействием молекул можно пренебречь. Внутренняя энергия одноатомного идеального газа определяется по формуле U = 3/2 • m/М • RT. Внутренняя энергия одного моля одноатомного идеального газа:
Внутреннюю энергию можно изменить двумя способами: путем теплопередачи и путем совершения механической работы Теплопередача — это изменение внутренней энергии без совершения работы: энергия передается от более нагретых тел к менее нагретым. Теплопередача бывает трех видов: теплопроводность (непосредственный обмен энергией между хаотически движущимися частицами взаимодействующих тел или частей одного и того же тела); конвекция (перенос энергии потоками жидкости или газа) и излучение (перенос энергии электромагнитными волнами). Мерой переданной энергии при теплопередаче является количество теплоты (Q). Принято считать, что Q > 0, если тело получает энергию, и Q < 0, если тело отдает свою энергию При совершении механической работы должно происходить направленное перемещение тел под действием сил, например, перемещение поршня в цилиндре с газом. Если газ расширяется, то сила давления газа на поршень совершает положительную работу (A > 0) за счет внутренней энергии газа. Если внешние силы больше силы давления газа, то газ сжимается и работа газа будет отрицательной (A < 0), при этом внутренняя энергия увеличивается. При изобарном нагреваниигаз совершает работу над внешними силами 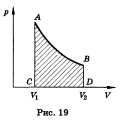 , где V1 и V2 — начальный и конечный объемы газа. Если процесс не является изобарным, величина работы может быть определена площадью фигуры ABCD, заключенной между линией, выражающей зависимость p(V), и начальным и конечным объемами газа V  Первый закон термодинамики : изменение внутренней энергии замкнутой системы равно сумме количества теплоты, переданной системе, и работы внешних сил, совершенной над системой.  ,где — изменение внутренней энергии, Q — количество теплоты, переданное системе, А — работа внешних сил. А*-работа самой системы, т.е.работа газа. Если система сама совершает работу и получает или отдает теплоту, то изменение ее внутренней энергии∆U = Q – A. Применение первого закона термодинамики к изопроцессам В изотермическом процессе температура постоянная, следовательно, внутренняя энергия не меняется. Тогда уравнение первого закона термодинамики примет вид:  , т. е. количество теплоты, переданное системе, идет на совершение работы при изотермическом расширении, именно поэтому температура не изменяется. В изобарном процессегаз расширяется и количество теплоты, переданное газу, идет на увеличение его внутренней энергии и на совершение им работы:  . При изохорном процессе газ не меняет своего объема, следовательно, работа им не совершается, т. е. А = 0, и уравнение первого закона имеет вид  , т. е. переданное количество теплоты идет на увеличение внутренней энергии газа. Адиабатным называют процесс, протекающий без теплообмена с окружающей средой. Q = 0, следовательно, газ при расширении совершает работу за счет уменьшения его внутренней энергии, следовательно, газ охлаждается,  Второе начало термодинамики гласит, что невозможен самопроизвольный переход тепла от тела, менее нагретого, к телу, более нагретому. |
,
.
,
.
.
.
.
.
,
.
.
.
.
.