Контрольные вопросы к зачету Предмет физики. Связь физики с другими науками и техникой. Характеристики поступательного движения точки

• Название: Контрольные вопросы к зачету Предмет физики. Связь физики с другими науками и техникой. Характеристики поступательного движения точки
• Дата: 10.10.2018
• Размер: 1.81 Mb.
• Имя файла: nurik.docx
• Тип: Контрольные вопросы; #53040
• страница: 4 из 22

21. Закон равномерного распределения энергии по степеням свободы

Напомним, что под числом степеней свободы тела понимают наименьшее число независимых координат, необходимых для полного определения положения тела.

Л. Больцман установил закон равномерного распределения энергии молекул идеального газа по степеням свободы: на каждую степень свободы молекулы в среднем приходится одинаковая кинетическая энергия, равная kT/2.

Таким образом, молекула с i-степенями свободы обладает средней кинетической энергией, равной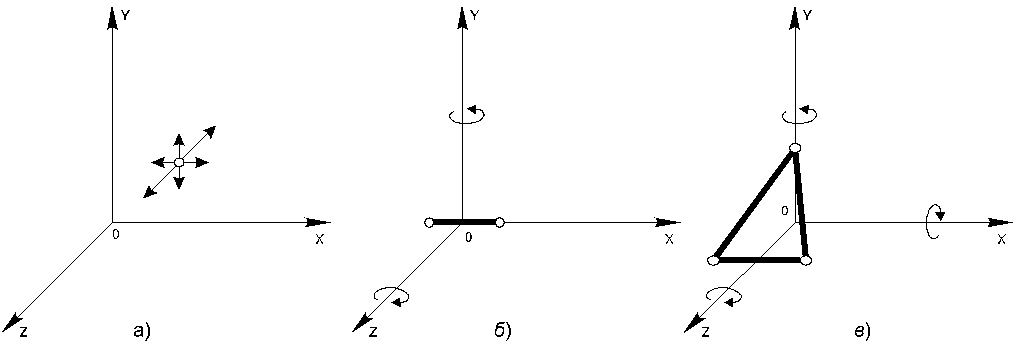



Рис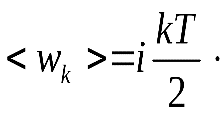.20.1

(20.1)

Заметим, что при определении числа степеней свободы молекул газов принимаются во внимание те степени свободы, которые вносят существенный вклад в ее кинетическую энергию.

Например, молекула одноатомного газа, принимаемая за материальную точку (рис.20.1.а) и способная совершать три независимых движениях (вдоль осей X, Y и Z), имеет три степени свободы. Следовательно, средняя кинетическая энергия такой молекулы . Этот вывод согласуется с выражением (15.25). Действительно, ввиду хаотичности теплового движения молекул кинетическая энергия каждой из них равномерно распределяется между тремя степенями свободы, так что в среднем на каждую степень свободы приходится энергия, равнаяkT/2.

Молекулу двухатомного газа можно представить в виде двух атомов, жестко связанных друг с другом (рис.20.1.б). Кроме трех степеней свободы поступательного движения, такая система имеет еще две степени свободы вращения вокруг осей Y и Z(вращение вокруг третьей оси X не вносит вклада в энергию молекулы, так как момент инерции молекулы относительно этой оси ничтожно мал). Таким образом, двухатомная молекула имеет пять степеней свободы и, следовательно, обладает средней кинетической энергией .

Молекулы, состоящие из трех и более атомов, имеют шесть степеней свободы: три поступательных и три вращательных (рис.20.1.в). Для таких молекул .

Строго говоря, связи между атомами в молекулах реальных газов не являются абсолютно жесткими, поэтому при некоторых условиях (например, при повышенных температурах) эти связи скорее можно представить в виде упругих пружин, результатом чего являются дополнительные, колебательные степени свободы.

Закон равномерного распределения энергии по степеням свободы приводит к выводу о равноправности всех степеней свободы молекулы: все они вносят одинаковый вклад в ее среднюю кинетическую энергию.Однако этот вывод имеет ограниченную область применимости и уточнен в квантовой статистике.

22. . Барометрическая формула. Закон Больцмана

Хаотические молекулярные движения приводят к тому, что частицы газа равномерно распределяются по объему сосуда, так что в каждой единице объема содержится в среднем одинаковое число частиц. В равновесном состоянии давление и температура газа также одинаковы во всем объеме. Но так обстоит дело только в том случае, когда на молекулы не действуют внешние силы. При наличии же таких сил молекулярные движения приводят к своеобразному поведению газов.

Рассмотрим, например, газ (воздух), находящийся под действием силы тяжести. Если бы отсутствовало тепловое движение молекул, то все они под действием силы тяжести «упали» бы на Землю, и весь воздух собрался бы тончайшим слоем у поверхности Земли.

Если бы отсутствовала сила тяжести, но существовали бы молекулярные движения, молекулы разлетелись бы по всему мировому пространству. Атмосфера, воздушная оболочка Земли, обязана своим существованием в ее теперешнем виде наличию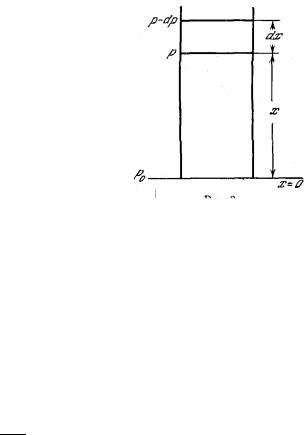

96	Молекулярная физика

одновременно и теплового движения молекул, и силы притяжения к Земле. При этом в атмосфере устанавливается вполне определенное распределение молекул по высоте. Соответственно этому распределению молекул устанавливается и определенный закон изменения давления газа с высотой.

Рассмотрим вертикальный столб воздуха (рис.). Пусть у поверхности Земли, где х = 0, давление равнор0, а на высоте х равно р. При изменении , высоты наdx давление изменяется на

dp.

Давление воздуха на некоторой высоте равно весу вертикального столба воздуха, находящегося на этой высоте над площадью, равной единице. Поэтому dp равно разности весов столбов воздуха над площадью, равной единице, нр высотах х и х + dx,

т. е. равно весу столба воздуха высотой dx с площадью основания в одну единицу:

dp=−ρ gdx,'

где ρ — плотность воздуха (масса единицы объема) и g — ускорение

силы тяжести. Плотность ρ газа равна произведению массыm молекулы на их числоn в единице объема:

ρ=m n.

Из кинетической теории известно, что

p=nkT

Следовательно,

ρ= mk Tp

Тогда

dp=− mgkT p dx

или

dpp=− mgkTdx

Если считать, что температура на всех высотах одна и та же (что, вообще говоря, неверно), то, интегрируя это уравнение, получим:

ln p=−mgkT x+lnC p=C exp(−mgkT x)

где С — постоянная интегрирования.

Постоянная С определяется из условия, что при х=0 давление р =р0. Подставив в уравнение эти значения х и р, получим:

C=p0

97

Молекулярная физика

μ

p=p0 exp(−mgkT x)

учитывая, что m=

(где μ — масса моля, NA — число Авогадро), получаем:

N A

p=p0 exp(−

μ g

x)=p0 exp(−

μ g

x)

k N A T

R T

Это уравнение, устанавливающее закон убывания давления с высотой, называется барометрической формулой. Из этого уравнения видно, что давление газа убывает с высотой по экспоненциальному закону. Этим законом пользуются для определения высоты над Землей путем измерения давления на данной высоте и на уровне моря

Приборы, служащие для измерения высоты горных вершин, полета самолета и т. д., представляют собой специальные барометры, шкала которых проградуирована непосредственно в метрах.

Так как давление газа, как мы видели раньше, пропорционально числу молекул п в единице объема (р = nkT), то барометрическая формула выражает также закон убывания плотности молекул с высотой:

n=n0 exp(−RμTg x)

где n и n0 — число молекул в единице объема в точках, между которыми разность высот равна х. Эта формула показывает, что атмосфера Земли должна простираться до бесконечности.

Однако мы не учли два обстоятельства:

1)температура с высотой меняется

2)атмосфера — неравновесная система.

Тем не менее этой формулой можно пользоваться до высот 60-70км, учитывая оправки на то, что температура меняется с высотой.

Закон Больцмана

Полученная выше барометрическая формула относится к случаю, когда газ находится под действием силы тяжести. Величина mgx в формуле

(− m gx )

n=n0 ek T

представляет собой потенциальную энергию молекулы на высоте х. Можно поэтому сказать, что эта формула дает нам число частиц n, энергия которых

U = mgx,

если число частиц с энергией, равной нулю, равно n0 (высота х отсчитывается от нуля). Нет никаких оснований считать, что поведение газа существенно изменится, если вместо силы тяжести на него будет действоватькакая-либодругая сила, а выражение для энергии будет иметь другой вид. Если газ находится вкаком-нибудьсиловом поле, так что его частицы обладают некоторой потенциальной энергией, то число частиц, обладающих заданной энергией U, определяется формулой

n=n0 e(−	U		)	(1)
kT
98		Молекулярная физика

Эта формула называется формулой Больцмана, Она позволяет определить долю частиц, которые в условиях теплового равновесия обладают энергией U:

Из формулы (1) видно, что доля n/n0 частиц с данной энергией U, кроме величины этой энергии, зависит только от температуры.

Это позволяет трактовать и самую температуру несколько иначе, а именно как величину, от которой зависит, как распределяются частицы по энергиям.

При данной температуре доля молекул, обладающих той или иной энергией U, зависит от значения U и быстро уменьшается с ростом U. Это значит, что доля молекул с очень большой энергией всегда очень мала. И чем ниже температура, тем быстрее n/n0убывает с ростом U.