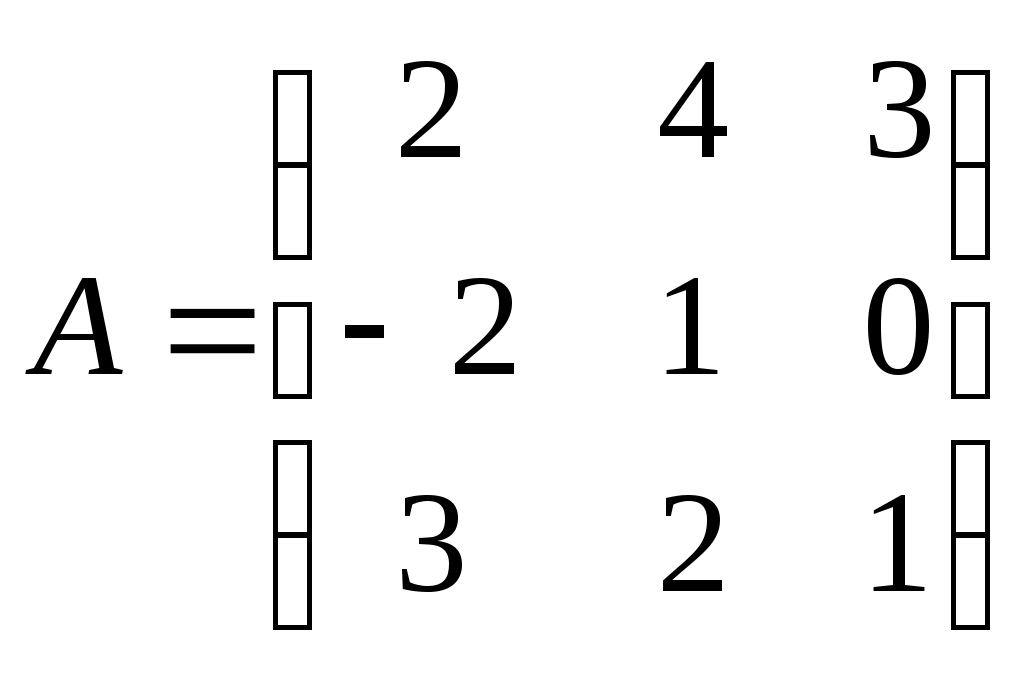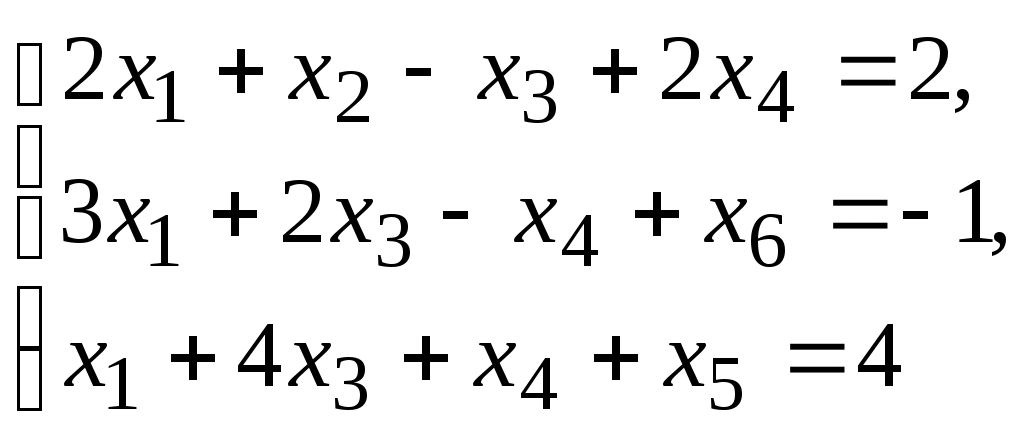КР ро Линейной Алгебре. Решение по линал. Контрольное задание по линейной алгебре и аналитической геометрии
 Скачать 314.5 Kb.
|
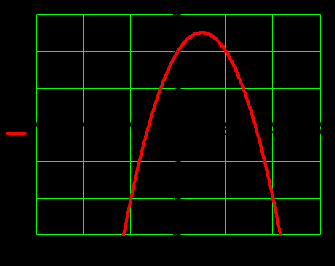
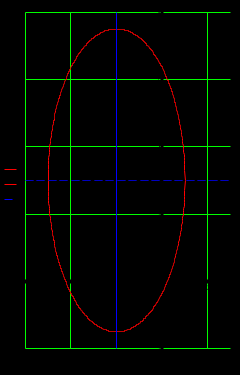
Контрольное задание по линейной алгебре и аналитической геометрииВариант для контрольного задания студент выбирает в соответствии с последней цифрой номера (шифра) своей зачетной книжки. Если шифр заканчивается нулем, то выполняется вариант 10. Каждый вариант состоит из десяти типовых заданий. Приводим описание заданий. Задание 1. Найти произведение заданных матриц А и В. Задание 2. Решить систему линейных алгебраических уравнений по формулам Крамера, матричным методом и методом Гаусса. Задание 3. Показать, что векторы а1, а2, а3 образуют базис в пространстве R3, и найти координаты вектора а в этом базисе. Задание 4. Определить ранг заданной матрицы. Задание 5. Привести систему к системе с базисом методом Жордана-Гаусса и найти одно базисное решение. Задание 6. Найти два опорных решения канонической системы уравнений. Задание 7. Найти собственные значения и собственные векторы данной матрицы. Задание 8. Даны вершины треугольника АВС. Найти уравнения его сторон и точку пересечения высот. Задание 9. Привести уравнение кривой второго порядка к каноническому виду и построить линию. Задание 10. Построить график заданной кривой. Вариант 3Задание 1. Найти произведение заданных матриц А и В. 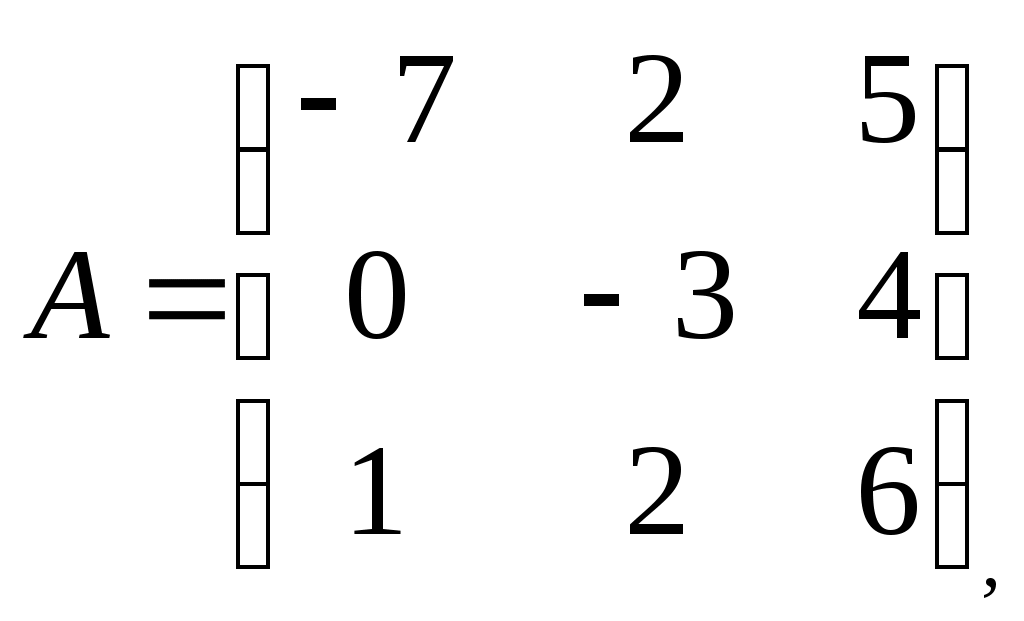 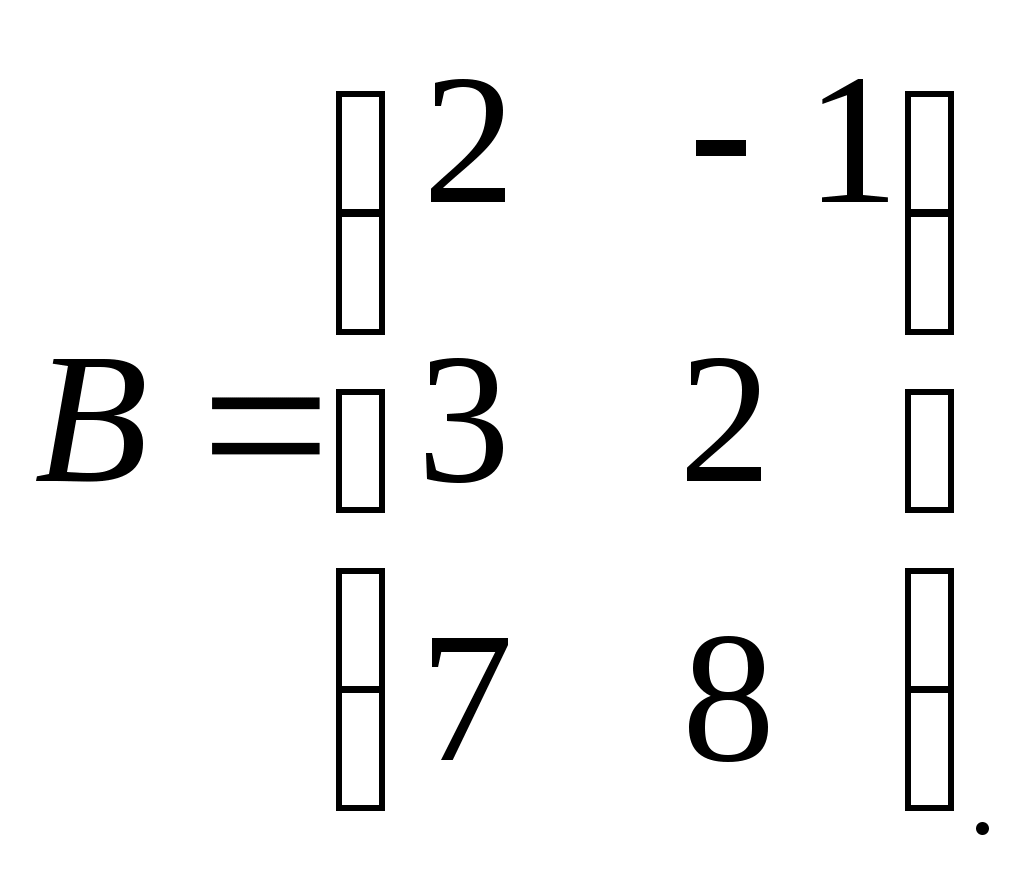 .Решение Так как количество столбцов матрицы А равно количеству строк матрицы В, то произведение А на В существует. Тогда 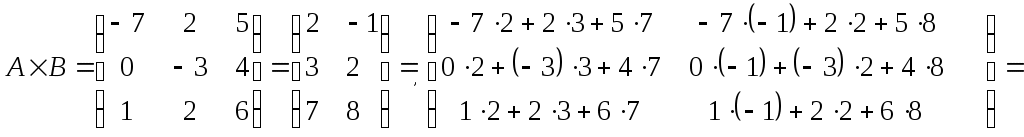 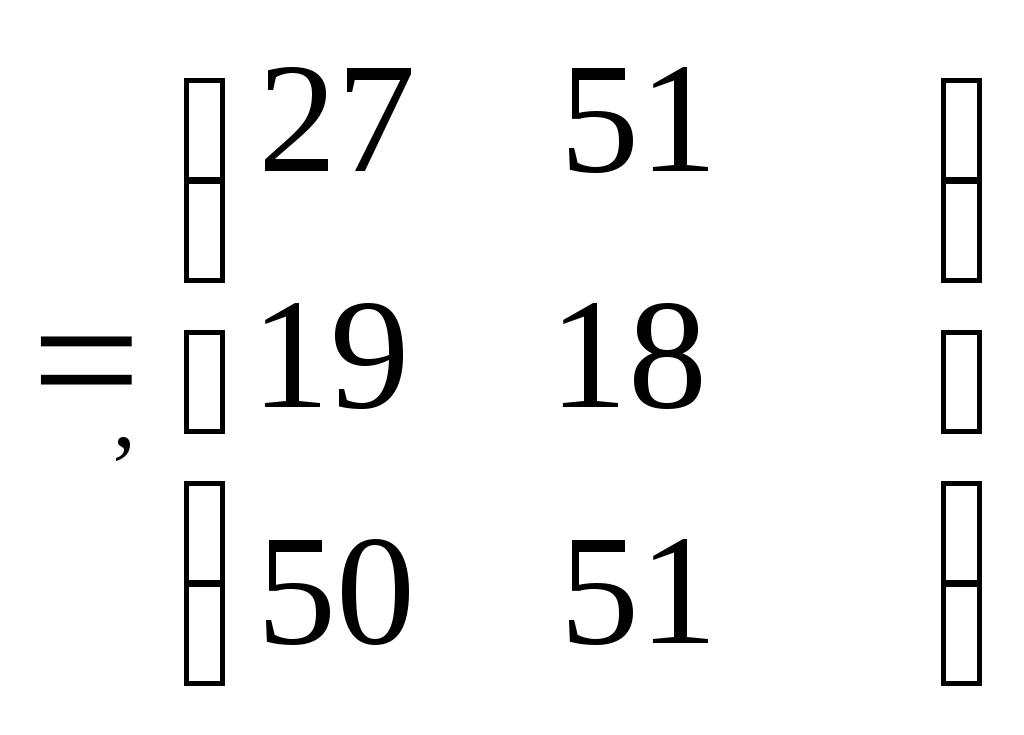 .Искомая матрица имеет размерность 3х2. Задание 2. Решить систему линейных алгебраических уравнений по формулам Крамера, матричным методом и методом Гаусса.  Решение методом Крамера. Система совместна тогда и только тогда, когда системный (главный) определитель не равен нулю. Главный определитель: ∆ = 2 • (1 • 3-(-5) • 2)-4 • (4 • 3-(-5) • (-1))+(-2) • (4 • 2-1 • (-1)) = -20 Заменим 1-ый столбец матрицы А на вектор результата В.
Найдем определитель полученной матрицы. ∆1 = (-1)1 + 1a11∆11 + (-1)2 + 1a21∆21 + (-1)3 + 1a31∆31 = = (-8) • (1 • 3-(-5) • 2)-14 • (4 • 3-(-5) • (-1))+18 • (4 • 2-1 • (-1)) = -40  Заменим 2-ый столбец матрицы А на вектор результата В.
Найдем определитель полученной матрицы. ∆2 = (-1)1 + 1a11∆11 + (-1)2 + 1a21∆21 + (-1)3 + 1a31∆31 = = 2 • (14 • 3-18 • 2)-4 • ((-8) • 3-18 • (-1))+(-2) • ((-8) • 2-14 • (-1)) = 40  Заменим 3-ый столбец матрицы А на вектор результата В.
Найдем определитель полученной матрицы. ∆3 = (-1)1 + 1a11∆11 + (-1)2 + 1a21∆21 + (-1)3 + 1a31∆31 = = 2 • (1 • 18-(-5) • 14)-4 • (4 • 18-(-5) • (-8))+(-2) • (4 • 14-1 • (-8)) = -80  Проверка. 2•2+4•(-2)-1•4 = -8 4•2+1•(-2)+2•4 = 14 -2•2-5•(-2)+3•4 = 18 Ответ:  Решение матричным методом Запишем систему в виде  ,где А – матрица коэффициентов при неизвестных, Х – вектор-столбец неизвестных, В – вектор-столбец свободных коэффициентов. Тогда решение системы в матричном виде получаем в виде:  где А-1 – обратная матрица. где Aij — алгебраическое дополнение элемента aij в определителе матрицы А, которое является произведением (—1)i+j на минор (определитель) n-1 порядка, полученный вычеркиванием i-й строки и j-го столбца в определителе матрицы А. Транспонированная матрица к матрице A имеет вид: Вычисляем алгебраические дополнения. ∆1,1=(1•3-2•(-5))=13 ∆1,2=-(4•3-(-1•(-5)))=-7 ∆1,3=(4•2-(-1•1))=9 ∆2,1=-(4•3-2•(-2))=-16 ∆2,2=(2•3-(-1•(-2)))=4 ∆2,3=-(2•2-(-1•4))=-8 ∆3,1=(4•(-5)-1•(-2))=-18 ∆3,2=-(2•(-5)-4•(-2))=2 ∆3,3=(2•1-4•4)=-14 Из полученных алгебраических дополнений составим присоединенную матрицу C: Вычислим обратную матрицу: Вектор результатов X X=A-1 • B 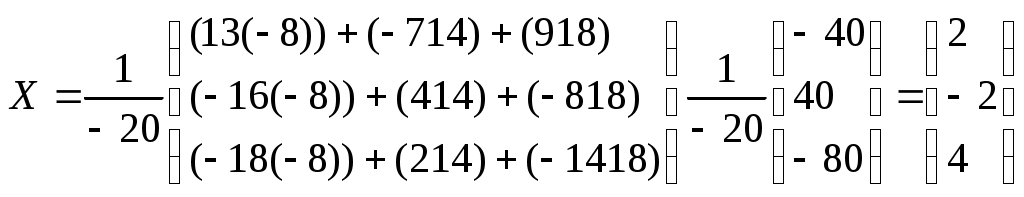 Решение совпадает с полученным методом Крамера. Решение методом Гаусса Запишем систему в виде расширенной матрицы:  Для удобства вычислений поменяем строки местами:  Работаем со столбцом №1 Добавим 3ю строку к 2й:
Умножим 1ю строку на (k = -2 / 4 = -1/2) и добавим к 2й:
Работаем со столбцом №2 Умножим 2ю строку на (k = 1 / 7/2 = 2/7) и добавим к 3й:
Получим единицы на главной диагонали. Для этого всю строку делим на соответствующий элемент главной диагонали:  Теперь исходную систему можно записать как: x1 = 7/2 - (1/4x2 + 1/2x3) x2 = -30/7 - ( - 4/7x3) x3 = 4 Из 3й строки выражаем x3 Из 2й строки выражаем x2 Из 1й строки выражаем x1 Задание 3. Показать, что векторы а1, а2, а3 образуют базис в пространстве R3, и найти координаты вектора а4 в этом базисе. 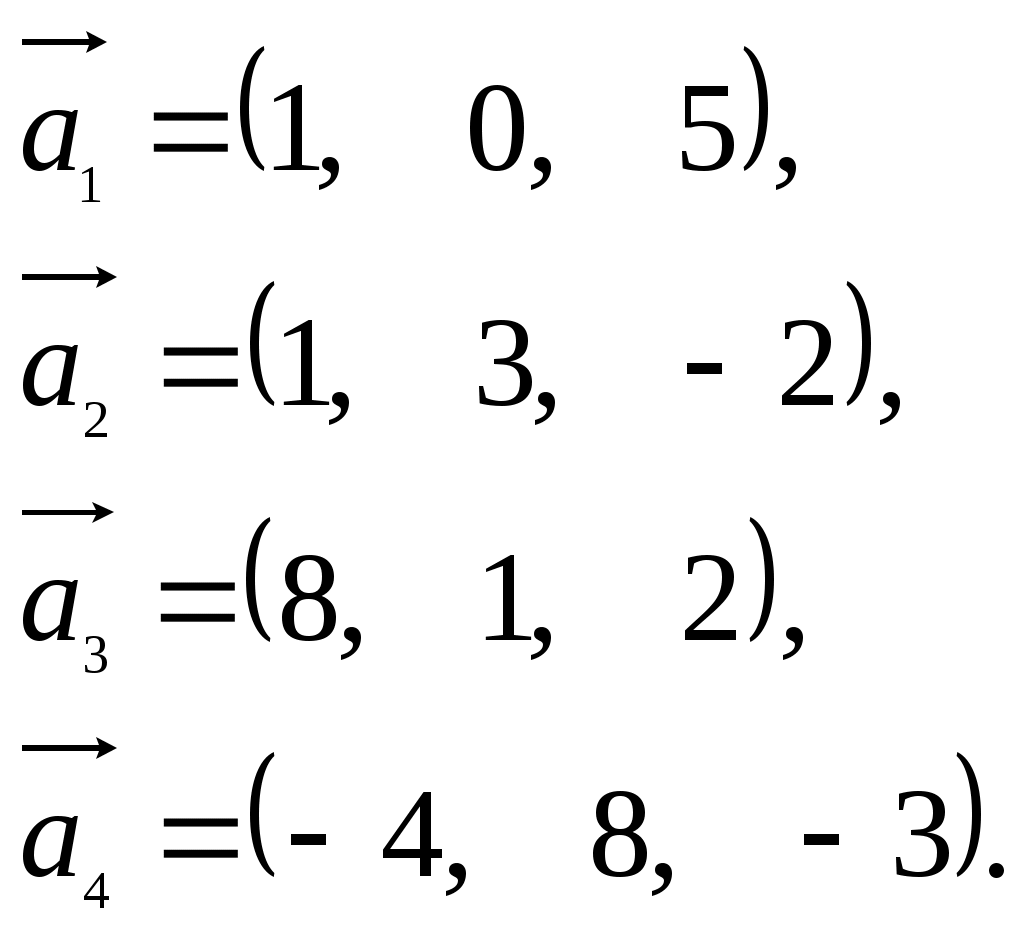 Решение Векторы образуют базис, если определитель, составленный из координат этих векторов, отличен от нуля, в противном случае вектора не являются базисными и вектор X нельзя разложить по данному базису. Вычислим определитель матрицы:
∆ = 1*(3*2 - 1*(-2)) - 1*(0*2 - 1*5) + 8*(0*(-2) - 3*5) = -107. Так как определитель отличен от нуля, то векторы образуют базис, следовательно, вектор X можно разложить по данному базису. Т.е. существуют такие числа α1, α2, α3, что имеет место равенство: X = α1а1 + α2а2 + α3а3 Запишем данное равенство в координатной форме: (-4;8;-3) = α1(1;0;5) + α2(1;3;-2) + α3(8;1;2) Используя свойства векторов, получим следующее равенство: (-4;8;-3) = (1α1;0α1;5α1;) + (1α2;3α2;-2α2;) + (8α3;1α3;2α3;) (-4;8;-3) = (1α1 + 1α2 + 8α3;0α1 + 3α2 + 1α3;5α1 -2α2 + 2α3) По свойству равенства векторов имеем: 1α1 + 1α2 + 8α3 = -4 0α1 + 3α2 + 1α3 = 8 5α1 -2α2 + 2α3 = -3 Решаем полученную систему уравнений методом Крамера. 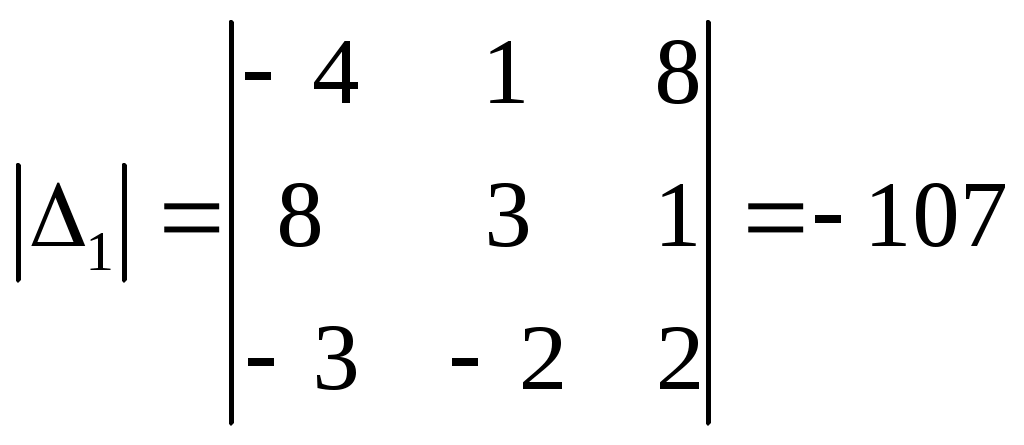 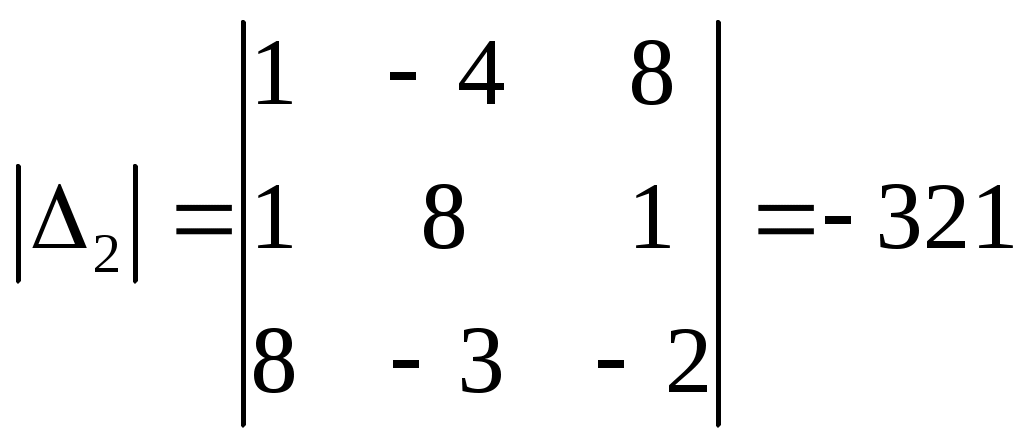 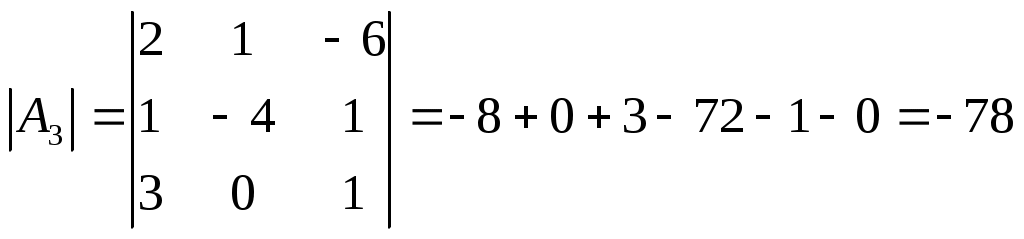 Ответ:
X = а1 + 3а2 -а3 Задание 4. Определить ранг заданной матрицы.  Решение Приведем матрицу к треугольному виду. Будем работать только со строками, так как умножение строки матрицы на число, отличное от нуля, и прибавление к другой строке для системы означает умножение уравнения на это же число и сложение с другим уравнением, что не меняет решения системы. Умножим 1ю строку на (-3). Умножим 2ю строку на (7). Добавим 2ю строку к 1й:
Умножим 2ю строку на (-10). Умножим 3ю строку на (3). Добавим 3ю строку к 2й:
Добавим 2-ую строку к 1-ой:
Ранг матрицы равен количеству ненулевых строк после приведения матрицы к ступенчатому виду, следовательно rang(A) = 2. Задание 5. Привести систему к системе с базисом методом Жордана-Гаусса и найти одно базисное решение.  Решение Запишем систему в виде:
Последовательно будем выбирать разрешающий элемент РЭ, который лежит на главной диагонали матрицы. Разрешающий элемент равен (3). На месте разрешающего элемента получаем 1, а в самом столбце записываем нули. Все остальные элементы матрицы, включая элементы столбца B, определяются по правилу прямоугольника. Для этого выбираем четыре числа, которые расположены в вершинах прямоугольника и всегда включают разрешающий элемент РЭ. НЭ = СЭ – (А*В)/РЭ РЭ - разрешающий элемент (3), А и В – элементы матрицы, образующие прямоугольник с элементами СТЭ и РЭ. Представим расчет каждого элемента в виде таблицы:
Разрешающий элемент равен (-2.33). На месте разрешающего элемента получаем 1, а в самом столбце записываем нули. Все остальные элементы матрицы, включая элементы столбца B, определяются по правилу прямоугольника. Результаты расчета элементов в виде таблицы:
Общее решение исходной системы можно записать так: x1 = 2,71 - 0,71x3 - 3,57x4 - x5 x2 = -0,43 + 0,43x3 - 2,86x4 - x5 Свободные переменные (x3 ; x4 ; x5). Примем x3 = 0; x4 = 0; x5 = 0. Тогда x1 = 2,71, x2 = -0,43. Базисное решение Х = (2,71, -0,43, 0, 0, 0). Задание 6. Найти два опорных решения канонической системы уравнений. 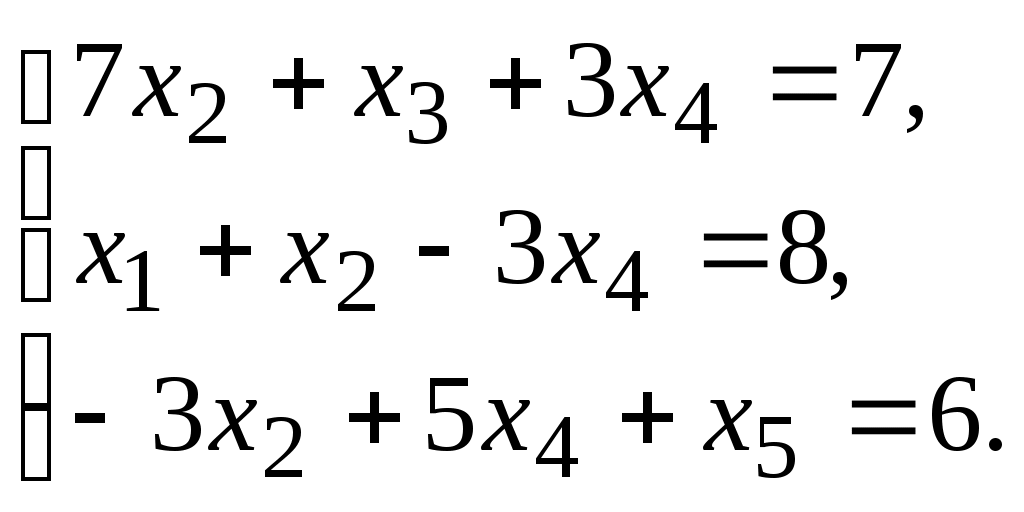 Решение
Данная система является системой с базисом относительно переменных х1, х3 и х5. Свободными неизвестными являются х2 и х4. Полагая в системе х2 = 0, и х4 = 0, получим первое опорное решение  = (8,0,7,0,6). Так как при свободных неизвестных х2 и х4 имеются положительные коэффициенты, то возможен переход к эквивалентной канонической системе. Переход осуществим согласно алгоритму преобразования однократного замещения. В качестве разрешающего столбца возьмем столбец свободной неизвестной х2. Разрешающей строкой будет первая строка. Тогда разрешающим элементом будет элемент а21 = 7.  Второе опорное решение: = (7, 4/7, 0, 0, 9).Задание 7. Найти собственные значения и собственные векторы данной матрицы.  Решение Составляем систему для определения координат собственных векторов: (6 - λ)x1 + 2x2 + 0x3 = 0 3x1 + (1 - λ)x2 + 0x3 = 0 0x1 + 0x2 + (4 - λ)x3 = 0 Составляем характеристическое уравнение и решаем его.
Для этого находим определитель матрицы и приравниваем полученное выражение к нулю. (6 - λ) • ((1 - λ) • (4 - λ)-0 • 0)-3 • (2 • (4 - λ)-0 • 0)+0 • (2 • 0-(1 - λ) • 0) = 0 После преобразований, получаем: λ(‒λ2+11*λ‒28) = 0 Корни уравнения: λ1 = 0, λ2 = 4, λ3 = 7. Подставляя последовательно полученные собственные значения в исходную систему, получим следующие три системы уравнений для нахождения соответствующих собственных векторов: 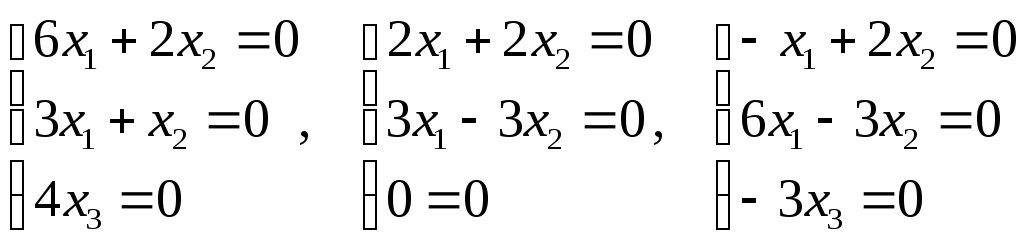 Множество собственных векторов, отвечающих собственному числу λ1 = 0, имеет вид:  .Для λ2 = 4, имеет вид:  .Для λ3 = 7, имеет вид:  .Здесь с – любое действительное число, не равное нулю. Задание 8. Даны вершины треугольника АВС. Найти уравнения его сторон и точку пересечения высот.  Решение 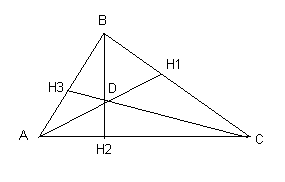 Найдем уравнения сторон треугольника: АВ:  АВ: у = 8 ‒ х. АС:  АС:  .ВС:  ВС:  Составим уравнения высот треугольника: AH1: A(0, 8), так как  , то угловой коэффициент перпендикулярной прямой  y = -  x + b8 = ∙0 + b b = 8AH1: y = - x + 8.CH3: C(14, 5), у = 8 ‒ х так как k = -1, то угловой коэффициент перпендикулярной прямой k = 1 y = x + b 5 = 14 + b b = -9. CH3: y = x – 9 Найдем точку D – точку пересечения высот.  Решив систему уравнений, получим -  .Задание 9. Привести уравнение кривой второго порядка к каноническому виду и построить линию.  Решение Выделим полные квадраты:   Разделим все выражение на -7  Это уравнение определяет гиперболу с центром в точке: C(2; 1) и полуосями: Найдем координаты ее фокусов: F1(-c;0) и F2(c;0), где c - половина расстояния между фокусами. Определим параметр c: c2 = a2 + b2 = 7 + 7/2 = 21/2 .  Тогда эксцентриситет будет равен:  Асимптотами гиперболы будут прямые:  и  Директрисами гиперболы будут прямые: Данное уравнение является каноническим уравнением гиперболы с центром в точке С(2, -1) и полуосями a = 2, b = 5. Построим гиперболу. 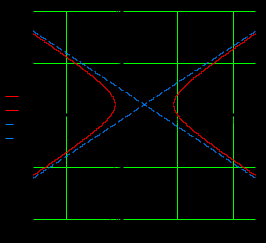 Задание 10. Построить график заданной кривой.  Решение Преобразуем уравнение к виду:  Таким образом, данное уравнение определяет параболу с вершиной в точке (1, 5) и осью симметрии х = 1. Так как а = ‒1, то ветви параболы направлены вниз. |
матрицы
элемента 
матрицы n-го порядка называется определитель матрицы (n-1)-го порядка, полученный из матрицы А вычеркиванием i-й строки и j-го столбца. 
.
.
к каноническому виду и указать геометрический тип кривой.
.