ТАУ Краткий курс лекций. Курс лекций для студентов инженернотехнических специальностей заочного отделения
 Скачать 0.69 Mb. Скачать 0.69 Mb.
|
4.4. Критерии НайквистаКритерий был сформулирован в 1932 г. американским физиком X. Найквистом, а обоснован и применен для анализа автоматических систем управления Михайловым А. В. Критерий Найквиста позволяет судить об устойчивости системы по амплитудно-фазовой характеристике разомкнутого контура системы. В этом заключается существенное преимущество критерия, так как построение амплитудно-фазовой характеристики разомкнутого контура для большинства реальных систем оказывается проще, чем построение годографа Михайлова. Особенно упрощается это построение для одноконтурных систем, состоящих из типовых звеньев. А в тех случаях, когда неизвестно математическое описание нескольких конструктивных элементов системы и оценка их свойств возможна только путем экспериментального определения частотных характеристик, критерий Найквиста является единственно пригодным. Основная формулировка критерия Найквиста: автоматическая система управления устойчива, если амплитудно-фазовая характеристика W(jw) разомкнутого контура не охватывает точку с координатами (-1; j0). Эта формулировка справедлива для систем, которые в разомкнутом состоянии устойчивы. Таковыми являются большинство реальных систем, состоящих из устойчивых элементов. На рис. 4.3, а изображены амплитудно-фазовые характеристики разомкнутого контура, соответствующие трем различным случаям: система устойчива (кривая 1); система находится на колебательной границе устойчивости (кривая 2); система неустойчива (кривая 3). Критерий Найквиста физически можно интерпретировать следующим образом. Предположим, что на входе системы (рис. 4.3, б) действует гармонический сигнал g (t) == gm Sin wt с малой амплитудой gm. Пусть частота w равна частоте wp, при которой фазовый сдвиг j(jw), создаваемый звеном W(jw), равен — p. Тогда сигнал отрицательной обратной связи окажется в фазе с сигналом g(t), и мгновенные значения сигналов будут суммироваться. 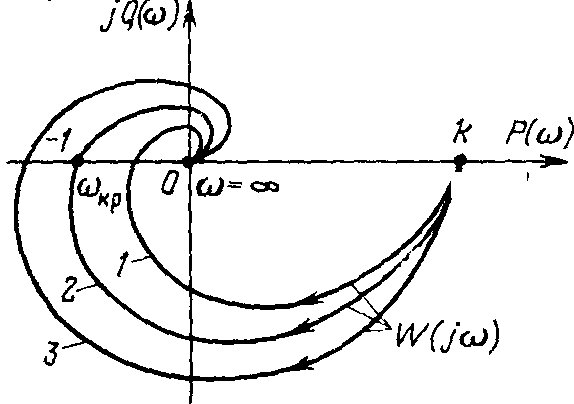 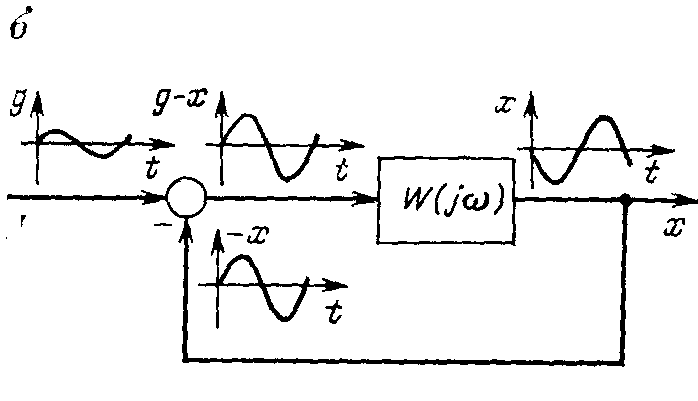 Рис. 4.3. Амплитудно-фазовые характеристики разомкнутого контура (а) и физическая трактовка (б) критерия Найквиста Если на частоте w = wp, модуль | W (jw) | = 1 (нет усиления и нет подавления), то в контуре системы будут поддерживаться незатухающие колебания даже после исчезновения внешнего воздействия g (t), т. е. система будет находиться на границе устойчивости. Характеристика W(jw) при этом проходит через точку (-1; j0). Если на частоте w = wp модуль |W(jw)| < 1 (подавление есть), то после исчезновения внешнего воздействия колебания в контуре затухнут, т. е. система устойчива, характеристика не охватывает точку (-1; j0). Если же модуль |W(jw)| > 1 (усиление есть), то амплитуда сигналов в контуре будет неограниченно возрастать, т. е. система будет неустойчивой. Характеристика W (jw) в этом случае охватит точку (-1; j0). Таким образом, особая роль точки (-1; j0) заключается в том, что она, во-первых, соответствует превращению отрицательной обратной связи в положительную, и во-вторых, является граничной между режимами усиления и ослабления сигналов звеном W (jw). Лекция 5. Типовые законы регулирования и точность сау5.1. Типовые алгоритмы регулирования САУРассмотрим типовые алгоритмы управления (законы регулирования), применяемые в линейных автоматических системах. 1. Простейший закон регулирования реализуется при помощи безынерционного звена с передаточной функцией Wp(p)=y(p)/e(p)= kп = kp. (5.1) Согласно этому выражению управляющее воздействие и в статике и в динамике пропорционально сигналу ошибки e. Поэтом такой закон регулирования называется пропорциональным (П). Преимущества П-регулятора — простота и быстродействие, недостатки — ограниченная точность (особенно при управлении объектами с большой инерционностью и запаздыванием). 2. Закон регулирования, которому соответствует передаточная функция Wp(p)= kи/p =kp/Tиp (5.2) называется интегральным (И). При интегральном законе регулирования управляющее воздействие у в каждый момент времени пропорционально интегралу от сигнала ошибки e. Поэтому И-регулятор реагирует главным образом на длительные отклонения управляемой величины от заданного значения. Кратковременные отклонения сглаживаются таким регулятором. Преимущества интегрального закона — лучшая (точность в установившихся режимах, недостатки — худшие свойства в переходных режимах (меньшее быстродействие и большая колебательность). 3. Наибольшее распространение в промышленной автоматике получил пропорционально-интегральный (ПИ) закон регулирования Wp(p)= kп + kи/p = kp + kp/Tиp = kp(Tиp + 1)/Tиp. (5.3) Благодаря наличию интегральной составляющей ПИ-закон регулирования обеспечивает высокую точность в установившихся режимах, а при определенном соотношении коэффициентов kп и kиобеспечивает хорошие показатели и в переходных режимах. 4. Наилучшее быстродействие достигается при пропорционально-дифференциальном (ПД) законе регулирования Wp(p)= kп + kдp = kp + kpTдp. (5.4) ПД-регулятор реагирует не только на величину сигнала ошибки, но и на скорость его изменения. Благодаря этому при управлении достигается эффект упреждения. Недостатком пропорционально-дифференциального закона регулирования является ограниченная точность. 5. Наиболее гибким законом регулирования (в классе линейных законов) является пропорционально-интегрально-дифференциальный(ПИД) закон Wp(p)= kп + kи/p + kдp = kp(Tиp + 1 + TиTдp2)/Tиp, (5.5) который сочетает в себе преимущества более простых законов. Коэффициенты и постоянные времени, входящие в передаточные функции типовых регуляторов, называются настроечными параметрами и имеют следующие наименования: kп, kи, kд — коэффициенты пропорциональной, интегральной и дифференциальной части; kp — передаточный коэффициент регулятора; Tи— постоянная времени интегрирования; Tд — постоянная времени дифференцирования. Параметры, входящие в различные записи (5.1) и (5.5) ПИД-закона, связаны между собой соотношениями: kп = kp; kи = kp /Tи;kд = kpTд. (5.6) |
