ТАУ Краткий курс лекций. Курс лекций для студентов инженернотехнических специальностей заочного отделения

• Название: Курс лекций для студентов инженернотехнических специальностей заочного отделения
• Анкор: ТАУ Краткий курс лекций.doc
• Дата: 15.12.2017
• Размер: 0.69 Mb.
• Имя файла: ТАУ Краткий курс лекций.doc
• Тип: Курс лекций; #11525
• страница: 7 из 9

4.2. Алгебраические критерии устойчивости

Простейшим критерием устойчивости является условие положи­тельности коэффициентов характеристического уравнения. Поло­жительность коэффициентов уравнения (8.4) является необходимым (но не достаточным!) условием устойчивости системы. Это означает, что если все коэффициенты положительны, то система может быть устойчивой или неустойчивой. Но если хотя бы один коэффициент уравнения отрицателен или равен нулю, то система неустойчива.

Наиболее распространены в инженерной практике критерии Гурвица и Рауса.

Критерий Гурвица был сформулирован и доказан в 1895 г. не­мецким математиком А. Гурвицем, который разработал свой кри­терий, решая чисто математическую задачу — задачу исследова­ния устойчивости решений линейного дифференциального уравне­ния. Применительно к задачам теории управления критерий Гур­вица можно сформулировать так:

автоматическая система, описываемая характеристическим урав­нением 8.5 устойчива, если при а₀> 0 положительны все определители D_iвида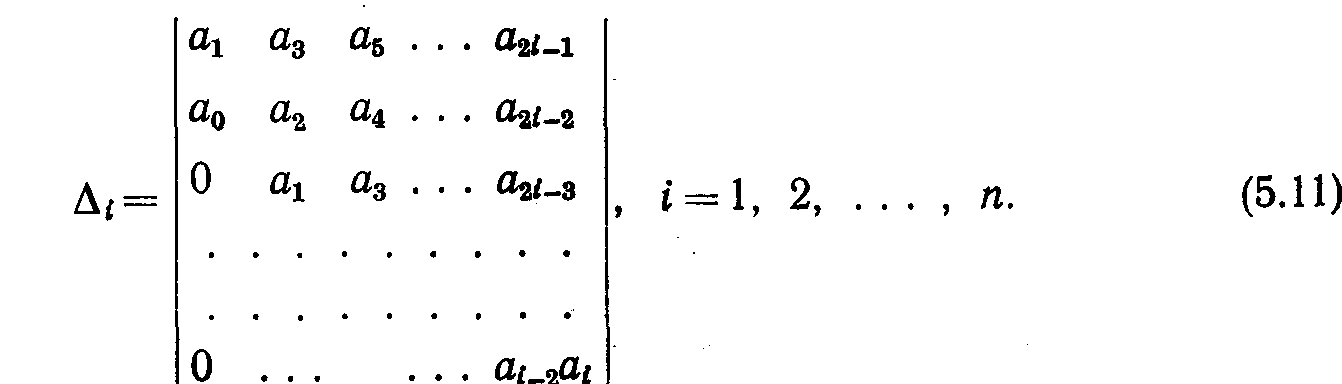


(4.9)


(Как составляется определитель матрицы i*i).

Если хотя бы один из определителей (4.9), называемых опреде­лителями Гурвица, отрицателен, то система неустойчива.

Так как последний столбец главного определителя D_n содер­жит всегда только один элемент a _n, отличный от нуля, то согласно известному свойству определителей D_n = a _n D_n-1.

Если главный определитель D_n == 0, а все остальные определи­тели положительны, то система находится на границе устойчивости. С учетом выражения (4.12) это условие распадается на два:a _n = 0 и D_n-1 = 0.

Условию а _n. = 0 соответствует один нулевой корень, т. е. апе­риодическая граница устойчивости, а условию D_n-1 = 0 - парамнимых корней, т. е. колебательная граница устойчивости.

Критерий Гурвица целесообразно применять для анализа устой­чивости систем не выше пятого порядка. При п > 5 вычисление определителей становится громоздким.

Критерий Рауса, предложенный в 1877 г. английским матема­тиком Э. Дж. Раусом, целесообразно использовать при анализе устойчивости систем выше четвертого порядка. Для этого из ко­эффициентов характеристического уравнения (4.5) составляют таблицу (табл. 4.1), в первой строке (i = 1) которой записаны ко­эффициенты уравнения с четными индексами, во второй (i =2) — с нечетными индексами, в последующих строках (i > 3) помещены коэффициенты Рауса, полученные как комбинации коэффициентов двух вышестоящих строк по формуле

r _ik = r _{i -2, k + 1} – (r _{i - 2, 1} r _{i -1, k + 1} / r _{i -1, 1}), (4.10)

где i — номер строки, k — номер столбца. Сам критерий формулируется так: автоматическая система устойчива, если. положительны все коэффициенты первого столбца таблицы Рауса (включая а₀ и а₁ ).

Таблица 4.1 Коэффициенты Рауса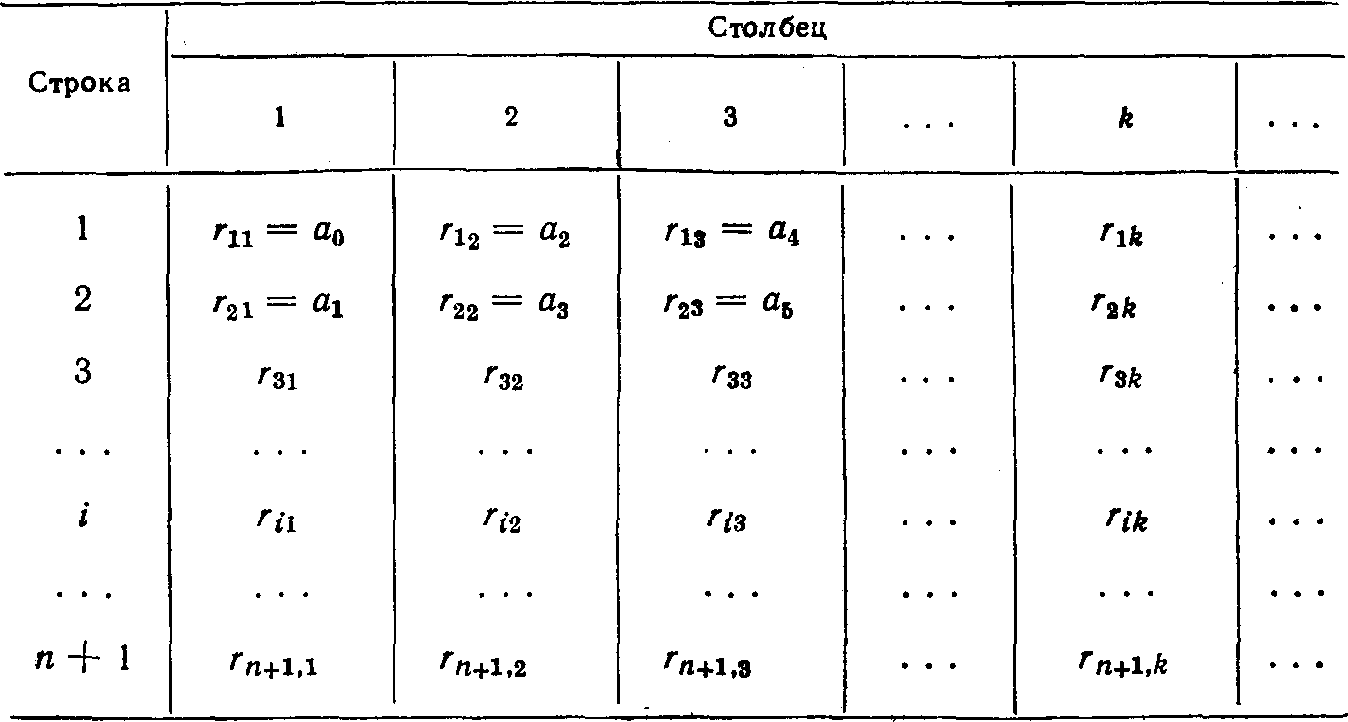



Если не все коэффициенты столбца положительны, то система неустойчива. При этом число перемен знака среди этих коэффици­ентов соответствует числу правых корней характеристического уравнения. Алгоритм вычисления коэффициентов (4.10) легко запрограмми­ровать, поэтому критерий Рауса используют для анализа систем высокого порядка (n > 5) с помощью ЭВМ.

Преимуществом критериев Гурвица и Рауса является то, что с их помощью можно оценивать устойчивость как замкнутых, так и разомкнутых систем. Вывод об устойчивости при применении этих критериев делается применительно к той системе (замкнутой или разомкнутой), уравнение которой анализируется.

Недостатком является малая наглядность.

8.3. Критерии Михайлова

Критерий Михайлова относится к группе частотных критериев устойчивости. Он был сформулирован и обоснован в 1936 г. совет­ским ученым А. В. Михайловым в работе «Гармонический метод в теории регулирования», которая получила высокую оценку и по­служила началом широкого применения частотных методов в тео­рии автоматического управления.

Критерий Михайлова так же, как критерии Гурвица и Рауса, основан на анализе характеристического уравнения системы, поэ­тому с его помощью можно судить об устойчивости замкнутых и разомкнутых систем.

Пусть левая часть характеристического уравнения, называе­мая характеристическим полиномом, имеет вид

F(p) = a₀ pⁿ+ a_n-1 p^n-1+…+ a _n-1 p+ a_n. (4.11)

Подставим в этот полином вместо переменного р чисто мнимый корень, который в дальнейшем будем обозначать jw. Тогда получим функцию комплексного переменного

F(jw) = a₀ (jw)ⁿ+ a_n-1 (jw)^n-1+…+ a _n-1 jw+ a_n, (4.12)

которую можно так же, как амплитудно-фазовую характеристику, представить в виде суммы действительной и мнимой частей:

F(jw) = P(w) + jQ(w). (4.13)

Действительная часть P(w) содержит только четные степени переменного w:

P(w) = a_n -a _{n - 2}w² + a _{n - 4}w⁴ - . . . , (4.14)

а мнимая часть Q(w)— только нечетные:

Q(w) = a_n-1w -a _{n - 3}w³ + a _{n - 5}w⁵ - . . . . (4.15)

Каждому фиксированному значению переменного w соответст­вует комплексное число, которое можно изобразить в виде вектора на комплексной плоскости. Если теперь изменять параметр w от 0 до ¥, то конец вектора F(jw) опишет некоторую линию (рис. 4.2, a), которая называется характеристической кривой или годографом Михайлова. По виду этой кривой можно судить об устойчивости системы.

Формулировка критерия Михайлова:

автоматическая система управления, описываемая уравнением п-го порядка, устойчива, если при изменении w от 0 до ¥ характеристический вектор системы F(jw) повернется против часовой стрелки на угол п p/2, не обращаясь при этом в нуль.

Это означает, что характеристическая кривая устойчивой си­стемы должна при изменении w от 0 до ¥ пройти последовательно через п квадрантов. Из выражений (4.14) и (4.15) следует, что кри­вая F (jw) всегда начинается в точке на действительной оси, уда­ленной от начала координат на величину а_n.

Характеристические кривые, соответствующие устойчивым си­стемам (рис. 4.2, б), имеют плавную спиралеобразную форму и ухо­дят в бесконечность в том квадранте, номер которого равен порядку уравнения. Если характеристическая кривая проходит п квадран­тов не последовательно или проходит меньшее число квадрантов, то система неустойчива (рис. 4.2, в).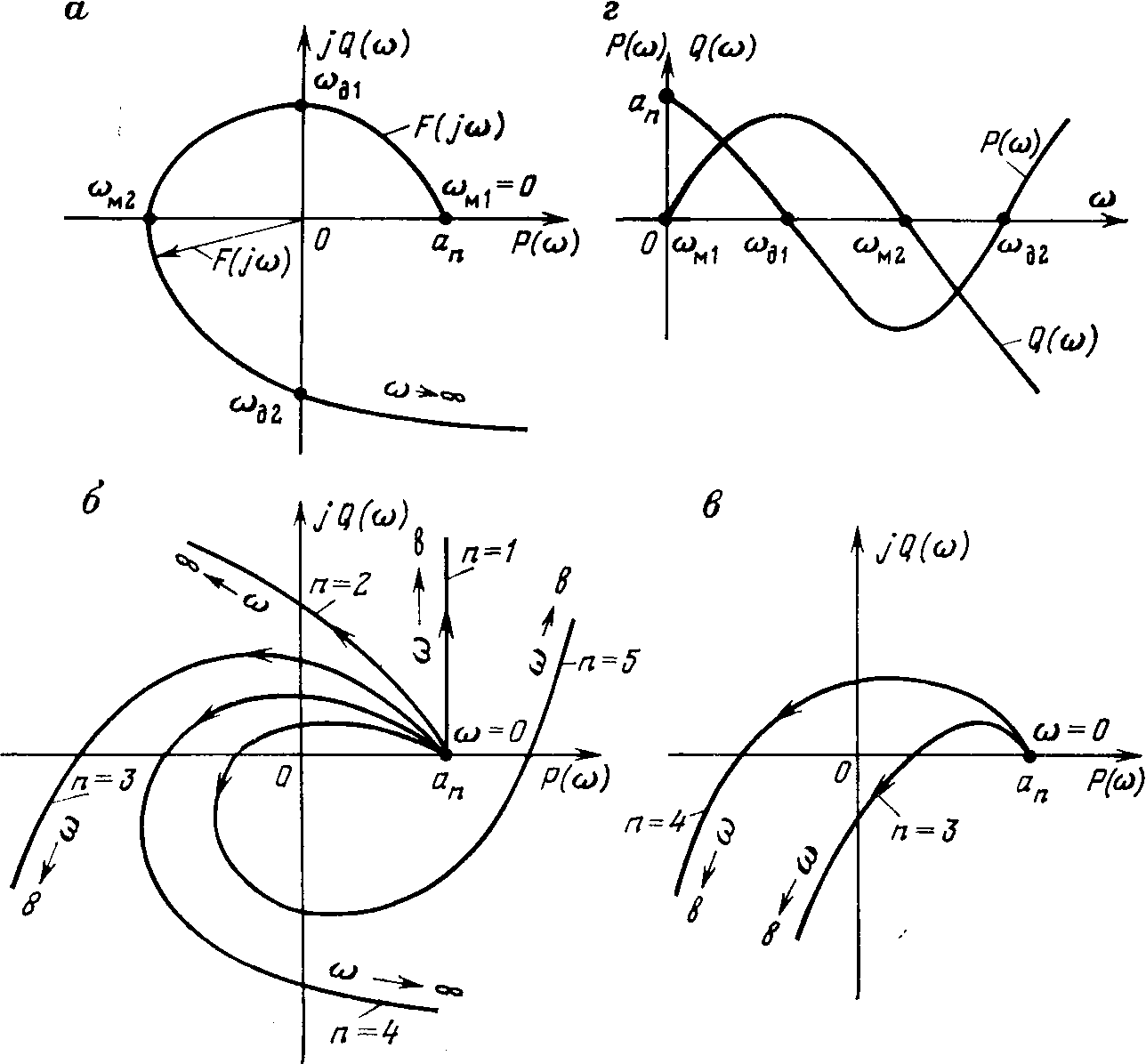


Рис. 4.2. Характеристические кривые (годографы) Михайлова
Если кривая F(jw) проходит через начало координат, то си­стема находится на границе устойчивости. Действительно, если характеристическое уравнение имеет один нулевой корень p_k = 0 (апериодическая граница устойчивости) или одну пару чисто мнимых корней p_k = ± jb_k (колебательная граница устойчивости), то функция F(jw) при w = 0 или w = b_k обратится в нуль.

В практических расчетах удобно применять следствие из критерия Михайлова: система устойчива, если действительная и мнимая части ха­рактеристической функции F(jw) обращаются в нуль пооче­редно (рис. 8.2, г), т. е. если корни уравнений P(w) = 0 и Q(w) = 0 перемежаются.

Это утверждение вытекает непосредственно из формулировки критерия Михайлова — из условия последовательного прохожде­ния кривой F(jw) через п квадрантов.

Критерий Михайлова удобно применять для анализа устойчи­вости систем высокого порядка (п > 5).