ТАУ Краткий курс лекций. Курс лекций для студентов инженернотехнических специальностей заочного отделения

• Название: Курс лекций для студентов инженернотехнических специальностей заочного отделения
• Анкор: ТАУ Краткий курс лекций.doc
• Дата: 15.12.2017
• Размер: 0.69 Mb.
• Имя файла: ТАУ Краткий курс лекций.doc
• Тип: Курс лекций; #11525
• страница: 9 из 9

5.2. Виды точностей работы САУ

7.2.1. Статическая точность.

В статическом режиме ошибки возни­кают только в статической системе, а в астатической системе они равны нулю, поэтому статическую точность оценивают только при анализе статических систем.

Статической системой управления называется система, объект и регулятор которой являются статическими элементами, т. е.

W_о(0) = k_о и W_p(0) = k_p. (5.7)

Подставляя в уравнения динамики регулируемой величины (4.15) и для ошибки (4.24) одноконтур­ной системы р == 0 и полагая для простоты x_п = 0 и x_в = 0,получим уравнения статики статической системы:

для управляемой величины

x = x_з k_pk_о( 1 + k_pk_о) +y_в k_о( 1 + k_pk_о); (5.8)

для сигнала ошибки

e = x_з ( 1 + k_pk_о)^-1 -y_в k_о( 1 + k_pk_о) ^-1. (5.9)

Первое слагаемое в правой части уравнения (4.32) характери­зует статическую ошибку по задающему воздействию, второе — статическую ошибку по возмущению. Обе эти ошибки тем больше, чем больше внешние воздействия, и тем меньше, чем больше знаме­натель ( 1 + k_pk_о). Следовательно, точность статической системы тем лучше, чем больше переда­точный коэффициент разомкнутого контура.

Точность статической системы принято оценивать коэффициен­том статизма

S == Dх_з/Dх_р, (5.10)

где Dх_р — отклонение управляемой величины х от заданного зна­чения, создаваемое возмущением у_в = у_в0 при разомкнутом кон­туре регулирования; Dх_з — отклонение управляемой величины, создаваемое тем же возмущением у_в0 в замкнутой системе. Коэффи­циент статизма показывает, во сколько раз отклонение выходной величины управляемого объекта меньше отклонения этой величины неуправляемого объекта (при одном и том же значении возмущаю­щего воздействия). Очевидно, что Dх_р=Dy_в0k_o и Dх_з = Dy_в0k_o/( 1 + k_pk_о). Отсюда коэффициент статизма

S == ( 1 + k_pk_о)^-1== ( 1 + k)^-1, (5.11)

где k = k_pk_о— передаточный коэффициент разомкнутого контура.

Точность статической системы считается удовлетворительной, если коэффициент S = 0,1 —0,01. Следовательно, общий переда­точный коэффициент разомкнутого контура статической системы должен находиться в диапазоне 10 —100

5.3. Понятие и показатели качества управления

Качество автоматической системы управления определяется совокупностью свойств, обеспечиваю­щих эффективное функционирование как самого объекта управле­ния, так и управляющего устройства, т. е. всей системы управле­ния в целом. В теории автоматического управления термины «качество управления» исполь­зуют в узком смысле: рассматривают только статические и динамические свойства системы. Такие свойства системы, выраженные в количественной форме, называют показателями качества управления. Эти свойства предо­пределяют точность поддержания управляемой величины на заданном уровне в установившихся и пе­реходных режимах, т. е. обеспечивают эффективность процесса управления.

В частности, нами была рассмотрена точность системы в установившихся режимах. Теперь мы будут рассматривать показатели качества, характеризующие точность системы в переходных режимах.

Точность системы в переходных режимах оценивают при помощи прямых и косвенных показателей. Прямые показатели определяют по графику переходного процесса, возникающего в системе при ступенчатом внешнем воздействии. Косвенные показатели качества определяют по распределению корней характеристического урав­нения или по частотным характеристикам системы.

К особой категории показателей качества относятся так назы­ваемые интегральные оценки, которые вычисляют либо непосредст­венно по переходной функции системы, либо по коэффициентам передаточной функции системы.

Вспомним, по лекции точность системы в переходных режимах определяется величи­нами отклонений управляемой переменной х(t) от заданного зна­чения х_з(t) и длительностью существования этих отклонений. Ве­личина и длительность отклонений зависят от характера переход­ного процесса в системе. Характер переходного процесса в свою очередь зависит как от свойств системы, так и от места приложения внешнего воздействия.

При самой общей оценке качества обращают внимание прежде всего на форму переходного процесса. Различают следующие типовые переходные процессы (рис. 5.1): колебатель­ный (кривая 1), монотонный (кривая 2) и апериодический (кривая 3).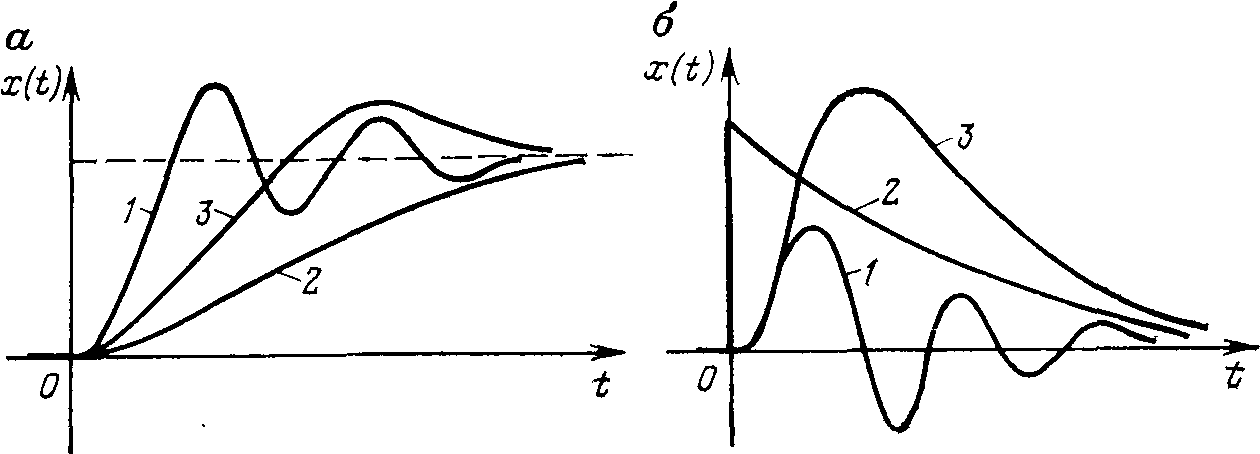



Рис. 5.1. Типовые переходные процессы:

а — по заданию; б—по возмущению
Каждый из трех типовых процессов имеет свои преимущества и недостатки, и предпочтение той или иной форме процесса делают с учетом особенностей управляемого объекта. Так, например, в электромеханических объектах со сложными кинематическими пе­редачами (лифты, экскаваторы, подъемные установки) нежелательны рез­кие знакопеременные усилия, и поэтому при выборе настроек си­стем управления такими объектами стремятся к апериодическим и монотонным процессам. В рассмотренной нами системе управления обогатительным аппаратом допустимы колебательные переход­ные процессы, так как кратковременные отклонения управляемых величин не ухудшают существенно показатели обогащения.

10.2. Прямые показатели.

Рассмотрим основные показатели качества управления приме­нительно к типовой одноконтурной системе регулирования .

На графиках переходных процессов, вызванных ступенчатым изменением задающего воздействия х_з(t) (рис. 5.2, а) и возмущения у_в, действующего на входе объекта (рис. 5.2, б), за начало отсчета для выходной величины х(t) принято значение х(- 0), которое было до подачи ступенчатого воздействия.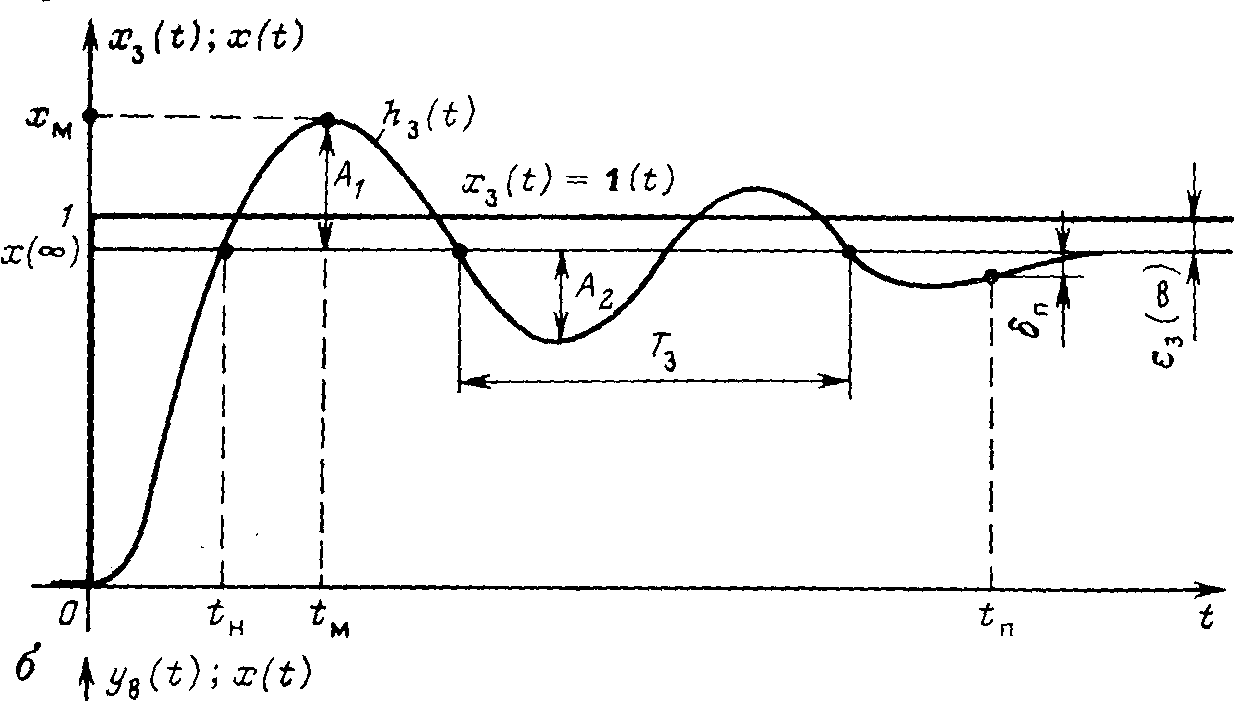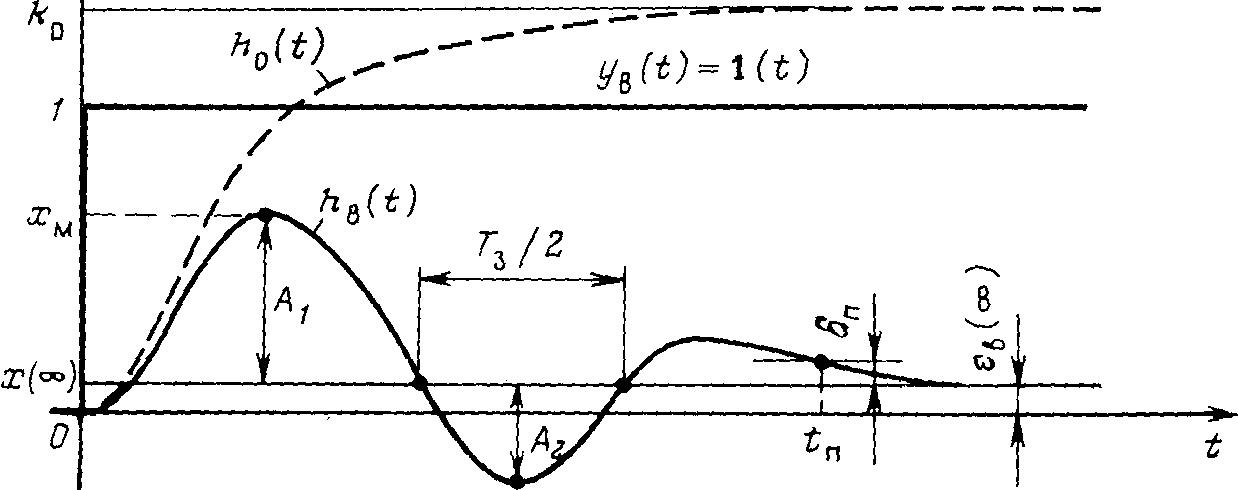



Рис. 5.2. Прямые показатели качества процесса регулирования:

а—по каналу задания; б—по каналу возмущения
Одним из главных прямых показателей качества является перерегулирование s (%), которое равно отношению первого макси­мального отклонения управляемой переменной х(t) от ее устано­вившегося значения х(¥) к этому установившемуся значению (см. рис. 5.2, а):

s = 100 (х_м - х(¥)) / х(¥) = 100 A₁ / х(¥). (5.1)

Качество управления считается удовлетворительным, если пе­ререгулирование не превышает 30—40 %.

Для переходных процессов, вызванных возмущающим воздейст­вием у_в на входе объекта (см. рис. 5.2, б), перерегулирование можно определять как отношение второго (отрицательного) макси­мального отклонения А₂ к первому максимальному отклонению A₁:

s = 100 А₂ / (х_м - х(¥)) = 100 А₂ / A₁. (5.2)

Показатель, вычисляемый по данной формуле для переходных процессов по каналу возмущения, называют также колебатель­ностью.

Другой важной характеристикой таких процессов служит динамический коэффициент регулирования R_д(%), который равен отношению первого максимального отклонения х_м к отклонению выходной переменной х(t) нерегулируемого объекта, вызванному тем же возмущением, т.е.

R_д = 100 х_м / k_o . (5.3)

Коэффициент R_дпоказывает, насколько эффективно компенси­рующее действие регулятора на объект.

Отметим, что и само первое максимальное отклонение х_м, воз­никающее от возмущения на входе объекта, является показателем качества. При формировании требований к системе указывают до­пустимое значение максимального отклонения.

Длительность существования динамических отклонений управ­ляемой величины х (t) от ее нового установившегося значения х (¥) принято оценивать с помощью нескольких характерных моментов времени. Самым важным из этой группы показателей является длительность переходного процесса (время регулирования) t_п — интервал времени от момента приложения ступенчатого воздейст­вия до момента, после которого отклонения управляемой величины х(t) от ее нового установившегося значения х (¥) становятся меньше некоторого заданного числа d_п, т. е. до момента, после ко­торого выполняется условие | х(t) — х (¥) | < d_п . В промышленной автоматике величину d_п принимают обычно равной 5 % от установившегося значения х (¥) [d_п == 0,05 х (¥) ]. При оценке длительности переходных процессов, вызванных еди­ничным возмущающим воздействием у_в на входе объекта (см. рис. 5.2, б), величину d_п можн принимать равной 5 % от значения передаточного коэффициента объекта k_o [d_п==0,05k_o,


Библиографический список
1. Теория автоматического управления. Часть 1 / Под ред. Воронова А.А. – М.: Высшая школа, 1986.-367 с.

2. Петровский В.С., Харитонов В.В. Автоматика и автоматизация производственных процессов лесопромышленных предприятий. – М,: Лесная промышленность, 1990. – 240 с.

3. Пиргач Н.С. Пиргач В.С. Автоматическое регулирование и регуляторы. - М,: Лесная промышленность, 1975. -264 с.

4. Ползик П.В. и др. Автоматика и автоматизация производственных процессов деревообрабатывающих предприятий. – М,: Лесная промышленность, 1987. – 440 с.

5. Теория автоматического управления / Под ред. Соломенцева Ю.М. . – М,: Машиностроение, 1992. -268 с.

6. Савельев А.Д. Прикладная теория цифровых автоматов. – М,: Высшая школа, 1987. -272 с.

7. Ерофеев А.А. Автоматизированные системы управления строительными машинами. – Л,: Машиностроение, 1977.-224 с.

8. Воронов А.А., Титов В.К., Новогранов Б.И. Основы теории автоматического регулирования и управления. – М,: Высшая школа, 1977. – 517 с.

9. Боронихин А.С., Гризак Ю.С. Основы автоматизации производства. – М,: Стройиздат, 1981. – 343 с.

10. Зайцев Г.Ф. Теория автоматического управления и регулирования.-Киев,:Высшая школа,1988.-431с.

11. Теория автоматического управления./ Под ред.Шаталова А.С..-М,:Высшая школа,1978.- 445с.