загрузка. загружено. Курс лекций для студентов специальности 071900 (230201) Информационные системы и технологии
 Скачать 0.78 Mb. Скачать 0.78 Mb.
|
Лекция 8. Нечеткие знания. Основы теории нечетких множеств.При попытке формализовать человеческие знания исследователи вскоре столкнулись с проблемой, затруднявшей использование традиционного математического аппарата для их описания. Существует целый класс описаний, оперирующих качественными характеристиками объектов (много, мало, сильный, очень сильный и т. п.). Эти характеристики обычно размыты и не могут быть однозначно интерпретированы, однако содержат важную информацию (например, «Одним из возможных признаков гриппа является высокая температура»). Кроме того, в задачах, решаемых интеллектуальными системами, часто приходится пользоваться неточными знаниями, которые не могут быть интерпретированы как полностью истинные или ложные (логические true/false или 0/1). Существуют знания, достоверность которых выражается некоторой промежуточной цифрой, например 0.7. Как, не разрушая свойства размытости и неточности, представлять подобные знания формально? Для разрешения таких проблем в начале 70-х американский математик Лотфи Заде предложил формальный аппарат нечеткой (fuzzy) алгебры и нечеткой логики [Заде, 1972]. Позднее это направление получило широкое распространение [Орловский, 1981; Аверкин и др., 1986; Яшин, 1990] и положило начало одной из ветвей ИИ под названием — мягкие вычисления (soft computing). Л. Заде ввел одно из главных понятий в нечеткой логике — понятие лингвистической переменной. Лингвистическая переменная (ЛП) — это переменная, значение которой определяется набором вербальных (то есть словесных) характеристик некоторого свойства. Например, ЛП «рост» определяется через набор {карликовый, низкий, средний, высокий, очень высокий}. Основы теории нечетких множествЗначения лингвистической переменной (ЛП) определяются через так называете нечеткие множества (НМ), которые в свою очередь определены на некотором базовом наборе значений или базовой числовой шкале, имеющей размерность. Каждое значение ЛП определяется как нечеткое множество (например, НМ «низкий рост»). Нечеткое множество определяется через некоторую базовую шкалу В и функцию принадлежности НМ — Таким образом, нечеткое множество В — это совокупность пар вида (х, где х: — i-е значение базовой шкалы. Функция принадлежности определяет субъективную степень уверенности эксперта в том, что данное конкретное значение базовой шкалы соответствует определяемому НМ. Эту функцию не стоит путать с вероятностью, носящей объективный характер и подчиняющейся другим математическим зависимостям. Например, для двух экспертов определение НМ «высокая» для ЛП «цена автомобиля» в условных единицах может существенно отличаться в зависимости от их социального и финансового положения. «Высокая_цена_автомобиля_1» = {50000/1 + 25000/0.8 + 10000/0.6 + 5000/0.4}. «Высокая_цена_автомобиля_2» = {25000/1 + 10000/0.8 + 5000/0.7 + 3000/0.4} Пример 1.6 Пусть перед нами стоит задача интерпретации значений ЛП «возраст», таких как «молодой» возраст, «преклонный» возраст или «переходный» возраст. Определим «возраст» как ЛП (рис. 1.6). Тогда «молодой», «преклонный», «переходный» будут значениями этой лингвистической переменной. Более полно, базовый набор значений ЛП «возраст» следующий: В - {младенческий, детский, юный, молодой, зрелый, преклонный, старческий}. Д 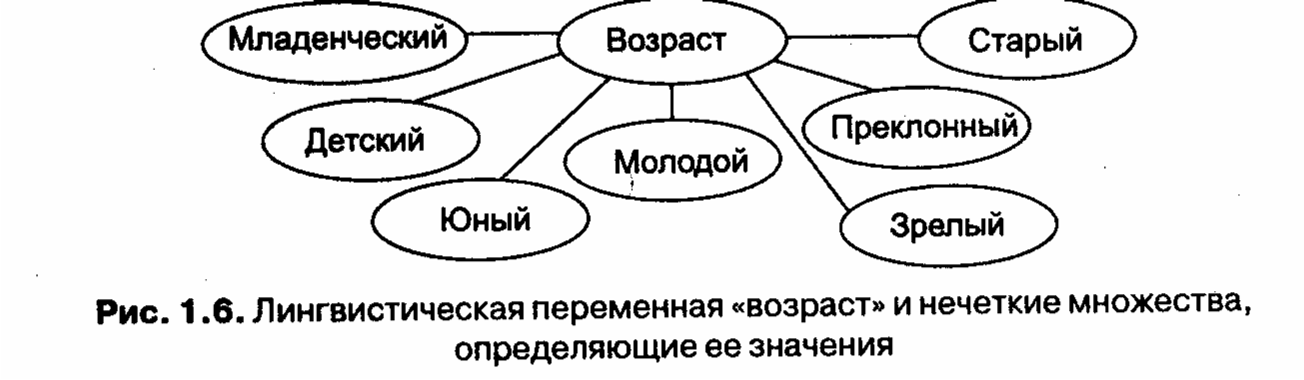 ля ЛП «возраст» базовая шкала — это числовая шкала от 0 до 120, обозначающая количество прожитых лет, а функция принадлежности определяет, насколько мы уверены в том, что данное количество лет можно отнести к данной категории возраста. На рис. 1.7 отражено, как одни и те же значения базовой шкалы могут участвовать в определении различных НМ. Например, определить значение НМ «младенческий возраст» можно так: «младенческий»= Рисунок 1.8 иллюстрирует оценку НМ неким усредненным экспертом, который ребенка до полугода с высокой степенью уверенности относит к младенцам (т = 1). Дети до четырех лет причисляются к младенцам тоже, но с меньшей степенью уверенности (0.5< m <0.9), а в десять лет ребенка называют так только в очень редких случаях — к примеру, для девяностолетней бабушки и 15 лет может считаться младенчеством. Таким образом, нечеткие множества позволяют при определении понятия учитывать субъективные мнения отдельных индивидуумов. Лекция 9. Нечеткие знания. Операции с нечеткими знаниямиДля операций с нечеткими знаниями, выраженными при помощи лингвистических переменных, существует много различных способов. Эти способы являются в основном эвристиками. К примеру, операция «ИЛИ» часто задается так [Аверкин и др., 1986; Яшин, 1990]: (так называемая логика Заде) или так: (вероятностный подход). Усиление или ослабление лингвистических понятий достигается введением специальных квантификаторов. Например, если понятие «старческий возраст» определяется как {60/0,6+70/0,8+80/0,9+90/1}, то понятие «очень старческий возраст» определится как то есть «очень старческий возраст» равен {60/0,36+70/0,64+80/0,81+90/1} Для вывода на нечетких множествах используются специальные отношения и операции над ними (подробнее см. работу [Орловский, 1981]). Одним из первых применений теории НМ стало использование коэффициентов уверенности для вывода рекомендаций медицинской системы MYCIN [Shortliffe, 1976]. Этот метод использует несколько эвристических приемов. Он стал примером обработки нечетких знаний, повлиявших на последующие системы. В настоящее время в большинство инструментальных средств разработки систем, основанных на знаниях, включены элементы работы с НМ, кроме того, разработаны специальные программные средства реализации так называемого нечеткого вывода, например «оболочка» FuzzyCLIPS. Использование коэффициента уверенностиКоэффициент уверенности (разработал Шортлифф) вводится для измерения степени доверия к любому данному заключению, являющемуся результатом полученных к этому моменту сведений. Коэффициент уверенности (КУ)- это разность между двумя мерами: КУ [h:e] = МД [h:e] - МНД [h:e], В этом выражении КУ [h:e] - уверенность в гипотезе h с учетом свидетельства e; МД [h:e] - мера доверия h при заданном e; МНД [h:e] - мера недоверия h при свидетельствах e. КУ может изменяться от -1 (абсолютная ложь) до +1 (абсолютная истина), принимая так же все промежуточные значения, причем 0 означает полное незнание. Значения же МД и МНД, с другой стороны, могут изменяться лишь от 0 до 1. Таким образом, КУ - это простой способ взвешивания свидетельств “за” и “против”. Заметим, что эта формула не позволяет отличить случай противоречащих свидетельств (и МД, и МНД обе велики) от случая недостаточной информации (и МД, и МНД обе малы), что иногда было бы полезно. Заметим также, что ни КУ, ни МД, ни МНД не являются вероятностными мерами. Они просто позволяют упорядочить гипотезы в соответствии с той степенью обоснованности, которая у них есть. Взвешивание свидетельствТо, что было добавлено Шортлиффом, - это формула уточнения, по которой новую информацию модно было непосредственно сочетать со старыми результатами. Она применяется к мерам доверия (МД) и мерам недоверия (МНД), связанным с каждым предположением. Формула для МД выглядит следующим образом: МД [h:e1,e2]=МД [h:e1]+МД [h:e2](1 - МД [h:e1]), где запятая между e1 и e2 означает, что e2 следует зе e1. Аналогичным образом уточняются значения МНД. Смысл формулы состоит в том, что эффект второго свидетельства (e2) на гипотезу h при заданном свидетельстве e1 сказывается в смещении МД в сторону полной определенности на расстояние, зависящее от второго свидетельства. Эта формула имеет два важных свойства: 1. Она симметрична в том смысле, что порядок e1 и e2 не существенен. 2. По мере накопления подкрепляющих свидетельств МД (или МНД) движется к определенности. Пример: Правило 1 ЕСЛИ X держит собаку И X регулярно делает отчисления в фонд развития зоопарков ТО X любит животных. Правило 2 ЕСЛИ X является членом общества охраны животных ИЛИ X регулярно посещает зоопарк ТО X любит животных Примем, что значения МД для этого X таковы: 1а. X держит собаку 0,8} 1б. X регулярно делает отчисления в фонд развития зоопарков 0,75} И <=> min 2а. X является членом общества охраны животных 0,4} 2б. X регулярно посещает зоопарк 0,6} ИЛИ <=> max Тогда гипотеза, что X любит животных, поддерживается на уровне 0,75 правилом 1 и на уровне 0,6 правилом 2. Применяя приведенную формулу, получим МД [любит животных: правило1, правило2]= = МД [любит животных: правило1]+ + МД [любит животных: правило 2] (1-МД[любят животных: правило 1]) = 0,75+0,6+0,25=0,9 Таким образом, объединенная мера доверия оказывается выше, чем при учете каждого свидетельства, взятого отдельно. Схема Шортлиффа допускает также возможность того, что, как и данные, правила могут быть ненадежными. Это позволяет описывать более широкий класс ситуаций. Каждое правило снабжено “коэффициентом ослабления”, числом от 0 до 1, показывающим надежность этого правила. Пример: Правило 3 (надежность 0,64) ЕСЛИ X посещает занятия И X готовит домашнее задание ТО X учится на отлично. Правило 4 (надежность 0,8) ЕСЛИ X получает повышенную стипендию ИЛИ X получил президентскую стипендию ТО X учится на отлично. Здесь правило 4 вызывает больше доверия, чем правило 3. Если степени поддержки условий таковы: 3а. X посещает занятия 0,88} 3б. X готовит домашнее задание 0,5} И <=> min 4а. X получает повышенную стипендию 0,5} 4б. X получил президентскую стипендию 0,7} ИЛИ <=> max то немодифицированная сила заключений будет равна 0,5 и 0,7, но эти МД следует умножить на ослабляющий коэффициент 0,64 и 0,8, что дает 0,32 для правила 3 и 0,56 для правила 4. Применяя формулу уточнения Шортлиффа получаем МД [отличник : П3, П4] = 0,32+0,560,68 = 0,7008. Эмпирические результаты достаточно ободряющие, чтобы оправдывать дальнейшее их использование и изучение. Список литературыАбдикеев, Н. М. Проектирование интеллектуальных систем в экономике / Н. М. Абдикеев. М.: Экзамен, 2004. Романов, В. П. Интеллектуальные информационные системы в экономике / В. П. Романов. М.: Экзамен, 2003. Андрейчиков, А. В. Интеллектуальные информационные системы / А. В. Андрейчиков, О. Н. Андрейчикова. М.: Финансы и статистика, 2004. Усков, А. А. Интеллектуальные технологии управления. Искусственные нейронные сети и нечеткая логика / А. А. Усков, А. В. Кузьмин. М.: Горячая линия – Телеком, 2004. Корнеев, В. В. Базы данных. Интеллектуальная обработка информации / В. В. Корнеев, А. Ф. Гареев, С. В. Васютин, Р. В. Райх. М.: Нолидж, 2000. Гаврилова, Т. А. Базы знаний интеллектуальных систем / Т. А. Гаврилова, В. Ф. Хорошевский. СПб.: Питер, 2000. Заенцев, И. В. Нейронные сети: основные модели: Курс лекций / И. В. Заенцев. Ворон. гос. ун-т. Воронеж, 2001. Представление и использование знаний: Пер. с япон. / Под ред. Х. Уэно, М. Исидзука. М.: Мир, 1989. Асаи, К. Прикладные нечеткие системы: Пер с япон. / К. Асаи, Д. Ватада, С. Иваи и др. // Под ред. Т. Тэрано, К. Асаи, М. Сугэно. М.: Мир, 1993. Приобретение знаний: Пер. с япон. / Под ред. С. Осуги, Ю. Саэки. М.: Мир, 1990. Сотник, С. Л. Основы проектирования систем искусственного интеллекта: Конспект лекций / С. Л. Сотник. М.: Мир, 1998. Уотермен, Д. Руководство по экспертным системам: Пер. с англ. / Д. Уотермен. М.: Мир, 1989. Брукинг, А. Экспертные системы. Принципы работы и примеры: Пер. с англ. / А. Брукинг, П. Джонс, Ф. Кокс и др. // Под ред. Р. Форсайта. М.: Радио и связь, 1987.  Дополнительная литература Хант Э. Искусственный интеллект. М.1978. Р. Harmon. The AI Tools Market The Market for Intelligent Software Building Tools. Part I. Intelligent Softwane Strategies, 1994, v 10, n.2, pp.1-14. Р. Harmon. The market for intelligent software pnducts Intelligent Software Strategies, 1992, v.8, n.2, рр.5-12. B.R. Clements and F. Preto. Evaluating Commencial Real Time Expert System Software for Use in the Process Industries. C&I, 1993, рр. 107-114. B. Moore. Memorandum. 1993, April. Gensym Corparation. Р. Богатырев. "Этот странный придуманный мир". Компьютерра. ©30-33. 1996 год. ПРИЛОЖЕНИЯПРИЛОЖЕНИЕ А.ПЕРЕЧЕНЬ КЛЮЧЕВЫХ СЛОВ
|
