Курс лекций ТДУ АТ. Курс лекций для студентов специальности 190401 Электроснабжение железных дорог
 Скачать 1.39 Mb. Скачать 1.39 Mb.
|
1.4. Классификация логических устройствЛогические устройства могут быть классифицированы по способу ввода – вывода. При этом они бывают последовательные, параллельные и смешанные. Последовательным называется устройство, в котором входные сигналы поступают на вход, а выходные снимаются с выхода последовательно – разряд за разрядом. Параллельными называются устройства, в которых все разряды входных переменных подают на вход, и все разряды выходных переменных снимаются с выхода одновременно. В смешанных устройствах бывают один вход и несколько выходов или несколько входов и один выход. По принципу действия логические устройства различаются комбинационные и последовательностные. Комбинационные логические устройства – это автоматы без памяти, в которых выходные сигналы однозначно определяются набором входных сигналов, действующих только в настоящий момент времени, и не зависят от сигналов, действовавших ранее. Последовательностные логические устройства – это автоматы с памятью, выходные сигналы которых определяются всей последовательностью входных сигналов, действовавших за некоторое время, их также называют цифровыми автоматами. 1.5. Способы записи функций алгебры логикиР 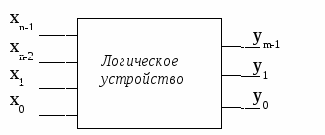 ассмотрим некоторое параллельное логическое устройство (рис. 1.3), на входе которого присутствует n-разрядный двоичный код, а на выходе m-разрядный двоичный код, причём n m. Рис. 1.3. Логическое устройство, содержащее n входов и m выходов Чтобы описать поведение логического устройства необходимо определить зависимость каждой из m выходных переменных yi от всех входных сигналов хn-1,…x1, x0. Зависимость выходных переменных y, выраженная через совокупность входных переменных (хn-1,…x1, x0), записанная с помощью операций алгебры логики, называется функцией алгебры логики (ФАЛ). Задать ФАЛ – это определить значения yi для всех возможных сочетаний входных переменных (хn-1,…x1, x0). Очевидно, что для n-разрядного входного кода существует 2n различных значений yi. ФАЛ называется полностью определённой, если заданы все 2n её значений yi. Если часть значений yi не задана, то ФАЛ называется частично определённой (недоопределённой). Для описания ФАЛ могут быть использованы различные способы, например: 1) словесная форма; 2) таблица истинности; 3) алгебраические выражения. Наиболее наглядно ФАЛ представляется таблицей истинности, пример которой для y = f(x2, x1, x0) представлен в таблице 1.4. Таблица 1.4 ФАЛ, заданная таблицей истинности для трёх входных переменных
Чтобы записать ФАЛ в виде алгебраического выражения можно использовать две стандартные формы представления: ДНФ – дизъюнктивно нормальная функция; КНФ – конъюнктивно нормальная функция. ДНФ – это логическая сумма элементарных логических произведений, в каждое из которых аргумент x или его инверсия входит один раз. ДНФ получают из таблицы истинности по следующему правилу: - для каждого набора переменных, на котором y= 1, записываются элементарные логические произведения входных переменных, причем переменная x = 0 записывается с инверсией; - логически суммируются все элементарные логические произведения. Из заданной таблицы истинности получается следующая ДНФ: КНФ – это логическое произведение элементарных логических сумм, в каждую из которых аргумент x или его инверсия входят один раз. КНФ получают из таблицы истинности по правилу: - для каждого набора переменных, на котором y = 0, записываются элементарные логические суммы входных переменных, причём переменная х = 1, записывается с инверсией; - логически перемножаются все элементарные логические суммы. Из заданной таблицы истинности получается следующая КНФ: Полученные алгебраические выражения (1.2) и (1.3) равносильны. Представление ФАЛ в виде ДНФ или КНФ выбирают с целью получить возможно более короткую запись алгебраического выражения. Для этого анализируют таблицу истинности: если у выходной переменной yбольше нулей, чем единиц, проще записать ДНФ; если больше единиц, чем нулей, проще записать КНФ. |
