Курс лекций ТДУ АТ. Курс лекций для студентов специальности 190401 Электроснабжение железных дорог
 Скачать 1.39 Mb.
|
2.5. Минимизация системы ФАЛЕсли логическое устройство имеет m выходов, то его структура описывается системой m ФАЛ. Минимизация структуры такого устройства может быть выполнена с использованием метода карт Вейча – Карно раздельно для каждого выхода. При этом может оказаться, что структура всего устройства получится неоптимальной. Достижение оптимального результата может быть реализовано выделением в каждом выражении одинаковых импликант, то есть выделением на картах одинаковых областей. Сформировав такую импликанту только один раз, можно использовать её для нескольких из m уравнений, сократив, таким образом, общее число логических элементов в технической реализации логического устройства. Рассмотрим пример минимизации системы ФАЛ из трёх функций Y1, Y2, Y3 для трёх переменных X2, X1, X0 [1], заданных таблицей истинности.
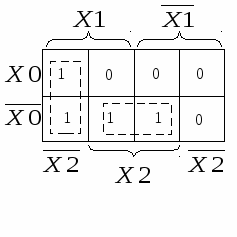
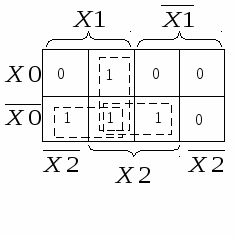
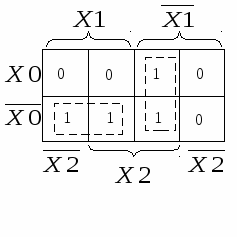
Составим карты Вейча – Карно и проведём минимизацию для получения МДНФ раздельно для каждого выхода.
Техническая реализация системы ФАЛ, уравнения которой получены раздельно для каждого выхода, потребует три инвертора, семь элементов 2И, два элемента 2ИЛИ и один элемент 3ИЛИ, то есть всего 13 элементов. Если проанализировать полученные уравнения, можно выделить в них общие члены  и  . Сформировав их только один раз, можно упростить техническую реализацию системы ФАЛ. В этом случае потребуется три инвертора, пять элементов 2И, два элемента 2ИЛИ и один элемент 3ИЛИ, то есть всего 11 элементов. Структурная схема такого логического устройства представлена на рис. 2.4.
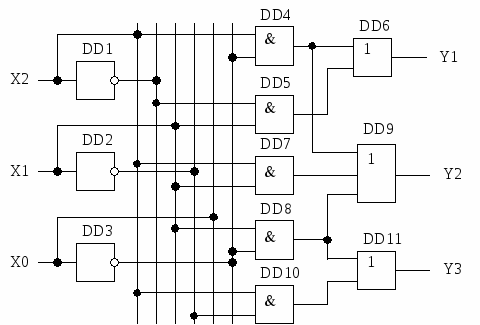
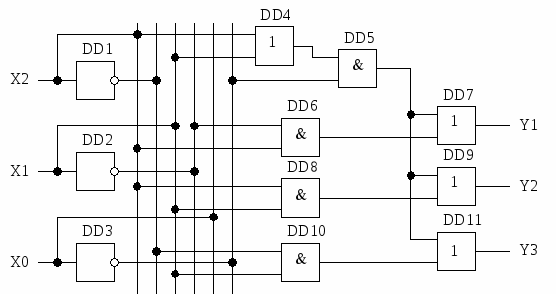
Рис. 2.4. Структурная схема ЛУ для Y1, Y2 и Y3 Нетрудно заметить, что для Y1 не использована область 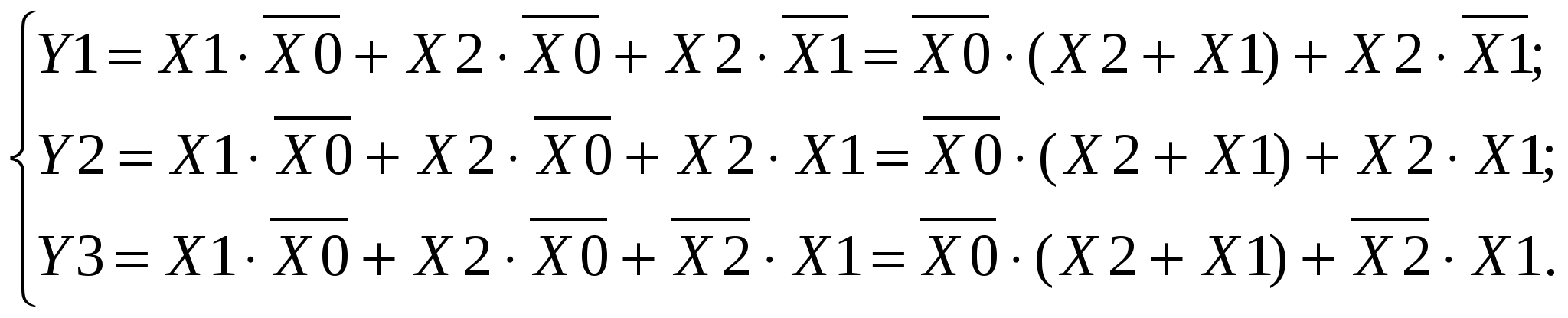 , а для Y3 область . Эти области при раздельной минимизации получаются лишними. Но если стремиться к получению наилучшего результата минимизации системы ФАЛ, можно добавить эти импликанты в соответствующие уравнения, а затем провести дополнительные преобразования по теоремам алгебры логики: (2.7)Реализация такой схемы логического устройства потребует три инвертора, четыре элемента 2И и четыре элемента 2ИЛИ, то есть тоже 11 элементов. Однако из схемы исключается элемент 3ИЛИ, что является преимуществом, так как упрощает реализацию. Структурная схема такого логического устройства представлена на рис. 2.5.
Рис. 2.5. Структурная схема ЛУ для Y1, Y2 и Y3 по выражению (2.7) Контрольные вопросы 1. В чём заключается цель минимизации логических устройств? 2. Почему реализация логического устройства по ДНФ или КНФ, полученным непосредственно из таблицы истинности, не будет оптимальной? 3. Почему преобразования по теоремам алгебры логики не всегда могут обеспечить получение минимальной технической реализации логического устройства? 4. Что такое карта Вейча – Карно? 5. Приведите примеры карт Вейча – Карно для двух, трёх и четырёх переменных. 6. Приведите алгоритм минимизации ФАЛ с помощью карт Вейча – Карно. 7. Что такое импликанта? 8. В чём заключается порядок минимизации недоопределённой ФАЛ? 9. Почему замена всех необязательных значений недоопределённой ФАЛ может привести к отрицательному результату минимизации? 10. Почему желательно проводить минимизацию и по единичным и по нулевым значениям ФАЛ? 11. Каковы особенности минимизации системы ФАЛ? 12. Почему минимизация системы ФАЛ раздельно для каждого выхода может привести к неоптимальному результату технической реализации логического устройства в целом? |
.
.
.
