Курс лекций ТДУ АТ. Курс лекций для студентов специальности 190401 Электроснабжение железных дорог
 Скачать 1.39 Mb. Скачать 1.39 Mb.
|
2. МИНИМИЗАЦИЯ функций алгебры ЛОГИКИ2.1. Цель минимизации ФАЛЛогическое устройство можно синтезировать непосредственно по алгебраическому выражению, представленному в виде ДНФ или КНФ. Однако полученная схема не будет оптимальной. Поэтому полученные из таблицы истинности ФАЛ необходимо минимизировать. Целью минимизации ФАЛ является снижение стоимости её технической реализации. Если проанализировать формулу ДНФ (1.2), то можно заметить, что в ней возможны вынесения за скобки общих сомножителей (значений переменных или их инверсий). Такие же преобразования можно провести и в формуле КНФ (1.3), если алгебраически перемножить элементарные логические суммы, а затем привести подобные члены и вынести за скобки общие сомножители. В конечном итоге можно получить выражение, содержащее гораздо меньше переменных. Например, для формулы (1.2) можно провести следующие преобразования: Воспользовавшись теоремами №4 В результате мы получили минимальную дизъюнктивно нормальную функцию МДНФ. Для её технической реализации (без учёта инверторов для получения инверсных значений входных переменных) потребуется шесть ЛЭ: четыре 2И и два 2ИЛИ. В технической реализации по ДНФ из формулы (1.2) требовалось пять элементов: четыре 3И и один 4ИЛИ (см. рис. 1.4). Попробуем ещё раз преобразовать формулу (1.2): Воспользовавшись теоремой №11 Для технической реализации такой МДНФ потребуется четыре ЛЭ: один 3И, один 2И и два 2ИЛИ. Мы получили неоднозначные результаты. С одной стороны по ДНФ пять многовходовых (число входов >2) ЛЭ, с другой стороны по МДНФ шесть простых двухвходовых ЛЭ или четыре ЛЭ, из которых один многовходовый. Окончательный выбор варианта технической реализации будет зависеть от типа заданных (или имеющихся в наличии) ЛЭ. Рассмотренный пример для трёх входных переменных позволил достаточно просто воспользоваться теоремами алгебры логики. Если же входных переменных будет больше, то преобразования становятся не столь очевидными. 2.2. Способ представления ФАЛ с использованием карт Вейча – КарноСпособ представления с использованием карт Вейча – Карно базируется на табличном представлении ФАЛ. Такой способ используется для ручной минимизации, когда количество входных переменных не более пяти. Карта Вейча – Карно – это прямоугольная таблица, число клеток в которой равно 2n, где n – число переменных. Для каждой клетки ставится в соответствие свой набор входных переменных, а в клетке записывается значение функции (0 или 1) на этом наборе. К 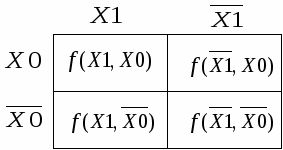 арта для двух входных переменных представлена на рис. 2.1. Она содержит четыре клетки. По краям карты указаны значения входных переменных, которые не изменяются для соответствующих строк и столбцов. Рис. 2.1. Карта Вейча – Карно для функции двух переменных К 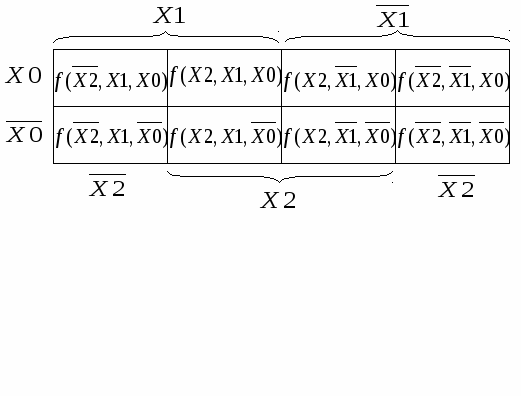 арта для трёх входных переменных представлена на рис. 2.2. Она содержит восемь клеток. Наборы входных переменных крайнего правого и крайнего левого столбцов являются соседними, поэтому пространственно такая карта может быть представлена в виде цилиндра. Рис. 2.2. Карта Вейча – Карно для функции трёх переменных Карта для четырёх входных переменных представлена на рис. 2.3. Она содержит шестнадцать клеток. Наборы входных переменных крайнего правого и крайнего левого столбцов, а также нижней и верхней строк являются соседними, поэтому пространственно такая карта может быть представлена в виде тора. Карта для пяти входных переменных содержит тридцать две клетки. Её можно представить как две карты для четырёх переменных, расположенные одна над другой. Наборы входных переменных крайнего правого и крайнего левого столбцов, а также нижней и верхней строк являются соседними, поэтому пространственно такая карта может быть представлена как два тора, вложенные один в другой. Соседним наборам дополнительно соответствуют клетки, расположенные на разных торах одна под другой. Ввиду сложности работы с такой картой она применяется достаточно редко. Р  ис. 2.3. Карта Вейча – Карно для функции четырёх переменных |
