Курс лекций ТДУ АТ. Курс лекций для студентов специальности 190401 Электроснабжение железных дорог
 Скачать 1.39 Mb. Скачать 1.39 Mb.
|
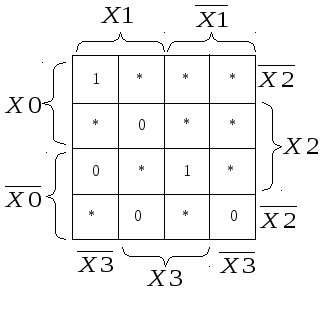
2.3. Минимизация полностью определённой ФАЛПри минимизации ФАЛ с помощью карт Вейча – Карно используются либо единичные, либо нулевые значения функции. В обоих случаях получаются равносильные выражения, которые, однако, могут отличаться по числу ЛЭ и выполняемым логическим операциям. В п.1.5 отмечено, что ФАЛ называется полностью определённой, если заданы все 2n её значений yi. Алгоритм минимизации такой ФАЛ с помощью карт Вейча – Карно следующий: 1) на карте, построенной для ФАЛ, содержащей n-переменных, выделяют прямоугольные области, объединяющие выбранные значения (0 или 1) функции. Каждая область может содержать только 2k клеток, где k – целое число. Выделенные области могут пересекаться, то есть одна или несколько клеток могут принадлежать разным областям. 2) каждой из выделенных областей соответствует самостоятельное логическое произведение входных переменных, значения которых в пределах выделенной области остаются неизменными. Каждое такое произведение содержит (n – k) переменных и называется импликанта. 3) из полученного множества областей выбирают минимальное число максимально больших, включающих в себя все выбранные значения (0 или 1) функции. 4) логически суммируются импликанты, соответствующие выбранным областям. Полученная функция образует МДНФ. При объединении клеток с единичными значениями ФАЛ получается МДНФ самой функции, а при объединении клеток с нулевыми значениями – МДНФ функции, инверсной заданной. Применив к полученной инверсной МДНФ теоремы Де-Моргана можно получить минимальную конъюнктивно нормальную функцию (МКНФ). Рассмотрим пример минимизации ФАЛ, заданной алгебраическим выражением: С 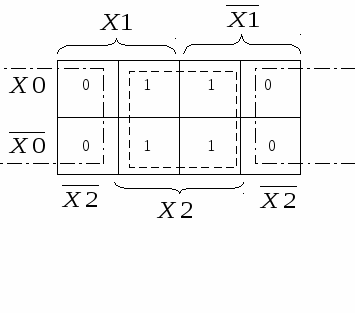 оставим карту Вейча – Карно для заданной ФАЛ. Выделим на карте покрытие, содержащее все единичные значения ФАЛ (выделено пунктиром). Запишем для него значение импликанты, которая будет единственным слагаемым в МДНФ: Y = X2. Если объединить нулевые значения функции (выделено штрих пунктиром), получим МДНФ, инверсную заданной: Рассмотрим другой пример минимизации ФАЛ, заданной алгебраическим выражением [1]: С 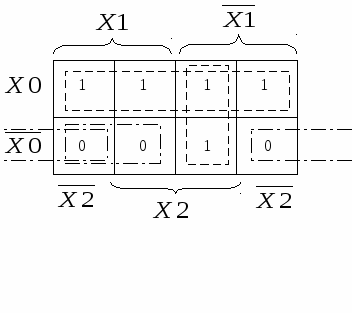 оставим карту Вейча – Карно. Выделим на карте две области, содержащие все единичные значения ФАЛ (выделено пунктиром). Запишем МДНФ как логическую сумму двух импликант: Выделим на карте две области, содержащие все нулевые значения ФАЛ (выделено штрих пунктиром). Запишем МДНФ, инверсную заданной, как логическую сумму двух импликант: Получились равносильные, но разные выражения. Чтобы доказать равносильность выражений, применим к МДНФ, инверсной заданной, теорему Де-Моргана: Применив к данному выражению теорему №10 (см таблицу 1.7), получим ФАЛ Даже из таких простых примеров видно, что при минимизации по единичным и по нулевым значениям получаются равносильные, но не обязательно одинаковые выражения. Техническая реализация таких логических устройств также будет различной. Используя теоремы алгебры логики выражения можно преобразовать к одинаковому виду, однако преобразования могут быть не очевидны. Поэтому при минимизации желательно рассмотреть оба варианта значений функции и постараться получить наиболее простое выражение, которое будет иметь минимальную стоимость технической реализации. 2.4. Минимизация недоопределённой ФАЛФАЛ называется недоопределённой (частично определённой), если часть её значений yi не задана (см. п. 1.5). При минимизации такой ФАЛ необязательным значениям, которые обычно обозначают *, можно произвольно присваивать единичные или нулевые значения из условия получения на карте Вейча Карно минимального числа максимально больших областей. Рассмотрим пример минимизации ФАЛ, заданной таблицей истинности:
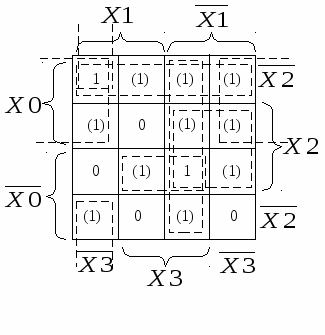
Составим карту Вейча – Карно. Как видно из карты, ни единичные, ни нулевые значения ФАЛ невозможно объединить друг с другом. Поэтому ДНФ имеет вид а КНФ Предположим, что для доопределения ФАЛ принято решение присвоить всем необязательным значениям функции единичные значения. В результате получим следующий вид карты, на которой выделены области единичных значений, и соответствующую МДНФ.
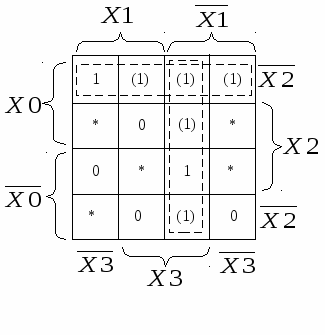
Очевидно, что такое решение привело к отрицательному результату. Полученная МДНФ оказалась даже сложнее исходной ДНФ (2.5). Поэтому проведём новое доопределение ФАЛ, добавив единичные значения функции только для получения на карте Вейча Карно минимального числа максимально больших областей.
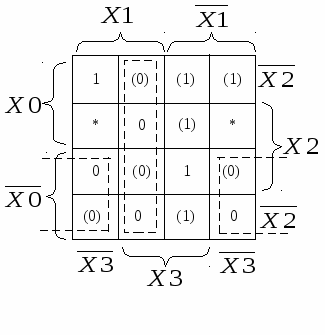
Поскольку выделить область из восьми клеток не удалось, выбрано решение о выделении двух областей из четырёх клеток каждая. Полученное выражение МДНФ проще исходной ДНФ и требует для своей реализации два инвертора, два элемента 2И и один элемент 2ИЛИ. Теперь проведём доопределение ФАЛ, добавив нулевые значения функции только для получения на карте Вейча Карно минимального числа максимально больших областей.
Аналогично выделяем две области по четыре клетки в каждой, поскольку выделить область из восьми клеток невозможно. Полученное выражение для МДНФ, инверсной заданной, также содержит логическую сумму двух логических произведений. Для реализации потребуется три инвертора (два для переменных и один для функции), два элемента 2И и один 2ИЛИ. Для дальнейших преобразований воспользуемся теоремой Де-Моргана: В результате получилось выражение существенно проще, чем исходная КНФ (2.6), для реализации которого потребуется два инвертора, два элемента 2ИЛИ и один элемент 2И. Следует также отметить, что в варианте МКНФ не нужна переменная Х2. Окончательный выбор варианта технической реализации ФАЛ будет зависеть от типа заданных (или имеющихся в наличии) ЛЭ. |