Курс лекций по дисциплине Биомеханика для обучающихся специальности (шифр) 0103000Физическая культура и спорт
 Скачать 0.72 Mb.
|
|
Тема 8.Перемещающиеся движения 1.Полет спортивных снарядов 2.Вращение снаряда и сопротивление воздуха. 3. Сила действия в перемещающих движениях 4.Скорость в перемещающих движениях 5.Точность в перемещающих движениях Перемещающимися в биомеханике называют движения, задача которых – перемещение какого-либо тела (снаряда, мяча, соперника, партнера). Перемещающие движения разнообразны. Примерами в спорте могут быть метания, удары по мячу, броски партнера в акробатике и т. п. К перемещающим движениям в спорте обычно предъявляются требования достичь максимальных величин: а) силы действия (при подъеме штанги), б) скорости перемещаемого тела, (в метаниях), в) точности (штрафные броски в баскетболе). Нередки и случаи, когда эти требования (например, скорости и точности) предъявляются совместно. Среди перемещающих различают движения: а) с разгоном перемещаемых тел (например, метание копья), б) с ударным взаимодействием (например, удары в теннисе или футболе). Поскольку большинство спортивных перемещающих движений связано с сообщением скорости вылета какому-нибудь снаряду (мячу, снаряду для метания), рассмотрим прежде всего механические основы полета спортивных снарядов. Полет спортивных снарядов Траектория (в частности, дальность) полета снаряда определяется: а) начальной скоростью вылета, б) углом вылета, в) местом (высотой) выпуска снаряда, г) вращением снаряда и д) сопротивлением воздуха, которое, в свою очередь, зависит от аэродинамических свойств снаряда, силы и направления ветра, плотности воздуха (в горах, где атмосферное давление ниже, плотность воздуха меньше и спортивный снаряд при тех же начальных условиях вылета может пролететь большее расстояние). Начальная скорость вылета является той основной характеристикой, которая закономерно изменяется с ростом спортивного мастерства. В отсутствие сопротивления воздуха дальность полета снаряда пропорциональна квадрату скорости вылета. Увеличение скорости вылета, скажем, в 1,5 раза должно увеличить дальность полета снаряда в 1,52, т.е. в 2,25 раза. Например, скорость вылета ядра 10 м/с соответствует результату в толкании ядра в среднем 12 м, а скорость 15 м/с – результату около 25 м. У спортсменов международного класса максимальные скорости вылета снарядов равны: при ударе ракеткой (подача в теннисе) и клюшкой (хоккей) – свыше 50 м/с, при ударе рукой (нападающий удар в волейболе) и ногой (футбол), метании копья – около 35 м/с. Из-за сопротивления воздуха скорость в конце полета снаряда меньше начальной скорости вылета. Углы вылета. Различают следующие основные углы вылета: 1. Угол места – угол между горизонталью и вектором скорости вылета (он определяет движение снаряда в вертикальной плоскости: выше – ниже). 2. Азимут – угол вылета в горизонтальной плоскости (правее – левее, измеряется от условно выбранного направления отсчета). 3. Угол атаки – угол между вектором скорости вылета и продольной осью снаряда. Метатели копья стремятся, чтобы угол атаки был близок к нулю («попасть точно в копье»). Метателям диска рекомендуется выпускать диск с отрицательным углом атаки. При полете мячей, ядра и молота угла атаки нет. Высота выпуска снаряда влияет на дальность полета. Дальность полета снаряда увеличивается примерно на столько, на сколько увеличивается высота выпуска снаряда. Вращение снаряда и сопротивление воздуха. Вращение снаряда оказывает двойное влияние на его полет. Во-первых, вращение как бы стабилизирует снаряд в воздухе, не давая ему «кувыркаться». Здесь действует гироскопический эффект, подобный тому, который позволяет не падать вращающемуся волчку. Во-вторых, быстрое вращение снаряда искривляет его траекторию (так называемый эффект Магнуса). Если мяч вращается (такое вращение нередко называют спином, от англ. spin – вращение), то скорость воздушного потока на разных его сторонах будет разной. Вращаясь, мяч увлекает прилегающие слои воздуха, которые начинают двигаться вокруг него (циркулировать). В тех местах, где скорости поступательного и вращательного движений складываются, скорость воздушного потока становится больше; с противоположной стороны мяча эти скорости вычитаются и результирующая скорость меньше. Из-за этого и давление с разных сторон будет разным: больше с той стороны, где скорость воздушного потока меньше. Это следует из известного закона Бернулли: давление газа или жидкости обратно пропорционально скорости их движения (этот закон можно применить к случаю, показанному на рисунке). Эффект Магнуса позволяет, например, выполняя угловой удар в футболе, послать мяч в ворота. Величина боковой силы, действующей на вращающийся мяч, зависит от скорости его полета и скорости вращения. Влияние вращения мяча на его траекторию тем выше, чем больше поступательная скорость. Пытаться придать медленно летящему мячу большое вращение, чтобы влиять на направление полета, нецелесообразно. Теннисные мячи при соответствующих ударах вращаются со скоростью выше 100 об/с, футбольные и волейбольные – значительно медленнее. Если направление вращения мяча совпадает с направлением полета, такой мяч в спортивной практике называют крученым, если не совпадает,- резаным (крученый мяч катился бы по земле в направлении своего полета, а резаный - назад к игроку, пославшему мяч). Е 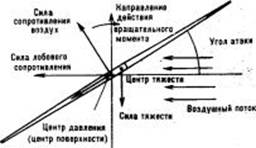 сли воздушный поток обтекает снаряд под некоторым углом атаки, то сила сопротивления воздуха направлена под углом к потоку (рис.97). Эту силу можно разложить на составляющие: одна из них направлена по потоку – это лобовое сопротивление, другая перпендикулярна к потоку – это подъемная сила. Существенно помнить, что подъемная сила не обязательно направлена вверх; ее направление может быть различным. Это зависит от положения снаряда и направления воздушного потока относительно его. В тех случаях, когда подъемная сила направлена вверх и уравновешивает вес снаряда. он может начать планировать. Планирование копья и диска существенно повышает результаты в метании.Если центр давления воздушного потока на снаряд не совпадает с центром тяжести, возникает вращательный момент силы, и снаряд теряет устойчивость. Аналогичная картина и проблема сохранения устойчивости возникают и в полетной фазе в прыжках на лыжах. Отсутствие вращения достигается выбором правильной позы, при которой центр тяжести тела и центр его поверхности (центр давления воздушного потока) расположены так, что вращательный момент не создается. Сила действия в перемещающих движениях Сила действия в перемещающих движениях обычно проявляется конечными звеньями многозвенной кинематической цепи. При этом отдельные звенья могут взаимодействовать двумя способами: 1. Параллельно – когда возможна взаимокомпенсация действия звеньев; если сила, проявляемая одним из звеньев, недостаточна, другое звено компенсирует это большей силой. Пример: при бросках в борьбе недостаточная для выполнения приема мышечная сила одной руки может компенсироваться большей силой действия второй руки. Параллельное взаимодействие возможно лишь в разветвляющихся кинематических цепях (действия двух рук или двух ног). 2. Последовательно – когда взаимокомпенсация невозможна. При последовательном взаимодействии звеньев многозвенной кинематической цепи нередко бывает что какое-то одно звено оказывается более слабым, чем остальные и ограничивает проявление максимальной силы. Очень важно уметь распознавать такое отстающее звено с целью либо его целенаправленно укрепить, либо изменить технику движения таким образом, чтобы данное звено не ограничивало роста результатов. Например, толкатели ядра, у которых мышцы голеностопного сустава и стопы относительно слабые, делают скачок перед финальным усилием с опорой на всю стопу; спортсмены с сильной стопой могут выполнять скачок с приходом на носок. Включение в работу слабых звеньев (если они могут быть выключены) является технической ошибкой, приводящей к снижению спортивного результата. Скорость в перемещающих движениях необходимо определенное сочетание во времени движений отдельных звеньев тела (рис. 100). Каждое из этих звеньев участвует во вращательном движении относительно оси сустава и в поступательном движении этого сустава, которое можно рассматривать как переносное. Например, при ударе ногой по мячу голень перемещается за счет разгибания в коленном суставе (движение по отношению к бедру и коленному суставу) и за счет движения бедра и самого коленного сустава (переносное движение). Вращательное движение звеньев двигательного аппарата человека обусловлено: 1) действием момента силы тяги мышц, проходящих через сустав, например сгибателей и разгибателей его; 2) ускоренным движением самого сустава. Оно вызвано силой, линия действия которой проходит через суставную ось (так называемой суставной силой). Если бы сустав был неподвижен, то, конечно, под действием этой силы движения относительно оси не возникло бы. Ведь нельзя же раскачать качели, надавливая на их ось. Но если ось под действием силы смещается, то подвешенное к ней звено поворачивается вокруг оси. У здорового человека голень при ходьбе движется как за счет движения колена, так и за счет силы тяги мышц коленного сустава. Подобное выполнение вращательного движения в спортивной практике нередко называют «хлестом». Он широко используется в быстрых перемещающих движениях. Выполнение движений «хлестом» основано на том, что проксимальный сустав сначала быстро движется в направлении метания или удара, а затем резко тормозится. Это вызывает быстрое вращательное движение дистального звена тела. На рис. 8.1 показано, как последовательно двигается волна таких отрицательных ускорений от нижних конечностей к верхним при метании. 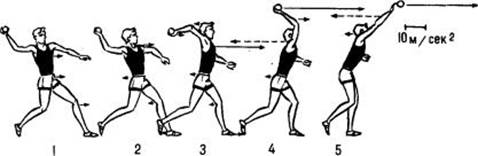 Рис. 8.1. Горизонтальные ускорения основных суставов при метании мяча 150 г (результат 95 м 20 см) (Е. Н. Матвеев). На кадрах 3 и 4, видно, как быстро изменилось ускорение плечевого сустава с положительного на отрицательное При выполнении движений «хлестом» максимумы переносной и относительной скорости не совпадают во времени, т. е. движения выполняют не так. В самом деле, торможение проксимальных звеньев (например, туловища и плеча на рис. 8.1), конечно, снижает их скорость. Однако это повышает скорость (относительную) дистальных звеньев, так что, несмотря на снижение переносной скорости, абсолютная скорость конечного звена, равная сумме переносной и относительной скорости, может оказаться выше. В случае перемещения тел с разгоном (метания, броски и т. п.) увеличение скорости снаряда обычно проходит в три этапа: 1. Скорость сообщается всей системе «спортсмен—снаряд», от чего она приобретает определенное количество движения (разбег в метании копья, повороты при метании диска и молота и т. п.). 2. Скорость сообщается только верхней части системы «спортсмен—снаряд»: туловищу и снаряду (первая половина финального усилия; в это время обе ноги касаются опоры). 3. Скорость сообщается только снаряду и метающей руке (вторая половина финального усилия). Скорость вылета снаряда представляет собой сумму скоростей, приобретенных им на каждом из этих этапов. Однако векторы скоростей стартового и финального разгонов обычно не совпадают по направлению, поэтому их суммирование может быть только геометрическим (по правилу параллелограмма). Значительная часть стартовой скорости теряется. Например, сильнейшие толкатели ядра могут толкнуть ядро с места на 19 м, что соответствует скорости вылета снаряда около 13 м/с. В скачке они сообщают ядру скорость до 2,5 м/с. Если бы эти скорости удалось сложить арифметически, то скорость вылета ядра была бы равна 13 + 2,5 —15,5 м/с, что дало бы результат около 26 м — примерно на 4 м выше мирового рекорда. Для увеличения скорости вылета снаряда стремятся увеличить путь воздействия на него в финальном усилии. Например, у сильнейших в мире толкателей ядра — финалистов олимпийских игр — расстояние между ядром и землей на старте уменьшилось со 105 см в 1960 г. до 80 см в 1976 г. Для увеличения пути воздействия на снаряд используют так называемый обгон звеньев. Точность в перемещающих движениях Под точностью движения понимают степень его близости требованиям двигательного задания. Вообще говоря, любое движение может быть выполнено лишь в том случае, если оно достаточно точно. Если, например, во время ходьбы человек будет выполнять движения очень неточно, то идти он не сможет. Однако здесь будет идти речь о точности в более узком смысле слова - о точности рабочего звена тела (например, кисти) или управляемого этим звеном снаряда (фехтовального оружия, мяча, ручки для письма). Различают два вида точностных заданий. В первом необходимо обеспечить точность движения на всей его траектории (пример - обязательная программа в фигурном катании на коньках, где требуется, чтобы след конька был идеальной геометрической фигурой). Такие двигательные задания называют задачами слежения. Во втором виде заданий неважно, какова траектория рабочей точки тела или снаряда, необходимо лишь попасть в обусловленную цель (в мишень, ворота, поражаемую часть тела противника и т. п.). Такие двигательные задачи называют задачами попадания, а точность - целевой точностью. Целевая точность характеризуется величиной отклонения от цели. В зависимости от конкретного вида двигательного задания используют различные способы оценки точности. Если стоит, например, задача бросить мяч на определенное расстояние и ошибка может выражаться только в перелете или недолете (отклонения вправо или влево значения не имеют), то при большом числе бросков мяч будет приземляться, конечно, не в одно и то же место. При этом средняя точка попадания может отклоняться от центра мишени. Это отклонение называется систематической ошибкой попадания. Кроме того, места приземления мяча будут как-то рассеяны относительно средней точки попадания. Из баллистики известно, что это рассеивание подчиняется закону нормального распределения. Нормальное распределение характеризуется средней величиной и стандартным (средним квадратическим) отклонением. Стандартное отклонение указывает величину случайной ошибки попадания. Величина, обратная стандартному отклонению, называется кучностью попадания. Систематическая ошибка и кучность вместе характеризуют целевую точность. Если систематическая ошибка равна нулю, т. е. если спортсмен попадает в центр мишени, целевая точность характеризуется только кучностью. Когда имеют значения отклонения от центра мишени не только, вперед-назад (вверх-вниз), но и вправо-влево, например в пулевой стрельбе или при ударах по воротам, различают вертикальную и горизонтальную точность. Для оценки каждой из них надо знать систематическую и случайную ошибки, т. е. Всего четыре показателя. Часто более удобно оценивать точность по числу удачных попыток — попаданий в цель. Если систематическая ошибка известна (в частности, если она равна нулю), то, пользуясь статистическими таблицами -нормального распределения, по проценту попаданий легко вычислить величину стандартной ошибки. Отклонения от центра мишени вправо и влево зависят от азимута, а отклонения вперед-назад (вверх-вниз) — от угла места и скорости вылета снаряда. При этом снаряд попадает в цель лишь при строго определенном сочетании угла и скорости вылета. Изменение одной из этих характеристик при постоянном значении второй приводит к промаху. Исследования показывают, что главная трудность в достижении высокой целевой точности как раз и состоит в том, чтобы обеспечить правильное сочетание угла и скорости вылета. Например, отклонения (дисперсия) начальных характеристик вылета мяча — угла и скорости — у баскетболистов-"снайперов" такие же, как у тех, кто не отличается высокой точностью бросков. Но у первых избранный угол вылета соответствует скорости, а у вторых такого соответствия нет. В достижении высокой целевой точности существенную роль играет техника выполнения упражнения, в частности такая организация движений, при которой облегчается исправление ошибок, допущенных по ходу попытки. Поскольку подобная коррекция происходит до того, как становится ясен итоговый результат действия, ее называют предварительной или прелиминарной (от лат. pre – перед и limin – порог) коррекцией. Например, при выполнении баскетбольных бросков с разных дистанций большая часть скорости вылета мяча создается движением ног, руки же обеспечивают тонкие корректирующие добавки. 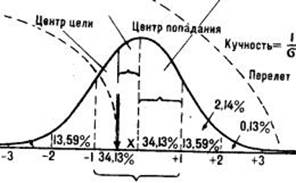 Рис. 8.2. Показатели, используемые при оценке целевой точности. Показан также процент попаданий при отклонении снаряда на разные расстояния от центра попадания (кривая нормального распределения) Особенно трудно добиться необходимой точности при ударных действиях. Например, в футболе при ударе с 20 м достаточно ошибиться в точке приложения удара всего на 1 см, чтобы мяч отклонился от цели почти на 2 м. Поэтому более точны те удары, которые выполняются при относительно большой площади соприкосновения с мячом. Так, при ударах внутренней стороной стопы («щечкой») легче добиться необходимой точности, чем при ударах носком. Наиболее трудно добиться высокой точности при ударах по движущемуся мячу («в одно касание»). Биомеханическая основа этих, затруднений состоит в следующем. Мяч, ударяясь о плоскость под определенным углом, отскакивает от нее примерно под тем же углом. Следовательно, если подставить, например, ракетку под мяч вертикально на разных участках его траектории, то он отразится по-разному (рис. 8.2). Чтобы отразить мяч в нужном направлении (не ударяя по нему), нужно подставить плоскость ракетки (или ноги) перпендикулярно к линии, делящей угол между направлениями полета мяча до и после отскока примерно пополам. При ударных действиях к первоначальной скорости мяча добавляется скорость, привносимая ударом. Они складываются геометрически (по правилу параллелограмма). В результате оказывается, что мяч после удара движется не в направлении действия силы удара. Мяч попадает в цель лишь в том случае, если направление и сила удара будут строго соответствовать направлению и скорости летящего мяча. Добиться такого соответствия трудно. Целевая точность снижается при значительном увеличении скорости движений. Небольшие колебания скорости от попытки к попытке на точность попадания в цель не влияют. Целевая точность зависит также от расстояния и направления до цели. |