Курс лекций по дисциплине Эконометрика
 Скачать 2.09 Mb.
|
3. Классическая линейная модель множественной регрессииРассмотрим обобщение линейной регрессионной модели для случая более двух переменных. Всякий раз, когда изучаемый процесс или явление является результатом совместного действия нескольких факторов, у исследователя возникает потребность в оценке влияния каждого фактора в отдельности. Один из стандартных методов3, позволяющий успешно решить эту задачу, сутьмножественная регрессия. 3.1. Предположения моделиПусть мы располагаем выборочными наблюдениями над k переменными Yi и  , j=1,..., k, i=1,2,…,n, где n – количество наблюдений:
Предположим, что существует линейное соотношение между результирующей переменной Yи k объясняющими переменными X1, X3, ..., Xk. Тогда с учетом случайной ошибки ui запишем уравнение:  (3.1)В (3.1) неизвестны коэффициенты  , j=0,2,…,kи параметры распределения ui. Задача состоит в оценивании этих неизвестных величин. Модель (3.1) называется классической линейной моделью множественной регрессии (КЛММР). Заметим, что часто имеют в виду, что переменная X0 при 0 равна единице для всех наблюдений i=1,2,…,n. Относительно переменных модели в уравнении (3.1) примем следующие основные гипотезы: E(ui)=0; (3.2) 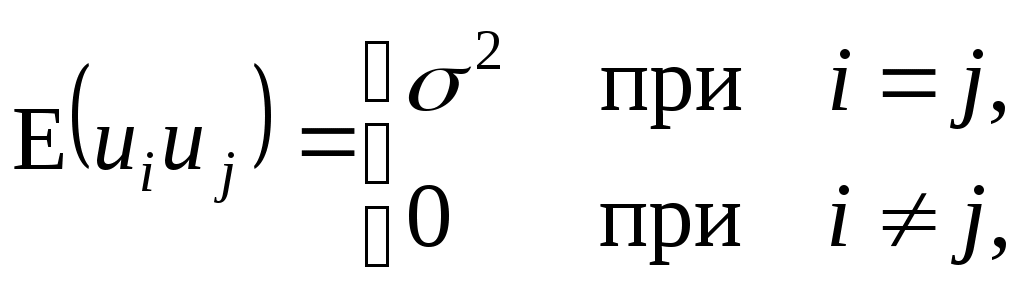 (3.3)X1, X3, ..., Xk – неслучайные переменные; (3.4) Не должно существовать строгой линейной зависимости между переменными X1, X3, ..., Xk. (3.5) Первая гипотеза (3.2) означает, что переменные ui имеют нулевую среднюю. Суть гипотезы (3.3) в том, что все случайные ошибки ui имеют постоянную дисперсию, то есть выполняется условие гомоскедастичности дисперсии (см. подробнее раздел 4). Согласно (3.4) в повторяющихся выборочных наблюдениях источником возмущений Y являются случайные колебания ui, а значит, свойства оценок и критериев обусловлены объясняющими переменными X1, X3, ..., Xk. Последняя гипотеза (3.5) означает, в частности, что не существует линейной зависимости между объясняющими переменными, включая переменную X0, которая всегда равна 1. Понятно, что условия (3.2)-(3.4) соответствуют своим аналогам для случая двух переменных в п.2.2. |