Курс лекций по дисциплине Эконометрика
 Скачать 2.09 Mb.
|
|
Часто эконометрист сталкивается с ситуацией, когда к уже имеющейся выборке он хочет присоединить небольшую дополнительную порцию данных, но не знает, можно ли считать выборки регрессионно однородными. Если необходимо выяснить, можно ли использовать одну и ту же модель для двух разных выборок данных или следует оценивать отдельные регрессии для каждой выборки, то можно воспользоваться тестом Чоу. Рассмотрим модели:  (4.14) (4.15)Мы хотим проверить гипотезу H0:  ,которая содержательно означает, что для двух имеющихся выборок из n1 и n2 наблюдений можно использовать одну и ту же регрессионную модель, т.е. выборки можно объединить. Процедура Чоу для статистической проверки гипотезы H0 суть: 1. Строим МНК оценки регрессии (4.14) и вычисляем сумму квадратов остатков, которую обозначим  . Строим МНК оценки регрессии (4.15) и вычисляем сумму квадратов остатков, которую обозначим  .2. Строим МНК оценки регрессии по объединенной (общей) выборке, содержащей в себе все наблюдения (числом n1+n2) обеих выборок и вычисляем сумму квадратов остатков, которую обозначим er. 3. Критическая статистика F вычисляется по формуле: 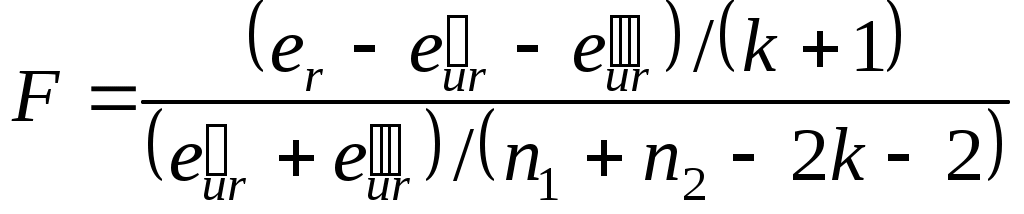 и имеет распределение Фишера с (k+1) и (n1+n22k2) степенями свободы. Если F > F, то нулевая гипотеза отвергается, и в этом случае мы не можем объединить две выборки в одну. 5. Временные ряды 5.1.Специфика временных рядов Часто исследователь имеет дело с данными в виде временных рядов. Совокупность наблюдений  анализируемой величины  , произведенных в последовательные моменты времени  , называется временным рядом. Иначе говоря, временной ряд – это упорядоченная во времени последовательность наблюдений. Среди временных рядов выделяют одномерные, полученные в результате наблюдения одной, фиксированной характеристики исследуемого объекта, и, многомерные временные ряды как результат наблюдений нескольких характеристик одного исследуемого объекта в течение ряда моментов времени. По времени наблюдения временные ряды делятся на дискретные и непрерывные. Дискретные ряды, в свою очередь, разделяются на ряды с равноотстоящими и произвольными моментами наблюдения. Временные ряды бывают детерминированными и случайными: первые получены как значения некоторой неслучайной функции, а вторые - как реализации случайной величины. Стохастические временные ряды подразделяются на стационарные и нестационарные. Ряд y(t) называется стационарным (в узком смысле), если среднее, дисперсия и ковариации y(t) не зависят от t. В дальнейшем, если не оговорено иначе, будем рассматривать одномерные, дискретные с равноотстоящими моментами наблюдений случайные временные ряды. Природа временных рядов существенно отличается от природы пространственных данных, что проявляется в весьма специфических свойствах временных рядов. В своей работе исследователь должен учитывать эти особенности, основные из которых отображены в таблице 5.1. Таблица 5.1 Особенности временных рядов
| ||||||||||||||||||||