Курс лекций по дисциплине Эконометрика
 Скачать 2.09 Mb.
|
Множественный коэффициент корреляциии множественный коэффициент детерминацииМножественный коэффициент корреляции используется в качестве меры степени тесноты статистической связи между результирующим показателем (зависимой переменной) y и набором объясняющих (независимых) переменных  или, иначе говоря, оценивает тесноту совместного влияния факторов на результат. Множественный коэффициент корреляции может быть вычислен по ряду формул5, в том числе: с использованием матрицы парных коэффициентов корреляции  , (3.18)где r - определитель матрицы парных коэффициентов корреляции y, , r11 - определитель матрицы межфакторной корреляции ;стандартизованных коэффициентов регрессии  и парных коэффициентов корреляции   . (3.19)Для модели, в которой присутствуют две независимые переменные, формула (3.18) упрощается 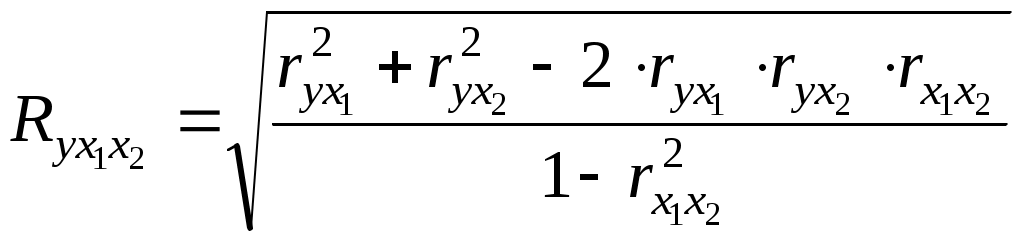 . (3.20)Квадрат множественного коэффициента корреляции равен коэффициенту детерминации R2. Как и в случае парной регрессии, R2 свидетельствует о качестве регрессионной модели и отражает долю общей вариации результирующего признака y, объясненную изменением функции регрессии f(x) (см. 2.4). Кроме того, коэффициент детерминации может быть найден по формуле 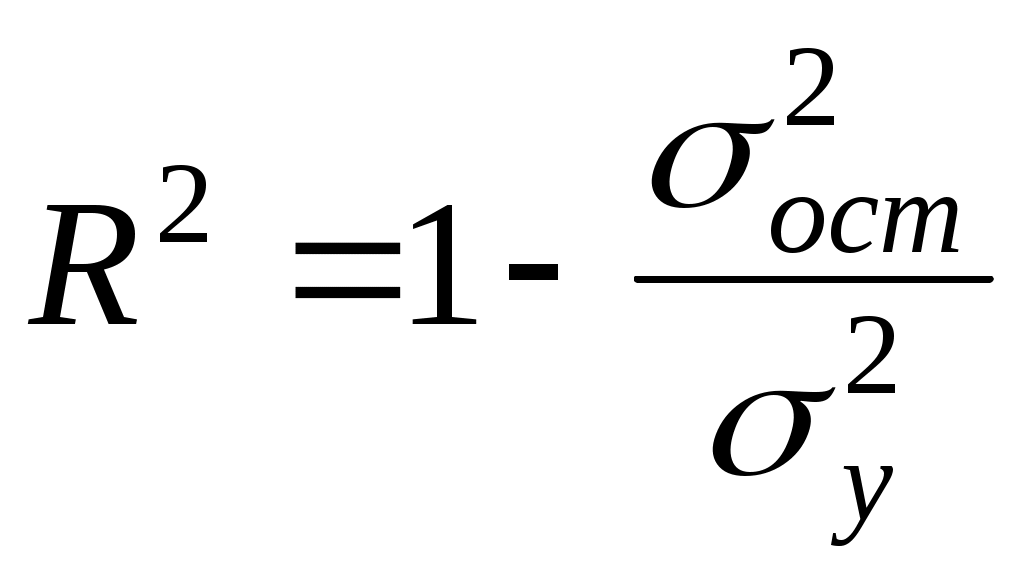 . (3.21) Однако использование R2 в случае множественной регрессии является не вполне корректным, так как коэффициент детерминации возрастает при добавлении регрессоров в модель. Это происходит потому, что остаточная дисперсия уменьшается при введении дополнительных переменных. И если число факторов приблизится к числу наблюдений, то остаточная дисперсия будет равна нулю, и коэффициент множественной корреляции, а значит и коэффициент детерминации, приблизятся к единице, хотя в действительности связь между факторами и результатом и объясняющая способность уравнения регрессии могут быть значительно ниже. Для того чтобы получить адекватную оценку того, насколько хорошо вариация результирующего признака объясняется вариацией нескольких факторных признаков, применяют скорректированный коэффициент детерминации  (3.22)Скорректированный коэффициент детерминации всегда меньше R2. Кроме того, в отличие от R2, который всегда положителен,  может принимать и отрицательное значение.Пример (продолжение примера 1). Рассчитаем множественный коэффициент корреляции, согласно формуле (3.20):  =0,8601.Величина множественного коэффициента корреляции, равного 0,8601, свидетельствует о сильной взаимосвязи стоимости перевозки с весом груза и расстоянием, на которое он перевозится. Коэффициент детерминации равен: R2=0,7399. Скорректированный коэффициент детерминации рассчитываем по формуле (3.22):  =0,7092.Заметим, что величина скорректированного коэффициента детерминации отличается от величины коэффициента детерминации. Таким образом, 70,9% вариации зависимой переменной (стоимости перевозки) объясняется вариацией независимых переменных (весом груза и расстоянием перевозки). Остальные 29,1% вариации зависимой переменной объясняются факторами, неучтенными в модели. Величина скорректированного коэффициента детерминации достаточно велика, следовательно, мы смогли учесть в модели наиболее существенные факторы, определяющие стоимость перевозки. 3.5. Оценка качества модели множественной регрессии Проверка качества модели множественной регрессии может быть осуществлена с помощью дисперсионного анализа. Как уже было отмечено (см. 2.5), сумма квадратов отклонений от среднего в выборке равна сумме квадратов отклонений значений  , полученных по уравнению регрессии, от выборочного среднего  плюс сумма квадратов отклонений Y от линии регрессии . С учетом (3.21) получим таблицу дисперсионного анализа (табл. 3.4), аналог таблицы 2.3. Проверка качества модели множественной регрессии в целом может быть осуществлена с помощью F-критерия Фишера. Для проверки гипотезы о том, что линейная связь между  и yотсутствует:  ,воспользуемся соотношением  (3.23)которое удовлетворяет F - распределению Фишера с (k, n-(k+1)) степенями свободы. Критические значения этой статистики F для уровня значимости затабулированы. |