Курс лекций по дисциплине Эконометрика
 Скачать 2.09 Mb.
|
Y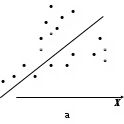  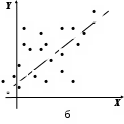 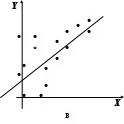 Рис. 4.1. Примеры гетероскедастичности Гетероскедастичность дисперсии случайного члена означает, что 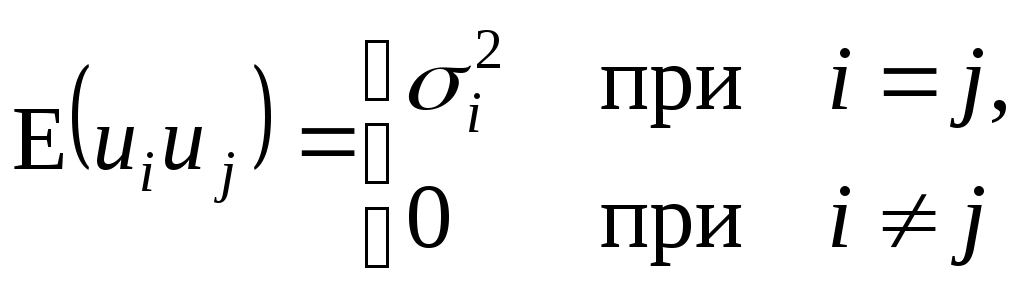 , (4.8)т.е. нарушается предположение (3.3) в КЛММР, и мы должны рассматривать ОЛММР с нулевой ковариацией случайных ошибок (ср. (4.5) и (4.8)). Основные последствия гетероскедастичности проявляются в получении неэффективных оценок МНК и занижении стандартных ошибок коэффициентов регрессии, что завышает t-статистику и дает неправильное представление о точности уравнения регрессии. Поэтому для оценивания регрессии с гетероскедастичными случайными ошибками применяется ОМНК. Предположим, что нам известны значения величин  i =1,…,n. Тогда уравнение (4.3) разделим на i: ,и получим регрессию с постоянной (гомоскедастичной) дисперсией случайного члена, действительно 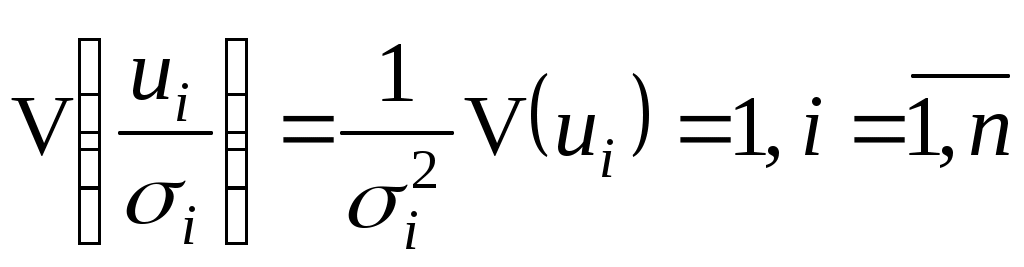 . Для получения оценок неизвестных дисперсий i =1,…,nбудем предполагать, что они пропорциональны некоторым числам, т.е.  , где 2 – некоторая константа.Принимая различные гипотезы относительно характера гетероскедастичности, будем иметь соответствующие значения i. Если дисперсия случайного члена пропорциональна квадрату регрессора X, так что  , то  , i =1,…,n. Если дисперсия случайного члена пропорциональна X, так что 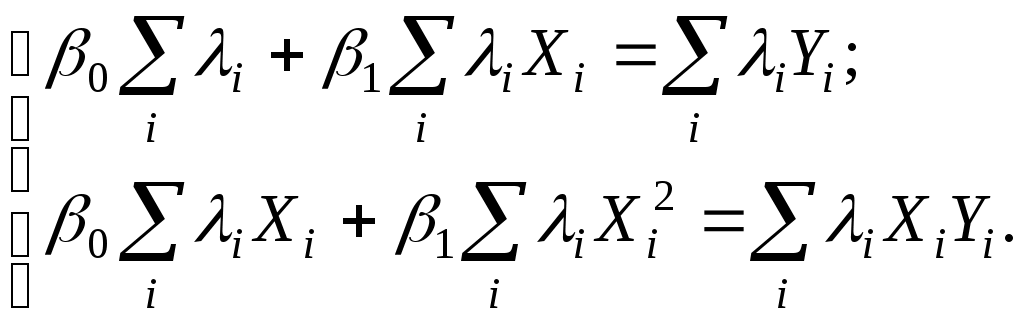 , то  , i =1,…,n. Например, для случая одной объясняющей переменной имеем в этом случае систему уравнений ОМНК вида: Поскольку значения i, i =1,…,n являются фактически весами, которые устраняют неоднородность дисперсии, то ОМНК для системы с гетероскедастичностью часто называют методом взвешенных наименьших квадратов. Существуют также и другие методы коррекции модели на гетероскедастичность, в частности состоятельное оценивание стандартных ошибок. Известны способы коррекции стандартных ошибок Уайта и Невье-Веста [5, с. 144-146]. О проверке выборки на гомоскедастичность. Рассмотрим вопрос тестирования выборки на наличие гомоскедастичности. Возможности такой проверки зависят от природы исходных данных. Если имеется обширная выборка, то можно воспользоваться стандартным критерием однородности дисперсии Бартлетта. Расчленяя выборку на m независимых групп (каждой из них соответствует единственное значение переменной X), вычислим величины: 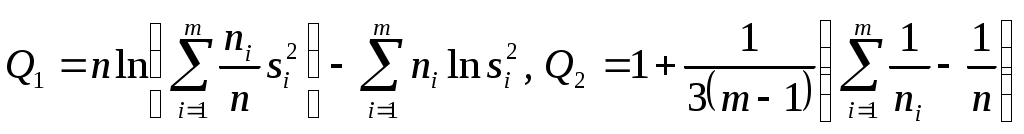 , причем ni=n, здесь ni - число наблюдений в i группе,  - дисперсия ошибки в i группе. Величина Q1/Q2 будет приближенно удовлетворять распределению 2 с (m-1) степенями свободы. Если вычисленное по выборке значение 2 меньше критического, то гипотеза об однородности выборочной дисперсии принимается, в противном случае отклоняется. В случаях малого количества наблюдений в выборке, когда группировка данных невозможна, используется тест Голдфелда и Куандта. Он предусматривает осуществление следующих шагов: 1. Упорядочить наблюдения по убыванию той независимой переменной, относительно которой есть подозрение на гетероскедастичность. 2. Опустить v наблюдений, оказавшихся в центре (v должно быть примерно равно четверти общего количества наблюдений n). 3. Оценить отдельно обыкновенным методом наименьших квадратов регрессии на первых (n-v)/2 наблюдениях и на последних (n-v)/2 наблюдениях при условии, что (n-v)/2 больше числа оцениваемых параметров k. 4. Пусть e1 и e2 - суммы квадратов остатков от первой и второй регрессий соответственно. Тогда статистика Q=e1/e2 будет удовлетворять F - распределению с ((n-v-2k)/2; (n-v-2k)/2) степенями свободы. При Q< F гипотеза об однородности выборочной дисперсии принимается, в противном случае (с ростом величины Q) отклоняется. Очевидно, что решающим для этого теста является выбор величины v. Слишком большое значение v уменьшает надежность теста. Экспериментально авторами теста установлено, что для одной объясняющей переменной оптимальное v=8 при n=30 и v=16 при n=60. Кроме перечисленных, могут использоваться тесты на гетероскедастичность Уайта, Бреуша-Пагана и др. Пример. Проверим по критерию Бартлетта данные из примера 1 раздела 3. Будем иметь табл. 4.1. В табл. 4.1 учтено, что среднее значение ei равно 0, а значит,  . Примем m=2. Тогда:Q1=20ln(10/20167,41 + 10/2059,69) (10ln(167,41)+10ln(59,69))=2,55; Q2=1+1/3(1/10+1/10-1/20)=1,05; Q1/Q2=2,43. При одной степени свободы критическое значение 2 при 5% уровне значимости равно 3,84, а следовательно, гипотеза об однородности выборочной дисперсии принимается. Для тех же данных применим тест Гольдфельда и Куандта. В нашем случае число объясняющих переменных k=2, количество исходных данных в выборке n=20. Упорядочим наблюдения по убыванию независимой переменной X2 – расстояние перевозки, относительно которой есть подозрение на гетероскедастичность. Опустим 4 наблюдения, оказавшихся в центре, т.е. v=4. При значении v=4 получим суммы квадратов остатков от первой и второй регрессий соответственно e1=1167,38 и e2=31,49. Статистика Q=e1/e2=1167,38/31,49 = 37,07 удовлетворяет F-распределению с (6; 6) степенями свободы. F0,05(6, 6) = 4,28, Q > F и гипотеза об однородности выборочной дисперсии должна быть отвергнута. Поскольку тесты дают противоположные результаты (что не редкость в эконометрике), то лучше согласиться с наихудшим вариантом, т.е. предположить наличие гетероскедастичности и предпринять соответствующие корректирующие меры. В частности, скорректировать стандартные ошибки по формуле Невье-Веста. В таблице 4.2 представлены результаты регрессии до корректировки и после корректировки на гетероскедастичность. Видно, что на величине коэффициентов регрессии корректировка на гетероскедастичность не отражается, а стандартные ошибки и значения статистик были пересчитаны. Таблица 4.1 Проверка гомоскедастичности дисперсии по критерию Бартлетта
Таблица 4.2
4.4. Линейная модель множественной регрессии с автокорреляцией остатков Вернемся еще раз к предположению (3.3). Из него, в частности, следует, что ковариации случайной ошибки для разных наблюдений равны нулю. Если к тому же случайные ошибки распределены нормально, то это означает их попарную независимость. Однако регрессионные модели в экономике часто содержат стохастические зависимости между значениями случайных ошибок – автокорреляцию ошибок. Ее причинами являются: во-первых, влияние некоторых случайных факторов или опущенных в уравнении регрессии важных объясняющих переменных, которое не является однократным, а действует в разные периоды времени; во-вторых, случайный член может содержать составляющую, учитывающую ошибку измерения объясняющей переменной. Применение к модели с автокорреляцией остатков обыкновенного МНК приведет к следующим последствиям: 1. Выборочные дисперсии полученных оценок коэффициентов будут больше по сравнению с дисперсиями по альтернативным методам оценивания, т.е. оценки коэффициентов будут неэффективны. 2. Стандартные ошибки коэффициентов будут оценены неправильно, чаще всего занижены, иногда настолько, что нет возможности воспользоваться для проверки гипотез соответствующими точными критериями – мы будем чаще отвергать гипотезу о незначимости регрессии, чем это следовало бы делать в действительности. 3. Прогнозы по модели получаются неэффективными. На практике исследователь в этом случае поставлен перед проблемой тестирования наличия в модели автокорреляции, а также выявления причины автокорреляции при ее обнаружении: или в модели опущена существенная переменная, или структура ошибок зависит от времени. То есть, исследование остатков позволяет судить о правильности модели и ее пригодности для прогнозирования. Простейшим способом проверки наличия автокорреляции является графическое изображение остатков ei. Возможно построение: графика временной последовательности, если остатки получены в разные моменты времени; графика зависимости остатков от значений  , полученных по регрессии;графиков зависимости остатков от объясняющих переменных. Если изображение остатков представляет собой горизонтальную полосу, это указывает на отсутствие каких-либо проблем, связанных с моделью. В противном случае в зависимости от вида и типа графика можно получить информацию о: неадекватности модели, ошибочности расчетов, необходимости включения в модель линейного или квадратичного члена от времени; наконец о непостоянстве дисперсии. Ясно, что ошибки могут коррелировать по-разному, однако без нарушения общности можно рассматривать так называемую сериальную корреляцию (автокорреляцию), когда зависимость между ошибками, отстоящими на некоторое количество шагов s, называемое порядком корреляции (в частности, на один шаг, s=1), остается одинаковой, что хорошо проявляется визуально на графике в системе координат (ei; ei-s). Например, для s=1 на рис. 4.2 показаны отрицательная (слева) и положительная (справа) автокорреляция остатков. В экономических исследованиях чаще всего встречается положительная автокорреляция. 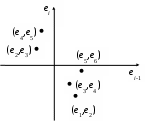 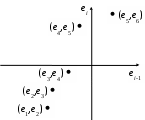 Рис. 4.2. Автокорреляция остатковБолее достоверным способом проверки существования автокорреляции является применение статистических критериев. Хорошо известны два – критерий знаков (относится к непараметрическим критериям) и критерий Дарбина-Уотсона. Для проведения проверки по критерию знаков необходимо расположить остатки ei во временной последовательности, выписать их знаки, подсчитать число образующихся при этом серий nu из одинаковых знаков, а также n1 – число остатков со знаком плюс и n2 – число остатков со знаком минус. Далее определяется вероятность Pr(nu) появления nu групп при нулевой гипотезе – последовательность остатков полностью случайна (автокорреляция отсутствует). Если Pr(nu) < 1–, где – уровень доверия, то нулевая гипотеза отвергается. Для ускорения расчетов для выборок с n1, n2 не больше 20 составлены таблицы с критическими значениями nu при уровне доверия =0,05. Для больших выборок истинное распределение ошибок достаточно точно аппроксимируется нормальным со средним =2n1n2/(n1+n2)+1 и дисперсией 2=2n1n2(2n1n2 – n1 – n2)/(n1 + n2)2/(n1 + n2 – 1), а величина z=(u– + 0,5)/ подчиняется нормированному нормальному распределению, следовательно, критические значения nu могут быть вычислены по формулам (+ z) и (– z), где z определяется из условия 0(z)=(1–)/2 (значения  даны в справочниках).Пример. Получены остатки 0,6; 1,9; –1,8; –2,7; –2,9; 1,4; 3,3; 0,3; 0,8; 2,3; –1,4; –1,1, которые обнаруживают следующую последовательность знаков + + – – – + + + + + – –. Имеем nu=4, n1=7, n2=5. По таблице находим критические значения для nu: 3 и 11. Так как 3 < nu < 11, то нулевая гипотеза принимается, то есть остатки независимы и автокорреляция отсутствует. Критерий знаков достаточно прост и не использует информацию о величине ei, и поэтому недостаточно эффективен. Для проверки гипотезы о существовании линейной автокорреляции первого порядка, которая чаще всего имеет место на практике, предпочтителен критерий Дарбина-Уотсона, основанный на статистике: 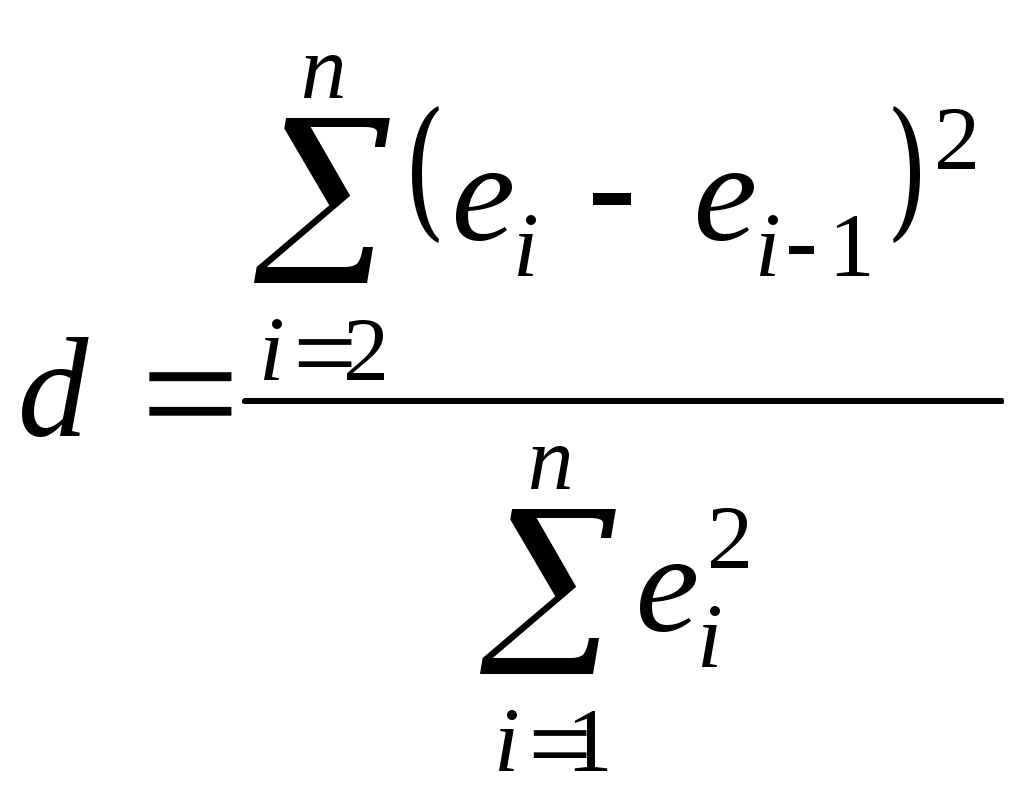 (4.9)Значения первых разностей ошибки в (4.9) будут обнаруживать тенденцию к уменьшению по абсолютной величине по сравнению с абсолютными значениями ei при положительной автокорреляции и к увеличению при отрицательной автокорреляции. Для статистики d имеются верхний dU и нижний dL пределы уровня значимости. Различные статистические решения для нулевой гипотезы H0: автокорреляция равна нулю, даны в табл. 4.3. При этом появляются области неопределенности, так как величина ei зависит не только от значений u, но и от значений последовательных X. Следует отметить, что критерий Дарбина-Уотсона предназначен для моделей с детерминированными (нестохастическими) регрессорами X и не применим, например, в случаях, когда среди объясняющих переменных есть лаговые значения переменной Y. Таблица 4.3 Области статистических решений для критерия Дарбина-Уотсона
Пример. Для примера 1 из п. 3.2 n=20, k=2 имеем табл. 4.4. Далее по формуле (4.9) d=4397,66/2050,37=2,14. Значения dL и dU при уровне значимости 5% получим из справочника при n=20 и k=2: dL=1,10, dU=1,54. Так как d>2, то вычисляем 4–dU=2,46 и 4–dL=2,90 и 2<d<4–dU. Согласно табл. 4.3 гипотеза о равенстве нулю автокорреляции принимается. Какой бы тест на автокорреляцию не использовался, необходимо помнить, что рекомендуется в случаях неопределенности (см. табл. 4.3) принимать гипотезу о наличии автокорреляции, поскольку это гарантирует от отрицательных последствий автокорреляции. В случаях же некорректного принятия гипотезы о равенстве нулю автокорреляции получаем модель, которая не может иметь удовлетворительного применения, хотя формально проходит все проверки. Таблица 4.4 Вычисление значения статистики d
Рассмотрим методы оценивания уравнения регрессии при наличии автокорреляции остатков. Пусть имеем обобщенную линейную модель множественной регрессии в виде (4.3)-(4.7) с гомоскедастичными остатками  .Предположим, что остатки ui удовлетворяют следующему уравнению: ui=ui-1+i, i=2,...,n, (4.10) представляющему собой авторегрессионную модель первого порядка, для которой выполнено ||1, а i удовлетворяют условиям: E(i)=0; 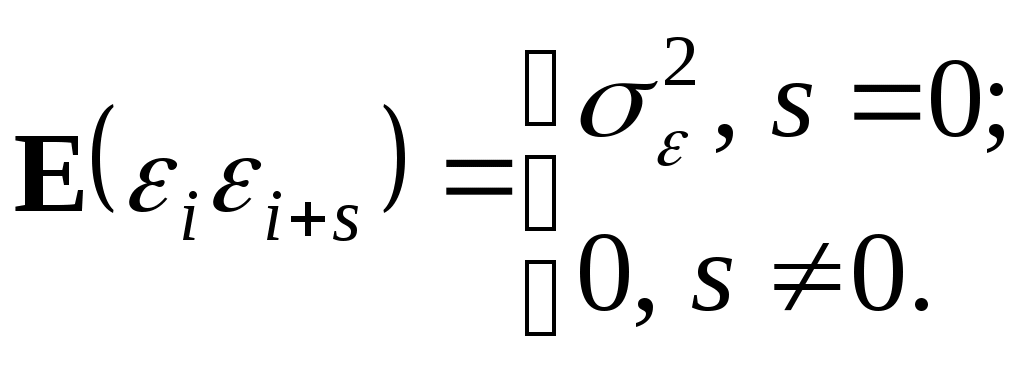 (4.11)Тогда несложно показать, что будет выполняться: 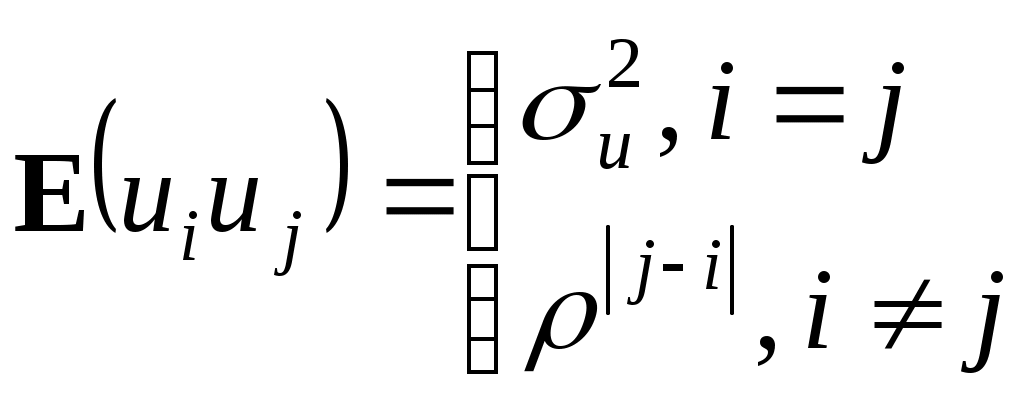 . (4.12)Условие (4.12) является аналогом (4.5) и фактически означает гомоскедастичность дисперсии случайного члена (первая строчка) и автокорреляцию первого порядка (вторая строчка). Ясно, что если бы было известно значение в (4.10) и затем в (4.12), то можно было бы применить ОМНК (элементы матрицы в этом случае вычисляются согласно (4.12)) и получить эффективные оценки коэффициентов регрессии. Однако на практике значение в большинстве случаев не известно, поэтому используются следующие методы оценивания регрессионной модели. Метод 1. Отказавшись от определения величины , являющейся узким местом модели, статистически, можно положить =0,5; 1 или -1. Однако даже грубая статистическая оценка будет, видимо, более эффективной, поэтому другой способ определения с помощью статистики Дарбина-Уотсона 1–0,5d. Применяя затем непосредственно ОМНК, получим оценки коэффициентов. Метод 2. Если значение в (4.12) задано, то альтернативная схема отыскания оценок коэффициентов модели множественной регрессии суть (в целях упрощения, не нарушая общности, иллюстрация метода дана для случая парной регрессии): а) Запишем уравнение модели для случая i и i–1:   .Вычтем из обеих частей первого уравнения умноженное на второе уравнение:  или переобозначив:  с учетом (4.10)  , получим модель  , (4.13)для случайного члена которой выполняется условие (4.11), т.е. автокорреляция отсутствует. При указанном преобразовании первое наблюдение умножается на  , т.е.  ,  .б) Применяем обыкновенный МНК к модели (4.13). В общем случае мы не располагаем информацией о порядке автокорреляции и значениях параметров в авторегрессионном уравнении, а значит, и методы 1 и 2 не дадут искомого результата. Тем не менее, оценки коэффициентов можно найти приближенно с помощью следующих методов (опять в целях упрощения, не нарушая общности, иллюстрация методов дана для случая парной регрессии). Метод 3. Итеративная процедура Кохрейна-Оркатта. а) Оценивается регрессия с исходными не преобразованными данными с помощью обыкновенного МНК.б) Вычисляются остатки ei. в) Оценивается регрессия ei=ei-1+i, и коэффициент при ei-1 дает оценку . г) С учетом полученной оценки уравнение преобразовывается к виду (4.13), оценивание которого позволяет получить пересмотренные оценки коэффициентов 0 и 1.д) Вычисляются остатки регрессии (4.13) и процесс выполняется снова, начиная с этапа в). Итерации заканчиваются, когда абсолютные разности последовательных значений оценок коэффициентов 0, 1 и будут меньше заданного числа (точности). Подобная процедура оценивания порождает проблемы, касающиеся сходимости итерационного процесса и характера найденного минимума: локальный или глобальный. Метод 4. Метод Хилдрета-Лу основан на тех же принципах, что и рассмотренный метод 3, но использует другой алгоритм вычислений. Здесь регрессия (4.13) оценивается МНК для каждого значения из диапазона [-1, 1] с некоторым шагом внутри него. Значение, которое дает минимальную стандартную ошибку для преобразованного уравнения (4.13), принимается в качестве оценки , а коэффициенты регрессии определяются при оценивании уравнения (4.13) с использованием этого значения. Метод 5. Дарбиным была предложена простая схема, дающая эффективные оценки коэффициентов: а). Подставляя (4.10) в модель Yi=0+1Xi+ui, получим с учетом ui-1 = Yi-1 0 1Xi-1: Yi=0(1)+Yi-1+1(Xi Xi-1) + i, где ошибка i удовлетворяет (4.11). Применяя обыкновенный МНК к последней модели, получаем оценку как коэффициента при Yi-1. б). Вычисляем значения преобразованных переменных и применяем к ним обыкновенный МНК. Получаем искомые оценки коэффициентов регрессии.Достоинством метода является простота его распространения на случай автокорреляции более высокого порядка. Как показывают эксперименты, проведенные для малых выборок, лучшим является двухшаговый метод 2, использующий оценку , полученную по методу, предложенному Дарбиным (метод 5 шаг а)). 4.5. Фиктивные переменные. Тест Чоу Факторы (объясняющие переменные), применяемые в задаче регрессии до сих пор, принимали значения из некоторого непрерывного интервала. Иногда может понадобиться ввести в модель переменные, значения которых детерминированы и дискретны. Например, данные получены для трех разных районов, или на двух фабриках, или на разных машинах и т.п. Переменные такого типа обычно называют фиктивными или искусственными. Эти переменные позволяют отразить в модели эффекты сдвига во времени или в пространстве, воздействия качественных переменных. Пример фиктивной переменной - это переменная X0 при свободном члене 0 в уравнении регрессии (3.1), которая принята равной 1. Эту переменную необязательно вводить в модель, но ее использование обеспечивает некоторое удобство в обозначениях. Во многих других случаях введение фиктивных переменных диктуется необходимостью. Пример. Допустим, мы хотим отразить в модели разное происхождение куриных окорочков (исходные данные7 - таблица 4.5), часть из которых получены в Америке, а часть в Канаде, при построении регрессионной зависимости веса окорочков Y от возраста кур X. Для этого в модель включим фиктивную переменную Z: Z=0 для Америки, Z=1 для Канады: Y=0 + 1X + Z. Таблица 4.5Данные для расчета модели с фиктивной переменной
Если бы мы построили регрессию Y на X, то получили бы такое уравнение Y=0,442+0,465X. Воспользовавшись моделью с фиктивной переменной получим Y=0,643+0,466X0,422Z или для различных стран: YK =0,221+0,466X для Канады и YA=0,643+0,466X для Америки. Экспериментальные данные и три прямые, подобранные методом наименьших квадратов, приведены на рис. 4.3. Все три линии практически параллельны. Дисперсионный анализ показывает значимость полученных зависимостей, причем уравнение (как с фиктивной переменной, так и без фиктивной переменной) объясняет до 80% вариации относительно среднего. Вывод, который можно сделать в этом случае введение фиктивной переменной не дает весомого улучшения модели в смысле дополнительно объясненной вариации. Ясно, что для какой-либо задачи существует не единственный способ выбора фиктивных переменных, а в большинстве случаев путей их представления много. Это обстоятельство оказывается выгодным, поскольку в некоторых случаях можно угодить в ловушку, когда существует линейная зависимость между введенными фиктивными переменными. Чтобы избежать ловушки, необходимо выбрать одну из категорий в качестве эталонной и определять фиктивные переменные для остальных возможных категорий, причем выбор эталонной категории не влияет на сущность регрессии. 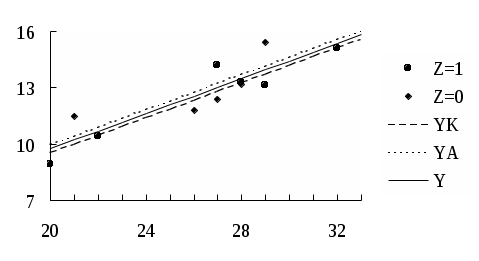 Рис. 4.3 Может потребоваться включение в модель более одной совокупности фиктивных переменных. Это особенно часто встречается при работе с перекрестными выборками. Поясним такую процедуру – множественных совокупностей фиктивных переменных – на примере8. Пример. Предположим, что исследуется зависимость между весом новорожденного и семейным положением матери, а также рожала ли она раньше. Введем фиктивную переменную M, которая принимает значения 1, если мать одинока, и 0 – в остальных случаях. Введем также фиктивную переменную числа родов в прошлом D, равную 1 для матерей, которые рожали в прошлом, и 0 для матерей, которые ранее не рожали. При этом двойном наборе фиктивных переменных имеется четыре возможных случая с соответствующими комбинациями значений фиктивных переменных: 1. Замужняя мать, первые роды M=0, D=0. 2. Одинокая мать, первые роды M=1, D=0. 3. Замужняя мать, не первые роды M=0, D=1. 4. Одинокая мать, не первые роды M=1, D=1. Первый случай по смыслу является основной совместной эталонной категорией. Коэффициент при M будет представлять оценку разности веса новорожденных, если мать одинока (ожидаем отрицательный знак коэффициента). Коэффициент при D будет представлять оценку дополнительного веса при рождении, если ребенок не является первенцем. Ребенок для четвертой категории матерей будет подвержен обоим воздействиям. Фиктивные переменные могут быть введены не только в правую часть регрессионного соотношения, но и зависимая переменная может быть представлена в такой форме. Это возможно в тех случаях, когда в качестве зависимой переменной мы рассматриваем ответы на вопросы, пользуется ли человек собственной машиной, имеет ли счет в банке и т.п., причем во всех случаях зависимая переменная принимает дискретные значения. Фиктивные переменные могут быть использованы для учета взаимодействия между различными группами факторов. Пример. Проиллюстрируем сказанное на примере с окорочками. Для построения двух прямых рассмотрим модель: Y=0+1X+Z(1+2X)+u или Y=0+1X+1Z+2XZ+u. Такой подход позволяет проверить различные варианты гипотез: 1. Гипотеза H0: 1=2=0 против альтернативы H1: что это не так. Если гипотеза H0 будет отвергнута, то мы придем к выводу, что модели не одинаковы, а если нет, то можно пользоваться одной моделью независимо от происхождения окороков. 2. Если гипотеза H0 в предыдущем пункте будет отвергнута, то можно проверить гипотезу H0: 2=0. Если H0 принимается, то мы заключаем, что имеющиеся два набора данных отличаются только уровнем, имея одинаковые углы наклона. При необходимости могут быть выбраны и другие варианты проверок, если это разумно для задачи. Получим для указанной выше модели уравнение МНК: Y=2,974+0,377X3,649Z+0,123(XZ), причем R2=0,82. Два отдельных уравнения для Z=1: Y=0,675+0,5X; и для Z=0: Y=2,974+0,377X. Как видно, уравнения несколько отличаются от тех линий, что приведены на рис. 4.3. Для проверки гипотезы H0: 1=2=0 составим таблицу дисперсионного анализа (табл. 4.6). Значение F=3,399/0,983=3,458, что меньше F0,05(2; 7)=4,74, а, следовательно, гипотеза H0 принимается, то есть можно пользоваться одной моделью как для окороков из Америки, так и из Канады. Последнее подтверждается ранее полученными результатами. Как показывает пример, использование взаимодействия с фиктивными переменными упрощает построение подходящих критериев и получение правильных статистик для проверки гипотез. Таблица 4.6
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
=167,41
=59,69