Курс лекций по дисциплине Эконометрика
 Скачать 2.09 Mb.
|
|
Значения элементов временного ряда формируются под воздействием ряда факторов, среди которых выделяют: долговременные, формирующие в длительной перспективе общую тенденцию анализируемого признака. Эта тенденция описывается с помощью некоторой функции, называемой трендом (Т); сезонные, формирующие периодически повторяемые в определенное время года колебания анализируемого признака (S); циклические, формирующие изменения анализируемого в результате воздействия циклов экономической, демографической или астрофизической природы (С); случайные, не поддающиеся учету и регистрации, как результат воздействия случайных, внешних факторов (U). Первые три составляющие часто объединяют в одну детерминированную и рассматривают модель ряда в виде yt=f(t)+ut, t. Изменение уровня f(t) со временем называют при этом трендом. Предметом анализа временного ряда является выделение и изучение указанных компонент ряда, как правило в рамках одной из моделей ряда: либо аддитивной Y=T+C+S+U, либо мультипликативной Y=TCSU. Некоторые составляющие могут отсутствовать в тех или иных рядах. В результате анализа временного ряда необходимо определить, какие из неслучайных составляющих присутствуют в разложении ряда, построить для них хорошие оценки, подобрать модель, описывающую поведение остатков и оценить ее параметры. 5.2. Проверка гипотезы о существовании тренда Для выявления факта наличия или отсутствия неслучайной составляющей f(t), то есть для проверки гипотезы о существовании тренда - Н0: Еy(t)=a=const, используют следующие критерии. I. Критерий серий. Упорядочим члены ряда по возрастанию: y1, y2, ..., yt, ..., yn. Определим медиану ряда: 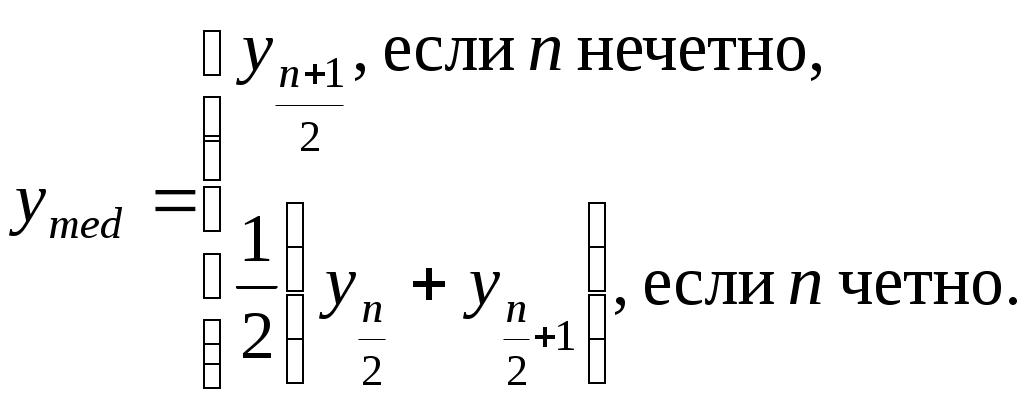 Образуем последовательность плюсов и минусов, соответствующую исходному ряду, по правилу: если yt>ymed, то yt соответствует плюс, если yt<ymed, то – минус. Под серией понимается последовательность подряд идущих плюсов и подряд идущих минусов. Подсчитаем общее число серий и протяженность самой длинной серии . Если хотя бы одно из неравенств:  окажется нарушенным, то гипотеза Н0 отвергается с вероятностью ошибки , заключенной между 0,05 и 0,0975. II. Критерий "восходящих" и "нисходящих" серий. Аналогично предыдущему критерию исследуется последовательность плюсов и минусов. Правило построения последовательности: если yt+1-yt>0, то yt соответствует плюс, если yt+1-yt<0, то – минус (если подряд идут несколько равных наблюдений, то во внимание принимается одно из них). Если хотя бы одно из неравенств: 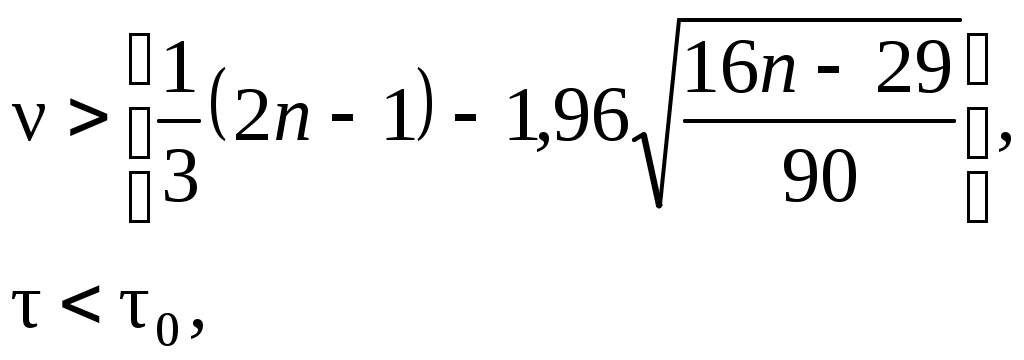 окажется нарушенным, то гипотеза Н0 отвергается с вероятностью ошибки , заключенной между 0,05 и 0,0975. Величина 0 определяется в зависимости от n:
III. Критерий квадратов последовательных разностей (критерий Аббе). Если есть основания полагать, что разброс наблюдений yt относительно своих средних значений подчиняется нормальному закону распределения вероятностей, то применяется критерий Аббе - см. [1], с. 801-802. 5.3. Аналитическое выравнивание временных рядов, оценка параметров уравнения тренда Метод обработки временных рядов, целями которого является устранение случайных колебаний и построение аналитической функции, характеризующей зависимость уровней ряда от времени – тренда, называется аналитическим выравниванием временного ряда. Суть метода аналитического выравнивания состоит в том, чтобы заменить фактические уровни временного ряда  на теоретические  . Расчет осуществляется по некоторому формализованному уравнению, принятому за математическую модель тренда. Для построения трендов чаще всего применяют такие функции, как:линейная:  ;степенная:  ;гиперболическая:  ;экспоненциальная:  ;полиномы второго и более высоких порядков:  .Расчет параметров тренда производится методом МНК. В качестве зависимой переменной выступают фактические уровни ряда , а независимой переменной является время  . Заметим, что для нелинейных трендов необходима процедура линеаризации, аналогичная рассмотренной в разделе 3.Выбор функции тренда может быть осуществлен несколькими способами. Наиболее простым считается тот, в ходе которого анализируют цепные абсолютные приросты (первые разности уровней ряда)  , абсолютные ускорения уровней ряда (вторые разности ряда)  и цепные коэффициенты роста . Если примерно одинаковы , то ряд имеет линейный тренд, если же примерно постоянны , то для описания тенденции временного ряда следует выбрать параболу второго порядка, и, если примерно равны , необходимо использовать экспоненциальную или степенную функции.Пример 1.9 Рассчитаем параметры уравнения тренда по следующим данным: Таблица 5.2 Темпы роста номинальной месячной заработной платы (за 10 месяцев 1999г., % к уровню декабря 1998г.)
Для выявления тенденции временного ряда рассчитаем цепные абсолютные приросты (первые разности уровней ряда) , абсолютные ускорения уровней ряда (вторые разности ряда) и цепные коэффициенты роста .Таблица 5.3
Наибольшей стабильностью отличаются цепные коэффициенты роста. Для описания тенденции временного ряда используем степенной или экспоненциальный тренд. Для того чтобы убедиться в этом, рассчитаем уравнение тренда и коэффициенты детерминации уравнения для наиболее часто применяемых функций, применяя МНК. Получим табл. 5.4. Коэффициенты детерминации рассчитаны по линеаризованным уравнениям регрессии. Как мы и предполагали, степенной тренд лучше всего описывает тенденцию анализируемого временного ряда, что подтверждается высоким значением коэффициента детерминации. Таблица 5.4 Уравнения трендов
Интерпретация параметров тренда существенно зависит от его типа. Если тренд имеет линейную форму, то a- начальный уровень временного ряда в период времени t=0 и b- средний за период абсолютный прирост уровней ряда. Если же ряд имеет, например, экспоненциальный тренд, то a - начальный уровень временного ряда в период времени t=0 и  - средний за единицу времени коэффициент роста уровней ряда. Трактовка параметров степенного тренда аналогична трактовке параметров экспоненциального тренда. Пример (продолжение примера 1). Согласно уравнению линейного тренда  темпы роста заработной платы за 10 месяцев 1999 г. изменялись от начального уровня 82,66% со средним за месяц абсолютным приростом в 4,72 процентных пункта. Мы можем заменить фактические уровни временного ряда  на теоретические  , подставляя значения tв уравнение тренда: Уравнение экспоненциального тренда в исходной форме имеет вид:  Таким образом, начальный уровень ряда в начальный период времени равен 83,96, а средний цепной коэффициент роста - 1,045. Следовательно, темпы роста заработной платы за 10 месяцев 1999 г. изменялись от начального уровня 83,96% со средним за месяц цепным коэффициентом роста в 104,5%. Теоретические значения временного ряда рассчитываются как:  Уравнение тренда параболы второго порядка имеет вид:  .Следовательно, темпы роста заработной платы за 10 месяцев 1999 г. изменялись от начального уровня 72,9% со среднемесячным абсолютным приростом, описываемым зависимостью вида  . Теоретические значения уровней ряда могут быть рассчитаны как: |
