Курс лекций по дисциплине Эконометрика
 Скачать 2.09 Mb.
|
|
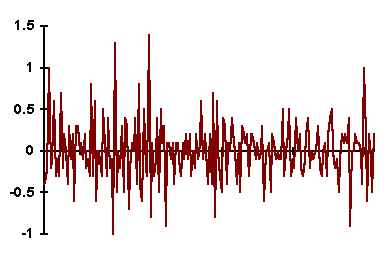
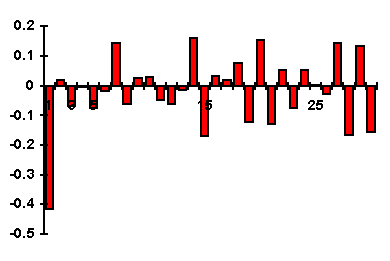
5.6. Модели стационарных и нестационарных временных рядов и их идентификация Модели авторегрессии порядка p (AutoRegressive - AR(p) models). Достаточно часто экономические показатели, представленные в виде временного ряда, имеют сложную структуру. Моделирование таких рядов путем построения модели тренда, сезонности и периодической составляющей не приводит к удовлетворительным результатам. Ряд остатков часто имеет статистические закономерности. Наиболее распространенными моделями стационарных рядов являются модели авторегрессии и модели скользящего среднего. Будем рассматривать класс стационарных временных рядов. Задача состоит в построении модели остатков временного ряда ut и прогнозирования его значений. Авторегрессионная модель предназначена для описания стационарных временных рядов. Стационарный процесс удовлетворяет уравнению авторегрессии бесконечного порядка с достаточно быстро убывающими коэффициентами. В частности поэтому авторегрессионная модель достаточно высокого порядка может хорошо аппроксимировать почти любой стационарный процесс. В связи с этим модель авторегрессии часто применяется для моделирования остатков в той или иной параметрической модели, например регрессионной модели или модели тренда. Модель авторегрессии порядка 1AR(1) (марковский процесс). Марковскими называются процессы, в которых состояние объекта в каждый следующий момент времени определяется только состоянием в настоящий момент и не зависит от того, каким путем объект достиг этого состояния. В терминах корреляционного анализа для временных рядов марковский процесс можно описать следующим образом: существует статистически значимая корреляционная связь исходного ряда с рядом, сдвинутым на один временной интервал, и отсутствует с рядами, сдвинутыми на два, три и т. д. временных интервала. В идеальном случае эти коэффициенты корреляции равны нулю. Авторегрессионная модель первого порядка определяется соотношением: u(t)= u(t-1)+(t) , (5.1) где - числовой коэффициент <1, (t) – последовательность случайных величин, образующих «белый шум» (E((t))=0, E((t)(t+))= 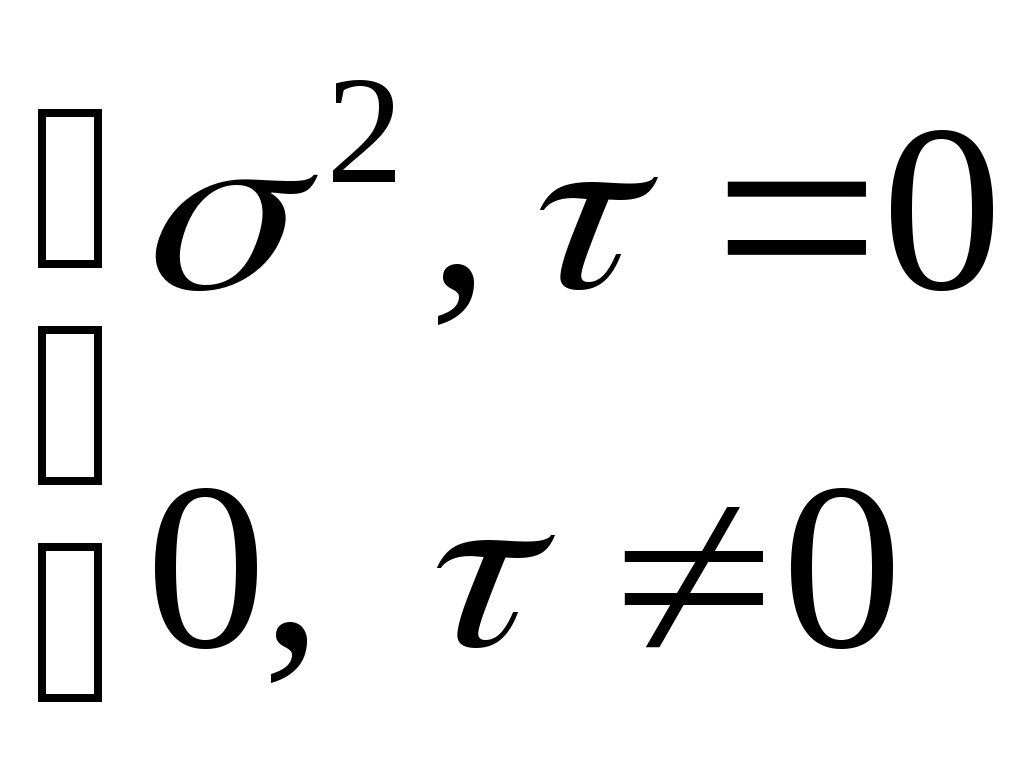 ). Модель (5.1) называется также марковским процессом. Имеем: E(u(t))0. (5.2) r(u(t)u(t))=. (5.3) Du(t)=2/(1-2). (5.4) cov(u(t)u(t))=Du(t). (5.5) Из (5.3) следует, что при близком к единице дисперсия u(t) будет намного больше дисперсии t. Это значит (учитывая (5.2) =r(u(t)u(t1))=r(1), т.е. параметр может быть интерпретирован как значение автокорреляции первого порядка), что в случае сильной корреляции соседних значений ряда u(t) ряд слабых возмущений t будет порождать размашистые колебания остатков u(t). Условие стационарности ряда (5.1) определяется требованием <1. Автокорреляционная функция (АКФ) r() марковского процесса определяется соотношением (5.3). Частная автокорреляционная функция rчаст()=r(u(t)u(t+)) u(t+1)=u(t+2)=…=u(t+-1)=0 может быть вычислена по формуле: rчаст(2)=(r(2)-r2(1))/(1-r2(1)). Для второго и выше порядков (см. [1], с. 413, 414) должно быть rчаст()=0 =2,3,… . Это удобно использовать для подбора модели (5.1): если вычисленные по оцененным невязкам u(t)=yt-  выборочные частные корреляции статистически незначимо отличаются от нуля при=2,3,…, то использование модели AR(1) для описания случайных остатков не противоречит исходным данным. Идентификация модели. Требуется статистически оценить параметры и 2 модели (5.1) по имеющимся значениям исходного ряда yt. Выделяем неслучайную составляющую 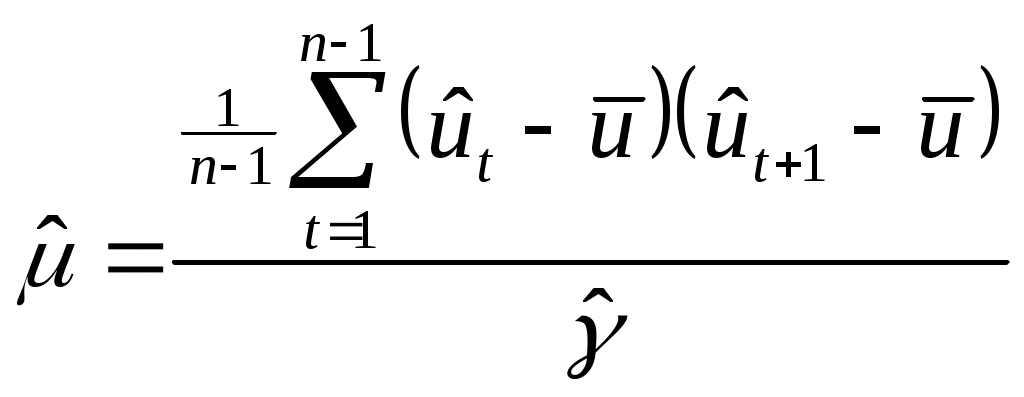и получаем невязки  . Находим дисперсию невязок  , где  (для большинства методов выделения автоматически  =0). Далее с учетом (5.2), (5.3) получим формулы для оценки параметров модели (5.1): , .Модели авторегрессии р порядка – AR(p) при p2 см. в [1], с. 834-837: u(t)=1u(t-1)+2u(t-2)+…+(t). (5.6) Пример. График первой разности ряда, хорошо описывающейся моделью AR(1), представлен на рис. 5.1; график выборочной автокорреляционной функции (АКФ) первой разности этого ряда представлен на рис. 5.2.
|
