Курс лекций по дисциплине Эконометрика
 Скачать 2.09 Mb. Скачать 2.09 Mb.
|
2.4. Коэффициент корреляции, коэффициент детерминации, корреляционное отношениеДля трактовки линейной связи между двумя переменными акцентируют внимание на коэффициенте корреляции. Пусть имеется выборка наблюдений (Xi, Yi), i=1,...,n, которая представлена на диаграмме рассеяния, именуемой также полем корреляции (рис. 2.3). Y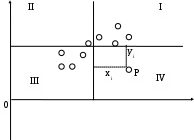 X Рис. 2.3. Диаграмма рассеяния Разобьем диаграмму на четыре квадранта так, что для любой точки P(Xi, Yi) будут определены отклонения Ясно, что для всех точек I квадранта xiyi>0; для всех точек II квадранта xiyi<0; для всех точек III квадранта xiyi>0; для всех точек IV квадранта xiyi<0. Следовательно, величина xiyi может служить мерой зависимости между переменными X и Y. Если большая часть точек лежит в первом и третьем квадрантах, то xiyi>0 и зависимость положительная, если большая часть точек лежит во втором и четвертом квадрантах, то xiyi<0 и зависимость отрицательная. Наконец, если точки рассеиваются по всем четырем квадрантам xiyi близка к нулю и между X и Y связи нет. Указанная мера зависимости изменяется при выборе единиц измерения переменных X и Y. Выразив xiyi в единицах среднеквадратических отклонений, получим после усреднения выборочный коэффициент корреляции: 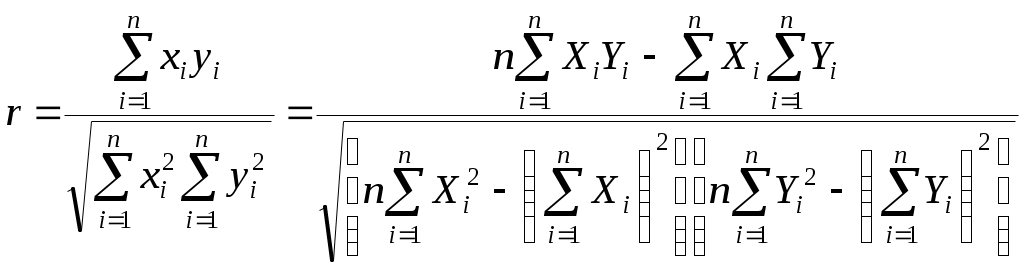 (2.9) (2.9)Из последнего выражения можно после преобразований получить следующую формулу для квадрата коэффициента корреляции: 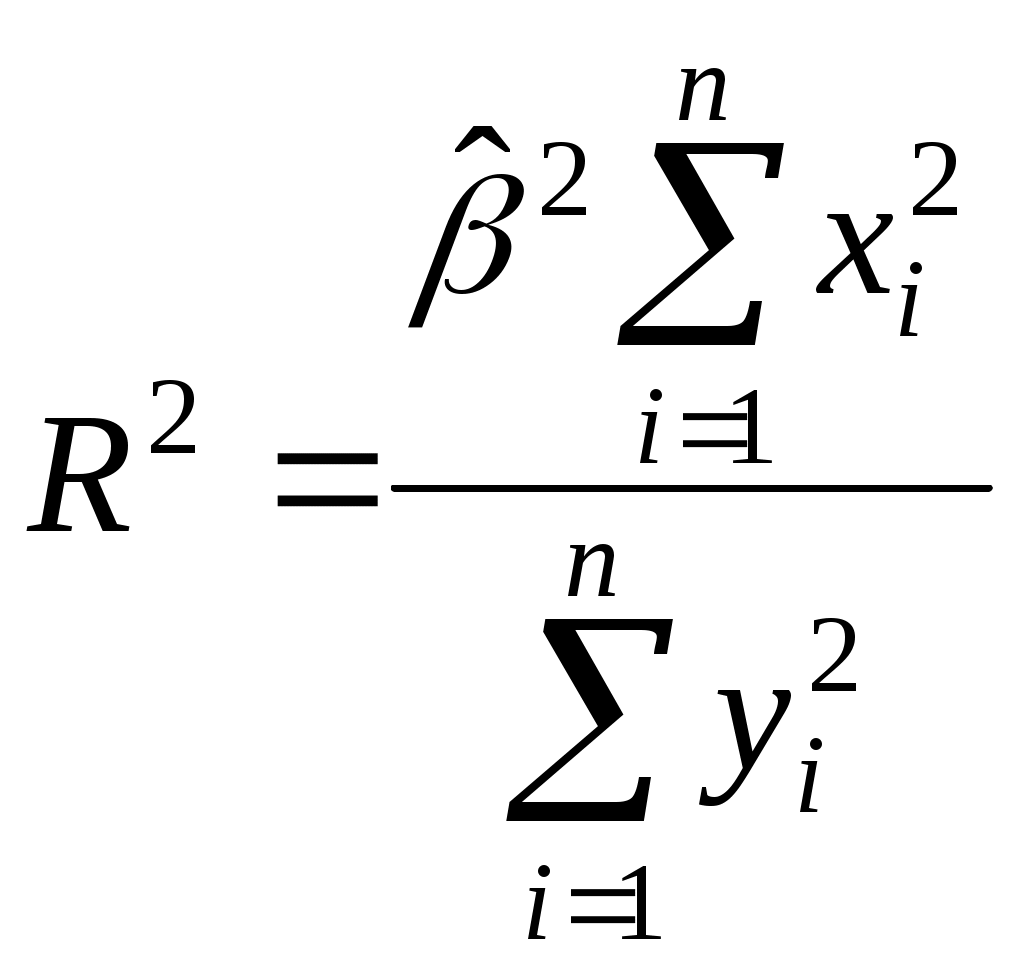 или или 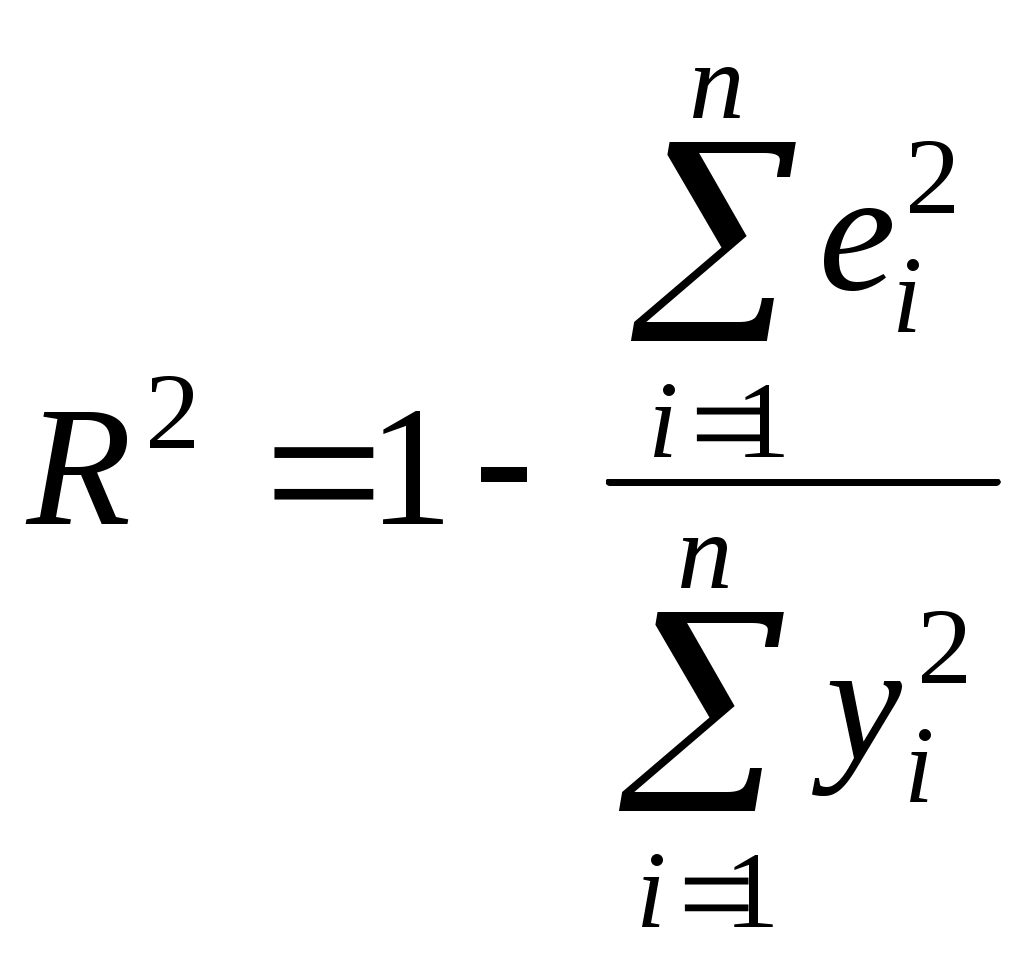 (2.10) (2.10)Квадрат коэффициента корреляции называется коэффициентом детерминации. Согласно (2.10) значение коэффициента детерминации не может быть больше единицы, причем это максимальное значение будет достигнуто при Кроме того, из (2.10) следует, что коэффициент детерминации равен доле дисперсии Y (знаменатель формулы), объясненной линейной зависимостью от X (числитель формулы). Это обстоятельство позволяет использовать R2 как обобщенную меру "качества" статистического подбора модели (2.6). Чем лучше регрессия соответствует наблюдениям, тем меньше Поскольку коэффициент корреляции симметричен относительно X и Y, то есть rXY=rYX, то можно говорить о корреляции как о мере взаимозависимости переменных. Однако из того, что значения этого коэффициента близки по модулю к единице, нельзя сделать ни один из следующих выводов: Y является причиной X; X является причиной Y; X и Y совместно зависят от какой-то третьей переменной. Величина r ничего не говорит о причинно-следственных связях. Эти вопросы должны решаться, исходя из содержательного анализа задачи. Следует избегать и так называемых ложных корреляций, т.е. нельзя пытаться связать явления, между которыми отсутствуют реальные причинно-следственные связи. Например, корреляция между успехами местной футбольной команды и индексом Доу-Джонса. Классическим является пример ложной корреляции, приведенный в начале ХХ века известным российским статистиком А.А. Чупровым: если в качестве независимой переменной взять число пожарных команд в городе, а в качестве зависимой переменной – сумму убытков от пожаров за год, то между ними есть прямая корреляционная зависимость, т.е. чем больше пожарных команд, тем больше сумма убытков. На самом деле здесь нет причинно-следственной связи, а есть лишь следствия общей причины – величины города. Проверка гипотезы о значимости выборочного коэффициента корреляции эквивалентна проверке гипотезы о =0 (см. ниже) и, следовательно, равносильна проверке основной гипотезы об отсутствии линейной связи между Y и X. Вычисляя значение t-статистики вывод о значимости r делается при t>t, где t - соответствующее табличное значение t-распределения с (n-2) степенями свободы и уровнем значимости . Пример. Вычислим коэффициент корреляции и проверим его значимость для нашего примера табл. 2.1. По (2.9) r=43145/(4651040068,25)0,5=0,9994. R2=0,998. Значение t-статистики t=0,9994[10/(1-0,998)]0,5=70,67. Поскольку t0,05;10=2,228, то t>t0,05;10 и коэффициент корреляции значим. Следовательно, можно считать, что линейная связь между переменными Y и X в примере существует. Если между переменными имеет место нелинейная зависимость, то коэффициент корреляции теряет смысл как характеристика степени тесноты связи. В этом случае используется наряду с расчетом коэффициента детерминации расчет корреляционного отношения. Предположим, что выборочные данные могут быть сгруппированы по оси объясняющей переменной X. Обозначим s – число интервалов группирования, 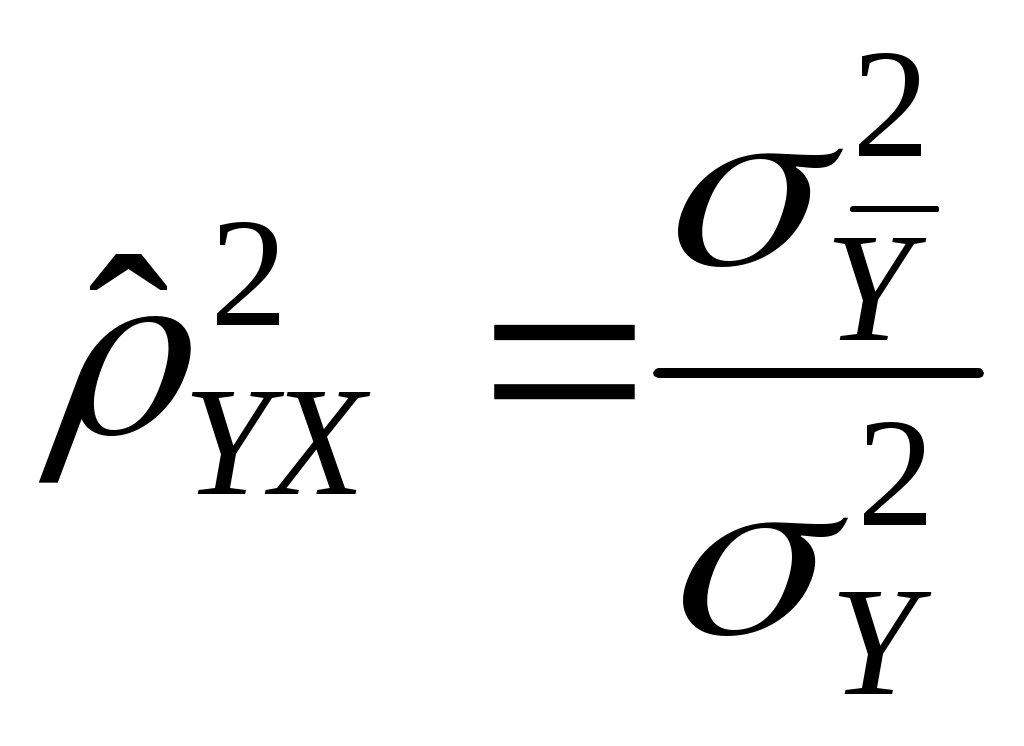 . (2.11) . (2.11)Величину Величина Можно показать, что Это позволяет использовать величину разности 2.5. Оценка статистической значимости регрессии Перейдем к вопросу о том, как отличить "хорошие" оценки МНК от "плохих". Конечно, предполагается, что существуют критерии качества рассчитанной линии регрессии. Перечислим способы, которые помогают решить вопрос о достоинствах рассчитанной линии регрессии: построение доверительных интервалов и оценка статистической значимости коэффициентов регрессии по t-критерию Стьюдента; дисперсионный анализ и F – критерий Фишера; проверка существенности выборочного коэффициента корреляции (детерминации). Перейдем к подробному изложению свойств оценок МНК и способов проверки их значимости. Несложно показать, что оценки Для вычисления интервальных оценок , предполагаем нормальное распределение случайной величины u. Для получения интервальных оценок , оценим дисперсию случайного члена 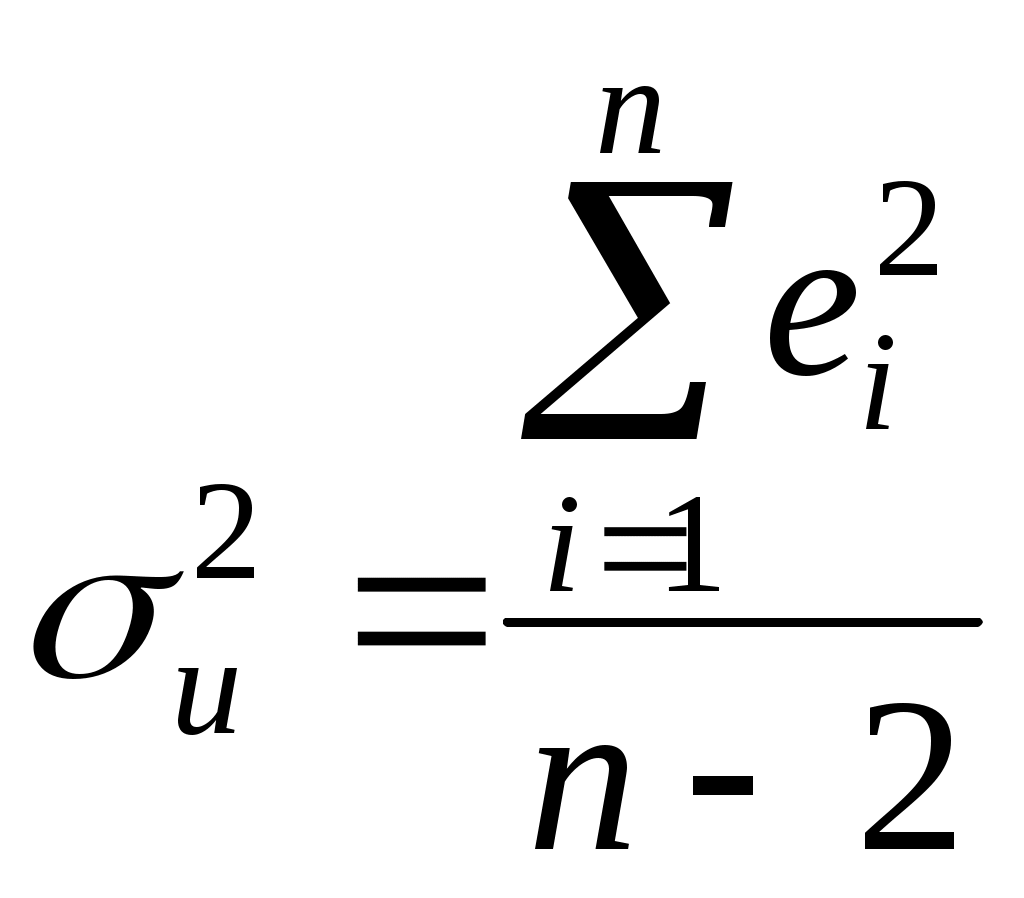 . (2.12) . (2.12)Вычислим величину 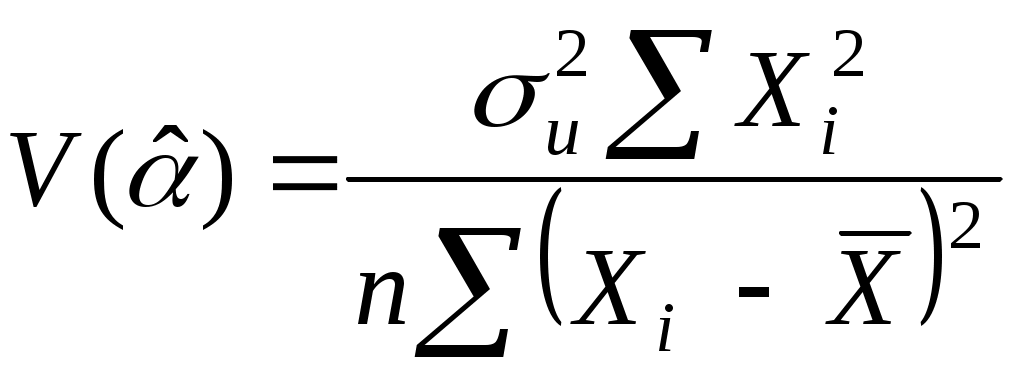 , ,и Статистика имеет t-распределение Стьюдента. Так как 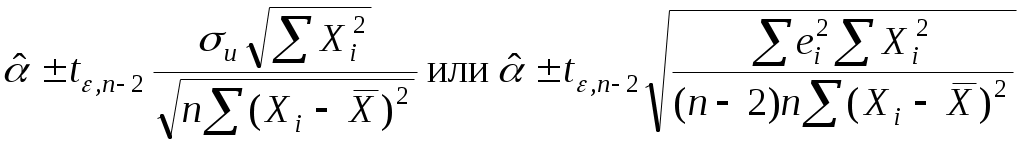 , (2.13) , (2.13)где t,n-2 – табличное значение t распределения для (n-2) степеней свободы и уровня значимости . Вычислим величину 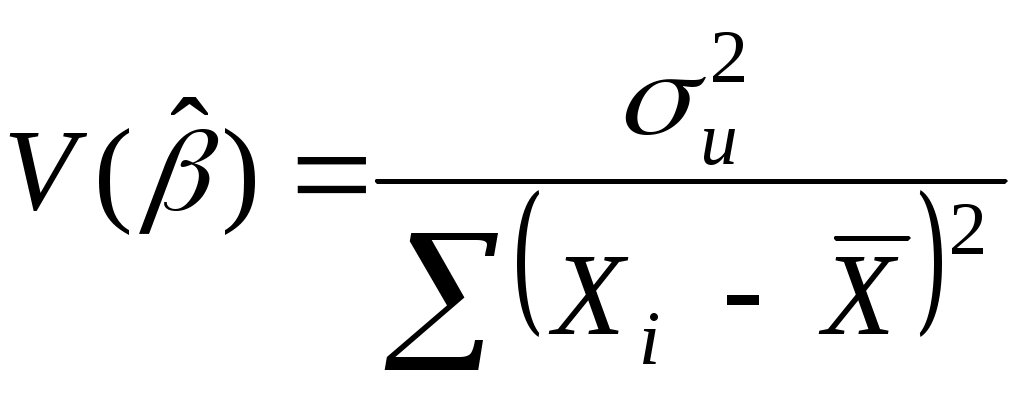 , ,и Статистика имеет t-распределение Стьюдента. Так как 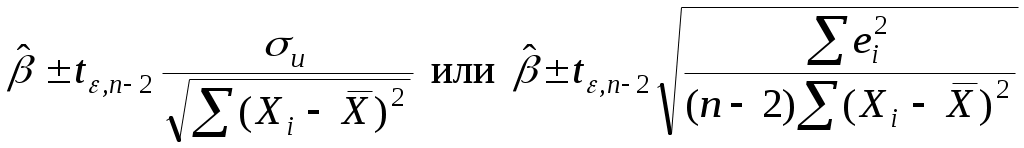 , (2.14) , (2.14)где t,n-2 – табличное значение t распределения для (n-2) степеней свободы и уровня значимости . Проверим гипотезу о равенстве нулю коэффициента , т.е. H0: =0. С учетом статистики 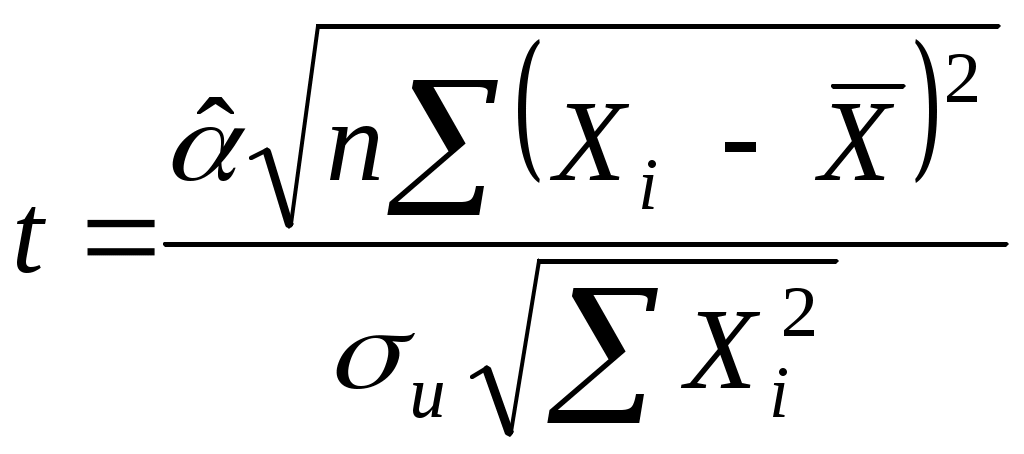 . (2.15) . (2.15)Если вычисленное по (2.15) значение t будет больше t для заданного критического уровня значимости , то гипотеза H0 о равенстве нулю коэффициента отклоняется, если же t<t, то H0 принимается. Аналогично для проверки гипотезы о равенстве нулю коэффициента , т.е. H0: =0 рассчитаем статистику: 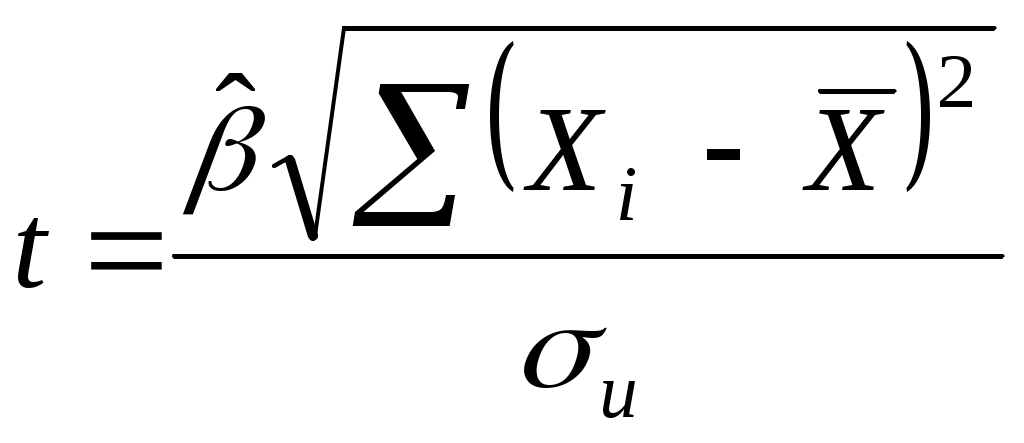 . (2.16) . (2.16)Если вычисленное по (2.16) значение t будет больше t для заданного критического уровня значимости , то гипотеза H0 о равенстве нулю коэффициента отклоняется, если же t<t, то H0 принимается. Заметим, что формула (2.12) может быть упрощена и записана в виде: Пример. Приведем расчеты для нашего примера в табл. 2.1. По формуле (2.17) рассчитаем дисперсию ошибки: Найдем доверительный интервал для по первой из формул (2.13): = По таблице t-распределения находим t0,05;10=2,228 и =-2,912,2282668,219/747,0743. Откуда =-2,917,798 или -10,74,9. С вероятностью 0,95 истинные значения находятся в интервале 10,74,9. Аналогично найдем доверительный интервал для по первой из формул (2.14): = Кроме того по экономическому смыслу переменных примера следует ожидать, что 01. Поскольку доверительный интервал не включает 0 и 1, то результаты регрессии соответствуют гипотезе 01. Проверим гипотезу о равенстве нулю коэффициента , т.е. H0: =0. Рассчитаем t-статистику по формуле (2.16): t=0,9276 Табличное значение t0,01;10=3,169, так как t>t0,01;10, то гипотеза о том, что =0 отклоняется. Можно говорить о том, что коэффициент значимо отличен от нуля. Разложим общую вариацию значений Y около их выборочного среднего Сумма квадратов отклонений от среднего в выборке равна сумме квадратов отклонений значений Первую связывают с линейным воздействием изменений переменной X и называют "объясненной". Вторая составляющая является остатком и называется "необъясненной" долей вариации переменной Y. Отметим, что долю дисперсии, объясняемую регрессией, в общей дисперсии результативной переменной Y характеризует коэффициент детерминации, определяемый по формуле (2.10), которая может быть преобразована с учетом (2.18) к виду: Предположим, что мы хотим проверить гипотезу об отсутствии линейной функциональной связи между X и Y, т.е. H0: =0. Иначе говоря, мы хотим оценить значимость уравнения регрессии (2.6) в целом. Для проверки гипотезы сведем необходимые вычисления в таблицу (табл. 2.3). Соотношение удовлетворяет F - распределению Фишера с (1, n-2) степенями свободы. Критические значения этой статистики F для уровня значимости затабулированы. Если F>F, то гипотеза об отсутствии связи между переменными Y и X отклоняется, в противном случае гипотеза Н0 принимается и уравнение регрессии не значимо. Таблица 2.3 Таблица дисперсионного анализа
Пример. Для примера табл. 2.1, с учетом предыдущих вычислений, будем иметь таблицу анализа дисперсии - табл. 2.4. Применяя формулу (2.19), получим 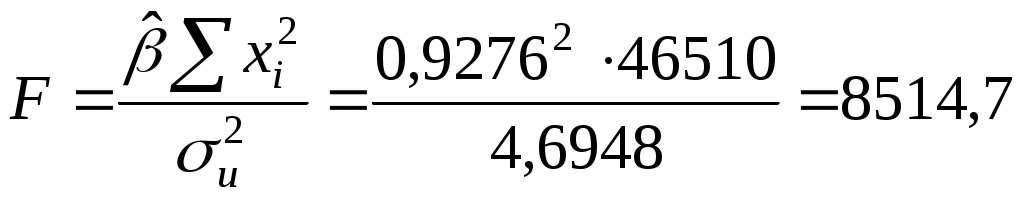 . Табличное значение F0,01(1, 10)=10,04, так что имеющиеся данные позволяют отвергнуть гипотезу об отсутствии связи между личными доходами и индивидуальным потреблением. . Табличное значение F0,01(1, 10)=10,04, так что имеющиеся данные позволяют отвергнуть гипотезу об отсутствии связи между личными доходами и индивидуальным потреблением. Таблица 2.4 Таблица анализа дисперсии (пример в табл. 2.1)
2.6. Интерпретация уравнения регрессии Проанализируем, какую информацию дает нам оцененное уравнение регрессии (2.6), т.е. поставим вопрос об интерпретации (содержательном объяснении) коэффициентов уравнения. Во-первых, можно сказать, что увеличение X на одну единицу (в единицах измерения переменной X) приведет к увеличению/уменьшению (в зависимости от знака коэффициента Во-вторых, необходимо проверить, в каких единицах измерены переменные X и Y и можно ли заменить слово "единица" фактическим количеством (рубли, тонны и т.п.). В-третьих, константа Часто рассчитывают средний коэффициент эластичности Пример. Продолжая рассмотрение примера п. 2.1, проинтерпретируем уравнение регрессии между индивидуальным потреблением и личными доходами в США: Поскольку обе переменные измерены в $, то интерпретация облегчается. Смысл коэффициента Константа в данном случае не имеет никакого смысла применительно к совокупности, поскольку мы не можем сказать, что при нулевых доходах потребление граждан США составит -2,91 млрд. долларов. Рассчитаем средний коэффициент эластичности: Т.е. при изменении личных доходов на 1% от своего среднего значения в среднем по совокупности индивидуальное потребление изменится на 0,923% от своей средней величины. При интерпретации уравнения регрессии важно помнить о следующих фактах: величины уравнение регрессии отражает общую тенденцию для выборки, а каждое отдельное наблюдение при этом подвержено воздействию случайностей; верность интерпретации зависит от правильности спецификации уравнения, то есть включения/исключения соответствующих объясняющих переменных и выбора вида функции регрессии. |
