Курс лекций по биомеханике. Курс лекций Содержание Биомеханика как учебная и научная

• Название: Курс лекций Содержание Биомеханика как учебная и научная
• Анкор: Курс лекций по биомеханике.doc
• Дата: 24.04.2017
• Размер: 5.94 Mb.
• Имя файла: Курс лекций по биомеханике.doc
• Тип: Курс лекций; #1886
• страница: 7 из 26

Тема 5. КИНЕМАТИЧЕСКИЕ ХАРАКТЕРИСТИКИ ДВИЖЕНИЙ ЧЕЛОВЕКА

1. Системы отсчета расстояния и времени 2. Пространственные характеристики 3. Временные характеристики 4. Пространственно-временные характеристики 5. Кинематические особенности движений человека.

1. СИСТЕМЫ ОТСЧЕТА РАССТОЯНИЯ И ВРЕМЕНИ

Движение физического объекта обнаруживается только в сопостав­лении положений объекта с положением другого тела (тела отсчета), т. е. как относительное.

1.1. Выбор тела отсчета

Телом отсчета называют условно выбранное тело, от которого отсчитывают расстояние при определении изучаемого относитель­ного движения.

Движение выражается в изменении с течением времени взаимного положения тел. Его можно наблюдать и отсчитывать только относи­тельно других реальных тел (например, при прыжке в длину—отно­сительно бруска) или условных (например, в старте яхт — относительно линии створа).

В зависимости от условий задачи выбирается та или иная система отсчета. При отсчете расстояний надо установить: а) начало, б) направление и в) единицы отсчета. Систему от­счета связывают с определенным физическим телом отсчета. Очень важно целесообразно выбрать тело и начало отсчета.

На отсчет расстояний в изучаемом движении совершенно не влияло бы движение тела отсчета без ускорения; но тел, движущихся без уско­рения, в природе просто не существует. Условно принято считать «неподвижным», неускоряемым (и н е р ц и а л ь н ы м) телом от­счета такое тело, ускорение которого столь мало, что не сказывается заметно па отсчете данного наблюдаемого движения.

Например, годовое и суточное движение Земли незаметно при отсчете движений в спортивной практике, хотя скорости движений Земли значительны: скорость точки, находящейся, например, на широте Москвы, при суточном вращении Земли вокруг оси равна 0,261 км/сек, а при годовом вращении по ее орбите вокруг Солнца — 30 км/сек. Землю и неизменно связанные с нею тела (например, спортивные соору­жения) и выбирают как практически инерциальные тела отсчета.

Иногда целесообразен или просто неизбежен выбор «подвижных», т. е. ускоряемых, тел отсчета (неинерциальных). Они дви­жутся с такими ускорениями, которые существенно влияют на отсчет движения. Например, определяя, каковы особенности движений ног в тазобедренных суставах у гимнаста при махе на кольцах, можно вести отсчет относительно таза, который сам тоже движется.

От выбора тела отсчета зависят многие характеристики изучаемого движения. Характер движения всех инерциальных тел отсчета, нахо­дящихся в относительном покое или прямолинейном и равномерном движении, не влияет на изучаемые характеристики, тогда как характер движения неинерциальных тел отсчета влияет на них, причем по-раз­ному в зависимости от ускорений.

Само тело отсчета условно рассматривается как абсолютно твердое, т. е. не изменяющее своей формы при любых воздействиях.

1.2. Начало и направление отсчета расстояния

На теле отсчета устанавливают начало и направление измерения расстояния.

Физические тела, в том числе и тело человека, в некоторых случаях можно рассматривать как материальные точки.

Это возможно, если расстояние, на которое они передвигаются, несравнимо больше их собственных размеров и если можно пренебречь вращательным движением тела (например, при полете диска по траектории). Для точного определения спортив­ного результата правила соревнований строго предусматривают, по какой точке (пункт отсчета) ведется отсчет (по уровню лыжных креплений, по выступающей точке грудной клетки спринтера, по заднему краю следа приземляющегося прыгуна . и т. п.).

Итак, либо все движущееся тело рассматривают как материальную точку, до которой измеряют расстояние, либо на нем выделяют пункты отсчета. Расстояние измеряется от начала отсчета до пункта отсчета. В качестве такого пункта выбирается определенная точка движущегося тела человека. В случае вращательного движения выбирают линию отсчета.

Существует три основных способа определения движения точки: естественный, координатный и векторный.

При естественном способе заранее известна траектория точки; на ней следует выбрать начало (о) отсчета (например, контрольный пункт на трассе дистанции). Тогда положение точки (например, гон­щика) на траектории определяется расстоянием ее от начала отсчета (естественная координата). Надо еще указать, с какой стороны от на­чала отсчета (знаком + или —) расположена на траектории точка (рис. 17, а). Положение точки на линии определяется всего одним чис­лом со знаком + или —.

Координатный способ позволяет определить положение точки в ко­ординатах на плоскости и в пространстве. Чаще применяют прямоугольные координаты.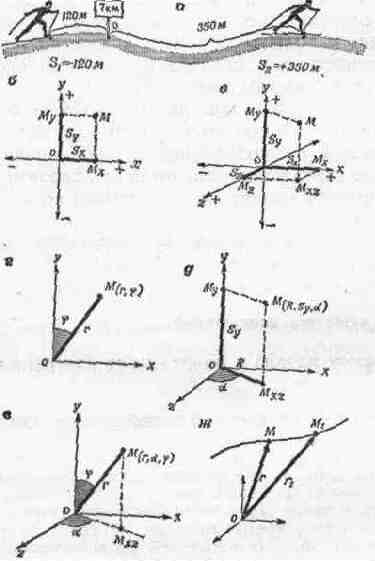



Рис. 17, Способы отсчета движения точки:

а — естественный способ; бвгде — координатный способ: и — на плоскости, в — в пространстве, г — полярные, д — цилиндрические, е — сфериче­ские; ж — векторный способ (ориг.)

Расстояние от начала коор­динат до проекции точки на все три оси (Мх, Му, А1,)— это три линейные коор­динаты: абсцисса, ордината и аппликата , полностью определяющие по­ложение точки в простран­стве. Можно пользоваться также и угловыми ко­ординатами: на плоско­сти — в системе полярных координат (см. рис. 17, г), а в пространстве — в системах цилиндри­ческих (см. рис. 17, д) и сферических координат (см. рис. 17, е).

Векторный способ сводится к установлению расстояния точки от начала отсчета, а также направления радиуса-вектора (рис. 17, ж)¹.

1.3. Единицы отсчета расстояния

В зависимости от выбранного способа отсчета устанавливаются единицы отсчета расстояния — линейные и угловые.

Линейные единицы. Чаще всего используют метрические единицы: основная — метр, кратная ей — километр (1000 м) и дольные—сантиметр (0,01 м) и миллиметр (0,001 м).

Кроме этой удобной для вычислений системы с десятичной зависимостью между меньшими и большими единицами пока все еще сохраняется в некоторых странах (встречается, в частности, и в спорте) очень неудобная для расчетов система:

1 дюйм=2,54 см; 1 фут==30,48 см; 1 ярд=91,44 см;

1 ярд=3 фута=36 дюймов;

1 м= 1.094 ярда=3,28 фута==39,4 дюйма.

Угловые единицы. В биомеханике применяются: а) градусы, ми­нуты, секунды — при непосредственном измерении углов (окружность=-360°; градус=60'; минута=60"); б) обороты—при прибли­женном определении поворотов (оборот=360°, пол-оборота== 180°, четверть оборота==90° и т. д.); в) радиан—для расчетов по форму­лам — угол между двумя радиусами круга, вырезающими на окруж­ности дугу, по длине равную радиусу (радиан=57° 17'44,8"; 1°=0,01745рад.).

1.4. Начало и единицы отсчета времени

Кроме протяженности движения (в пространстве) необходимо изме­рять его длительность (во времени). В обычных условиях жизни в сут­ках приняты два начала отсчета времени (полночь и полдень), на тран­спорте и в технике связи — одно (астрономическое — полночь). В спор­тивных соревнованиях, естественно, существует одно общее начало отсчета — это либо астрономическое время, либо судейское («секундо­меры на ноль»). В биомеханике в качестве начала отсчета времени вы­бирается момент начала изучаемого движения.

Единица отсчета времени — секунда (составляет 1/60 минуты, или 1/.3600 часа). В современном спорте учитываются еще деся­тые и сотые доли секунды, а в биомеханических исследованиях также и тысячные. Течение времени, естественно, рассматривается от прошлого к будущему, но при анализе движений иногда целесообразно вести отсчет также и в обратную сторону.

2. ПРОСТРАНСТВЕННЫЕ ХАРАКТЕРИСТИКИ

Пространственные характеристики в целом определяют простран­ственную форму движений человека.

2.1. Координаты точки, тела и системы

Координата — это пространственная мера местоположения точки относительно системы отсчета. Местоположение точки обычно определяют по ее линейным координатам:

. Координаты показывают, где находится изучаемая точка (например, пункт отсчета на теле) относительно начала отсчета, на каком расстоянии и в каком направ­лении от него. Для определения положения одной точки на линии необходимо и достаточно одной координаты, положения одной точки на поверхности—двух, в пространстве—трех.

Но, чтобы определить положение какого-либо твердого тела в про­странстве, этого недостаточно. Надо еще знать координаты углового положения тела (угловые координаты), определяющие его ориента­цию относительно этих трех осей:

Еще сложнее определение положения многозвенной биомехани­ческой системы (тела человека), изменяющей свою конфигурацию¹. Здесь уже нужно знать положение каждого звена в пространстве. Часто определяют положение тела по положениям проекций осей суставов на его поверхности (пунктов отсчета).

Различают исходное и конечное положения, т. е. положение, из которого движение начинается, и положение, которым оно заканчивается. От исходного положения (например, стартового) часто зависят многие особенности последующего движения. Конечное положение, к которому надо прийти, также может сильно влиять на выполнение движения (приземление после соскока со снаряда в гим­настике, после прыжка в длину в легкой атлетике, после выпуска снаряда в метаниях). Иногда исходное положение не очень сущест­венно (перед началом разбега при прыжке в высоту); в некоторых случаях и конечное почти безразлично (после передачи мяча в фут­боле).

Все движения можно представить себе как сплошной ряд мгновенных (непрерывно сменяющихся) промежуточных по­ложений. Так выглядит движение на кадрах кинопленки. По этим положениям можно приближенно восстановить внешнюю кар­тину выполнения движения. С точки зрения механики описать движение точки — значит определить ее поло­жение в любой момент времени.

2.2. Перемещение точки, тела и системы

Перемещение точки — это пространственная мера изменения местоположения точки в данной системе отсчета. Перемещение (линейное) измеряется разностью координат в моменты начала и окончания движения в одной и той же системе отсчета расстоя­ний:

Линейное перемещение точки показывает, на каком расстоянии в результате движения оказалась точка относительно начального (исходного) положения. Перемещение — величина векторная. Она характеризуется численным значением (модулем) и направ­лением, т. е. определяет раз­мах и направление движения. Если после движения точка вернулась в исходное поло­жение, перемещение равно нулю. Таким образом, пере­мещение есть не само движе­ние, а лишь его окончательный результат — расстояние по прямой и направление от исходного до конечного поло­жения.

Перемещение тела изме­ряется различно в случаях поступательного и вращатель­ного движений.

При поступатель­ном движении любая прямая, соединяющая какие-либо две точки тела, все время остается параллельной самой себе, при этом все точки тела движутся одинаково, скорости их равны. Следовательно, перемещение тела при поступательном движении можно определить по перемещению любой его точки. Для этого из каждой коор­динаты конечного положения точки надо вы­честь соответствующую координату началь­ного положения.

При вращательном движении какие-либо две точки, неизменно связанные с ним (внутри или вне тела), остаются во время всего движения неподвижными¹, при этом все точки тела, кроме неподвижных, движутся по дугам ок­ружностей, центры которых лежат на одной неподвижной линии — оси вращения, линей­ные скорости точек тела пропорциональны их расстояниям от оси. Следовательно, перемещение тела при вращательном движении можно измерить углом поворота — разностью угловых координат в одной и той же системе отсчета расстояний:

Любое движение тела в пространстве можно представить как гео­метрическую сумму поступательного и вращательного (вокруг центра тяжести) движений ².

Намного сложнее определить перемещение биомеханической системы,изменяющей свою конфигурацию. В самых упрощенных случаях дви­жение биомеханической системы рассматривают как движение одной материальной точки — обычно его общего центра тяжести (ОЦТ). Тогда можно проследить за перемещением всего тела человека «в це­лом», оценить в известной мере общий результат его двигательной дея­тельности. Но остается неизвестным, в результате каких именно движений достигнуто перемещение ОЦТ. Иногда перемещение тела представляют в виде перемещения условно связанной с ним линии (линия отсчета). Достоинства и недостатки этого способа в основном те же, что и в предыдущем.

Изучение у человека движений звеньев позволяет более подробно рассмотреть перемещение его тела. В некоторых случаях подвижные части (например, все кости стопы, кисти, предплечья, даже туловища) рассматриваются как одно звено. Здесь уже можно в общих чертах уловить особенности движений, хотя взаимное движение многих звеньев не учитывается и их деформациями пренебрегают. Однако получить полную картину перемещений всех существенных элементов тела (включая и внутренние органы, и жидкие ткани) при существую­щих методах исследования пока еще невозможно. Всегда приходится прибегать к более или менее значительному упрощению, которое неиз­бежно вообще в любом научном исследовании.

Перемещения отдельных точек тела человека рассматриваются в трехмерном пространстве — определяются их линейные перемещения относительно начала отсчета.

В большей части случаев движения звеньев в суставах рассматри­вают как вращательные и определяют угловые перемещения звеньев относительно смежных с ними.

2.3. Траектория точна

Траектория точки — это пространственная мера движения (вооб­ражаемый след движения точки)¹. Измеряют длину и кривизну траектории и определяют ее ориентацию в пространстве.

Движущаяся точка занимает ряд непрерывно сменяющихся проме­жуточных положений; ее движение образует непрерывную линию — траекторию. При движении точки ее координаты изменяются. Они становятся больше или меньше, могут менять знак на обратный.

Изменение координат точки определяет направление и величину пере­мещения

При постоянном на­правлении движения траек­тория по форме представляет пря­мую линию (прямолинейное дви­жение ²); при переменном направлении — кривую (кри­волинейное движение).

Длину траектории (расстояние вдоль нее) характеризует путь точки. При прямолиней­ном движении для определенного участка траектории (прямой линии) измеряют его длину.

При криволинейном движении вектор перемещения — хорда участ­ка криволинейной траектории—не совпадает с траекторией. Малое перемещение, при котором можно с необходимой степенью точности заменить малый участок траектории ее хордой, условимся называть элементарным перемещением (ds).

При криволинейном движении путь точки равен ариф­метической сумме модулей ее элементарных перемещений; перемещение же точки равно геометрической сумме ее элементар­ных перемещений.

Форму криволинейного движения характеризует кривизна траектории(k). Это величина, обратная радиусу кривизны траектории(R), т. е. радиусу такой элементарной дуги окружности, которой допустимо заменять соответствующий элементарный участок траектории: k=1/R

Следовательно, чем больше радиус такой дуги, тем меньше кри­визна траектории.

Для траектории любой формы определяют также ее ориентацию в пространстве: для прямой траектории — по координа­там точек начального и конечного положений, для кривой — по коор­динатам этих двух точек траектории и третьей точки, не лежащей с ними на одной прямой.

При поступательном движении тела у всех его точек траектории одинаковые. По траектории одной точки (например, ОЦТ) можно изучить движение тела. При вращательном движении тела у каждой его точки свой след в пространстве, хотя у точек с оди­наковым радиусом траектории по форме одинаковы. Здесь движение всего тела (только когда оно простое вращательное) также можно изу­чить, определив по траектории одной точки угол поворота тела.

При движении же биомеханической системы надо определить траек­тории точек ее звеньев, а также траекторию ее ОЦТ.

Траектории точек каждого звена относительно оси сустава можно приближенно считать дугами окружностей. Однако относительно осей соседних суставов или системы прямоугольных координат, связанной, например, с Землей, траектории точек имеют сложные и разнообраз­ные формы. Лишь иногда движения точек плоские. Почти всегда про­странственные (трехмерные) траектории кривые. Они, как правило, исключительно сложны для составления уравнений, описывающих закон движения³.

Таким образом, все пространственные характе­ристики — координаты, перемещения и траек­тории — в совокупности определяют начало и окончание движения и его форму в пространстве.

3. ВРЕМЕННЫЕ ХАРАКТЕРИСТИКИ

Временные характеристики совместно с пространственно-времен­ными определяют характер движений человека.

20.1. Момент времени

Момент времени (или мгновение) — это временная мера положе­ния точки, тела и системы в начале, в ходе движения и в конце. Момент времени определяется промежутком времени до него от начала отсчета (положение на оси времени)

Определяя, где была точка в пространстве, необходимо опреде­лить, когда она там была.

Момент времени нужно определять не только для начала и окончания движения, но и для других важных мгновенных поло­жений. В первую очередь это моменты существенного изменения движения: заканчивается одна часть (фаза) движения и начина­ется следующая (например, отрыв от опоры—это момент окончания фазы отталкивания и начала фазы взлета).

3.2. Длительность движения

Длительность движения — это его временная мера. Она изме­ряется разностью моментов времени окончания и начала движения в неизменной системе отсчета.

Отвечая на вопрос: «Какое расстояние в пространстве пройдено в движении?»,— необходимо выяснить и другой: «Сколько времени затрачено на это?». Из значения момента времени окончания движения вычитается значение момента времени его начала. Полученная вели­чина промежутка времени характеризует длительность движения (длительность одной фазы движения, длительность ряда фаз или период движения, например период полета). Момент времени не имеет длительности. Он служит границей двух смежных промежутков вре­мени.

Естественно, что для определения длительности движения надо пользоваться одними и теми же началом отсчета времени и единицами отсчета.

При движении могут быть и остановки (паузы, перерывы в движе­нии). Следует также измерять их длительность.

3.3. Темп движений

Темп движений—это временная мера повторности движений¹. Он измеряется количеством движений, повторяющихся в единицу времени:

При многократном повторении движений их длительность может быть одинаковой. В этих случаях понятием «темп» характеризуется протекание движения во времени.

Темп—величина, обратная длительности движений: эти понятия связаны обратно пропорциональной за­висимостью. В практических условиях темп проще определять, чем длительность. Темпы движений удобнее сравнивать, если брать более крупные единицы времени. Например, при длительности шагов лыж­ника-гонщика в 0,55 сек. и 0,51 сек. частота шагов будет 18,0 и 19,5 в 10 сек., или, что иногда удобнее для подсчета и сравнения, 108 и 117 шагов в одну минуту.

Темп движений может служить в отдельных случаях показателем совершенства владения техникой. У квалифицированных спортсменов (пловцов, гребцов, бегунов и др.) он выше, чем у неквалифицирован­ных, следовательно отдельные движения у первых чаще. На темпе движений может отражаться утомление: в одних видах движений он повышается (учащение шагов при их укорочении в беге), в других — понижается (неспособность поддерживать заданный темп, например, в гребле).

3.4. Ритм движений

Ритм движений — это временная мера соотношения частей дви­жений. Он определяется по соотношению промежутков времени, затраченного на соответствующие части движения:

Ритм определяют как соотношение двух периодов времени (напри­мер, опоры и полета в беге) или длительности двух фаз периода (на­пример, фазы амортизации и фазы отталкивания в опорном периоде). Можно говорить и о ритме ряда фаз (например, соотношение длитель­ностей пяти фаз скользящего шага в лыжном ходе).

Фазы, ритм которых изучается, могут различаться по направлению, скорости и ускорению движений, по величине и направлению усилий и по другим .характеристикам. Соотношение длительностей фаз отра­жает соотношение обусловливающих их усилий. Однако для определе­ния ритма движений необходимо измерение именно времени, а не усилий. Ритм бывает постоянным и переменным. Он может быть и в повторяющихся (циклических) и в однократных (ациклических) движениях.

С точки зрения биомеханики в каждом движении есть ритм, посколь­ку имеются различающиеся части движений определенной длитель­ности. То, что в практике называется неритмичным движением, в биомеханике следует расценивать как ритм нерационального движе­ния или несоблюдение заданного ритма.

4. ПРОСТРАНСТВЕННО-ВРЕМЕННЫЕ ХАРАКТЕРИСТИКИ

Пространственно-временные характеристики определяют изменение положения и движения человека во времени.

4.1. Скорость точки и тела

Скорость точки¹—это пространственно-временная мера дви­жения. Она определяет быстроту изменения положения точки в пространстве с изменением времени. Скорость измеряется отношением вектора элементарного перемещения (в данной сис­теме отсчета) ,к соответствующему промежутку времени: V_ср=s/t

Таким образом, скорость характеризует и быстроту, и направление движения².

Если для расчета скорости берется все время движения и соответст­вующее суммарное перемещение (путь), то получается средняя скорость на данном участке пути. Такова же скорость в любое мгновение в любой точке траектории при постоянном (равномерном и прямолинейном) движении. Но у человека, как правило, движение точек тела переменное (неравномерное и криволинейное), поэтому модуль и направление скорости в течение движения изменяются. В таком случае движение на протяжении его выполнения более точно характеризуется мгновенными скоростями.

Мгновенная скорость точки — это мера быстроты изменения по­ложения точки в данный момент времени. Она измеряется преде­лом отношения вектора перемещения к соответствующему про­межутку времени (в данной системе отсчета), когда этот промежу­ток стремится к нулю:

Скорость точки (линейная) как вектор совпадает по направлению с вектором перемещения. Это наглядно видно в прямолинейном дви­жении. В криволинейном движении вектор мгновенной скорости, как предел элементарного перемещения (величина — хорда, направле­ние — секущая), совпадает с касательной в данной точке траектории и направлен в сторону движения.

Как положение тела определяется по положению его точек, так и скорость тела определяется по скоростям его точек. При посту­пательном движении скорости всех точек тела (линейные) одинаковы. При вращательном же чем дальше точка от оси вращения (больше радиус), тем больше ее линейная скорость. Отноше­ние линейных скоростей всех вращающихся точек твердого тела к их радиусам одинаково. Эта величина — угловая скорость ()

— характеризует быстроту вращательного движения тела:  =v/r .

Отсюда линейная скорость точки вращающегося тела равна произ­ведению угловой скорости и радиуса вращения: v=wr/

Угловая скорость тела (мгновенная) — это пространственно-временная мера быстроты изменения положения тела во враща­тельном движении. Она измеряется пределом отношения углового перемещения тела (угла поворота) к соответствующему промежут­ку времени (в данной системе отсчета), когда этот промежуток стремится к нулю.
Таким образом, угловая скорость тела может быть измерена по его угловому перемещению, а также по линейному перемещению какой-либо его точки и по ее радиусу вращения (радиус траектории в данный момент). Сложное движение твердого тела можно определить по линей­ной скорости ОЦТ и угловой скорости вращения тела вокруг оси, проходящей через его ОЦТ.

Угловая скорость недеформирующейся системы тел определяется и измеряется так же, как у твердого тела. Но человек, меняя позу, представляет собою биомеханическую систему, изменяющую свою конфигурацию. В этих условиях определение скоростей вращательных движений и их измерение очень затруднено.

Вследствие вращательного характера движений звеньев в суставах направление скоростей точек всегда переменно. Благодаря тяге мышц синергистов и антагонистов под действием множества других сил мо­дули линейных скоростей точек и угловых скоростей звеньев почти не бывают постоянными.

Таким образом, скорости звеньев все время из­меняются как по направлению, так и (почти всегда) по модулю.

4.2. Ускорение точки и тела

Ускорение точки — это пространственно-временная мера изме­нения движения. Она характеризует быстроту и направление изменения вектора скорости точки в данный момент времени. Ускорение измеряется пределом отношения изменения скорости к соответствующему промежутку времени (в данной системе от­счета), когда этот промежуток стремится к нулю: a=lim v /t

Скорость точки как вектор может изменяться по модулю, по направлению или одновременно и по модулю и по направлению. Соответственно различают ускорения точки:

а) положительное, имеющее одинаковое направление со ско­ростью,— скорость возрастает; б) отрицательное, имеющее направление, противоположное направлению скорости,— скорость убывает; в) нормальное — направление его перпендикулярно направлению скорости и вектор скорости изменяет только направле­ние, не изменяя своей величины (криволинейное движение).

При поступательном движении линейное ускорение тела равно линейному ускорению любой его точки.

При вращательном движении положительное и отрицательное ускорения, направленные по касательной, называются тангенциальными, а направленные по радиусу (нормали) — радиаль­ными или нормальными. Каждое из этих ускорений может проявляться независимо. Сочетание тангенциального ускорения с нор­мальным бывает при одновременном изменении скорости и по модулю, и по направлению. Векторная сумма нормального и тангенциального ускорений определяет полное ускорение.

При вращательном движении угловое ускорение тела характери­зует изменение скорости вращения.

Угловое ускорение — это мера изменения скорости вращатель­ного движения тела в данный момент времени. Угловое ускорение определяется как предел отношения изменения угловой скорости к соответствующему промежутку времени в данной системе отсчёта¹, когда этот промежуток стремится к нулю:

Среднее ускорение за время всего движения, особенно в тех случаях, когда оно меняет знак, обычно не определяется, поскольку оно не характеризует подробности (детали) движения.

Угловое ускорение может быть либо положительным (убыстрение вращения), либо отрицательным (замедление вращения). Для вращающегося твердого тела отношения линейных ускорений точек к их радиусам вращения (расстояниям до оси) одинаковы; они равны угловому ускорению тела: a/r=

Линейное ускорение точки вращающегося тела равно произведению углового ускорения и радиуса вращения: a=r(в радианном измере­нии);

В сложном движении тела (одновременно поступательном и враща­тельном) изменения скорости измеряют линейным ускорением ОЦТ и угловым ускорением тела относительно его ОЦТ.

Определение угловых ускорений биомеханической системы еще бо­лее затруднено, чем определение угловых скоростей.

Таким образом, ускорение характеризует непостоянство скорости.

Скорости точек звеньев тела человека изменяются по модулю и направлению. Значит, всегда есть нормальные ускорения и почти всегда — тангенциальные (положительные и отрицательные). Движений тела человека без ускорений не бывает, но ускорения иногда могут оказаться настолько малыми, что практиче­ски не будут иметь значения.

5. КИНЕМАТИЧЕСКИЕ ОСОБЕННОСТИ ДВИЖЕНИЙ ЧЕЛОВЕКА

Кинематические особенности движений человека как биомеханиче­ской системы намного сложнее, чем особенности движений твердого тела. Это зависит как от механических причин, так и от биологических факторов — активности мышц.

5.1. Составное движение и его составляющие

В биомеханике удобно условно различать: а) составное движение как результат движения нескольких связанных друг с другом тел и б) сложное движение одного тела (одновременно поступательное и вращательное).

Выше говорилось о том, что сложное движение твердого тела в пространстве можно представить себе как результат сложения двух простых движений: поступательного и вращательно­го. В этом случае складываются два движения одного тела.

Но тело человека — изменяемая система, поэтому в его двига­тельной деятельности имеет место еще и сложение движе­ний различных звеньев. Например, при толкании ядра движение кисти легкоатлета относительно Земли есть результат сло­жения множества движений звеньев ноги, туловища и руки, т.е. со­ставное движение.

5.2. Сложение скоростей и ускорений в составном движении

Результирующая угловая скорость двух вращательных движений (переносного и относительного) вокруг параллельных осей равна их сумме, если вращения направлены в одну сторону, и разно­сти — если направления противоположны.

Иначе говоря, здесь имеет место алгебраическое суммирование. Результирующая угловая скорость увеличивается, когда составляю­щие ее угловые скорости направлены в одну сторону. Движение же в каком-либо сочленении в противоположную сторону уменьшает скорость конечного звена (и линейную, и угловую).

Результирующее ускорение такого составного движения, в котором переносное движение является вращательным, равно сумме трех ус­корений: переносного, относительного и поворотного:

Сложение скоростей и ускорений происходит намного сложнее, если переносное движение вращательное, а относительное — посту­пательное.

Уточним направление поворотного ускорения. При отдалении тела по радиусу от оси переносного вращения поворотное ускорение нап­равлено в сторону вращения, при приближении тела к оси вращения оно направлено в сторону, противоположную враще­нию.

Иначе говоря, при приближении тела к оси вра­щения поворотное ускорение отрицательное, при отдалении тела от оси вращения — поло­жительное (по отношению к скорости вращения).

5.3. Изменение скоростей в движениях человека

Изменениями направления и сложением скоростей движений звеньев обусловливаются возвратно-вращательный, а иногда и возвратно-поступательный, а также круговой характер движений звеньев тела человека.

При движениях звеньев в суставах движение каждого звена можно приближенно рассматривать как вращательное. Следовательно, траек­тории точек звеньев будут криволинейными и скорости будут изме­нять свое направление. Благодаря сложению движений звеньев в со­ставное движение траектории рабочих точек могут иметь очень разно­образную пространственную форму. Также весьма разнообраз­ными могут быть изменения результирующих скоростей рабочих то­чек.

Ни в одном сочленении человека и животных невозможно полное вращательное движение. Во всех одно- и двуосных суставах возможны движения вокруг осей в пределах обычно около половины окружности. Вследствие этого движения в суставах имеют возвратно-вращательный характер (со сменой направления на обрат­ное). В большинстве случаев это движения колебательного типа.

В результате пары вращений с одинаковыми по величине, но проти­воположными по направлению угловыми скоростями (например, раз­гибание в локтевом и сгибание в плечевом суставах) возникает посту­пательное движение звена или нескольких звеньев (например, движе­ние предплечья и кисти вперед). Но такое движение также ограниченное связями в суставах и потому носит возвратно-посту­пательный характер (со сменой направления на обратное). Надо подчеркнуть, что поступательным движение является относи­тельно всего тела, а в соответствующих суставах — это по-прежнему возвратно-вращательное движение.

В шаровидных суставах (плечевом, тазобедренном) возможно кру­говое движение (циркумдукция) без возвратного движения. В механике это движение рассматривается как ряд последовательных элементарных поворотов вокруг мгновенных осей вращения, прохо­дящих через сустав. Мгновенная ось все время изменяет свое направ­ление; мгновенные угловые скорости и ускорения также все время изменяются. Таким образом, круговое движение — это сложное дви­жение, состоящее из двух вращений.

Из бесчисленного множества возможных траекторий в процессе эволюции и разумного отбора закрепились в практике лишь очень немногие из возможных сочетаний. Это движения, наиболее рацио­нальные как в отношении достижения цели, так и по экономичности использования возможностей. В спортивных движениях отбираются и закрепляются самые эффективные. Поэтому здесь траектории рабо­чих точек и определяющие их скорости движений имеют более строго установленный характер, чем, например, в бытовых движениях.