Курсовая работа СМО Гангур. Курсовая работа методы решения задач оптимизации по дисциплине Методы оптимизации Направление подготовки
 Скачать 490.03 Kb. Скачать 490.03 Kb.
|
Метод идеальной точки.Метод идеальной точки состоит в отыскании на границе Парето точки, ближайшей к точке утопии, задаваемой ЛПР. Обычно ЛПР формулирует цель в виде желаемых значений показателей, и часто в качестве координат целевой точки выбирается сочетание наилучших значений всех критериев (обычно эта точка не реализуется при заданных ограничениях, поэтому ее и называют точкой утопии). В этом разделе лекции мы подробно рассмотрим метод идеальной точки на следующем конкретном примере. Пусть на множестве ω плоскости (OXY) определяемом системой неравенств: 0≤x≤4; 0≤y≤2; x+2y≤6; Заданы две линейные функции: U (x, y) = x+y+2; V (x, y) = x–y+6. Требуется найти решение задачи U = Φ (x, y) → max, V = Ψ (x, y) → max,(x, y) ω. Множество ω представляет собой пятиугольник ABCDE, вершины которого имеют следующие координаты: A (0,0), B (0,2), C (2,2), D (4,1), E (4,0). 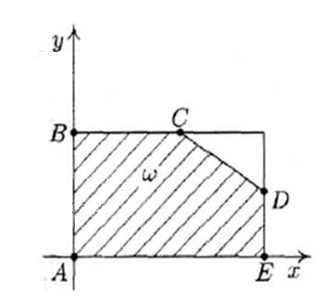 Рисунок 1 – Метод идеальной точки. В силу линейности критериев U и V пятиугольник ABCDE на плоскости OXY переходит в пятиугольник A*B*C*D*E* на плоскости OUV, координаты вершин которого вычисляются по следующим формулам (3): A*=(U(A), V(A)) = (U (0,0), V (0,0)) = (2,6); B*=(U(B), V(B)) = (U (0,2), V (0,2)) = (4,4); C*=(U(C), V(C)) = (U (2,2), V (2,2)) = (6,6); D*=(U(D), V(D)) = (U (4,1), V (4,1)) = (7,9); E*=(U(E), V(E)) = (U (4,0), V (4,0)) = (6,10). Теперь находим границу Парето: это отрезок D*E*. Точка утопии М*(7,10) считается заданной (ее координаты равны, соответственно, наибольшим значениям U и V). Из (Рис. 2) ясно, что UM*=UD*=7, VM*=VE*=10 в системе координат OUV. 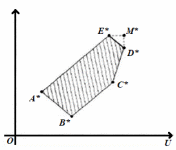 Рисунок 2 – Построение границы Парето множества Ω. Требуется найти на множестве Парето точку, ближайшую к точке утопии М*. Из рисунка 2 видно, что искомая точка должна лежать на отрезке D*E*. Проведем через точки D* и Е* прямую (D* E*). Найдем уравнение этой прямой. Пусть уравнение прямой (D* E*) в системе координат (OUV) имеет вид: α∙U+β∙V = γ. Чтобы отыскать конкретные значения параметров α, β и γ, подставим в него координаты обеих точек – и D*,и Е*. Получим следующую систему уравнений. (D*): α∙7+β∙9=γ, (E*): α∙6+β∙10=γ. Вычитая из первого равенства второе, после простых преобразований придем к соотношению: α – β=0. Отсюда, α=β. Положим α=β=1, тогда γ=16. Следовательно, искомое уравнение прямой (D*E*): U+V=16. Напомним, как найти расстояние между точками, заданными своими координатами в декартовой прямоугольной системе координат. Пусть M1(U1, V1) и M2(U2, V2) – две точки на плоскости (OUV). Для того чтобы найти расстояние между ними, достаточно вычислить длину гипотенузы построенного прямоугольного треугольника. Воспользовавшись теоремой Пифагора, получим для гипотенузы |M1M2| построенного прямоугольного треугольника: |M1M2|2 = (U2 – U1)2+(V2 – V1)2. По условию задачи нам нужно определить на прямой (D*E*), заданной уравнением U + V= 16, точку М0(U0, V0), расстояние которой от точки М*(7,10) минимально, то есть решить экстремальную задачу: f (U, V) = (U – 7)2+(V– 10)2→min. Так как U = 16 – V, то последнее соотношение можно переписать в виде: f(U(V), V) ≡ F(V) = (9 –V)2+(V– 10)2→min. Отсюда, возводя в квадрат и приводя подобные, получаем: F(V)=2V2 – 38V+181 → min. Это уравнение описывает параболу с вершиной (V0, F(V0)), где координата V0 находится из условия равенства нулю производной: F`(V)= 4V – 38 =0. То есть V0=19/2, тогда F(V0) = 2(19/2)2 – 38∙19/2+181=1/2. Таким образом, идеальная точка М0(U0, V0) находится на расстоянии √F(V0) = 1/√2 от точки утопии М*(7,10) (Рис. 3). Чтобы найти координату U0, рассмотрим уравнение прямой (D*E*), на которой лежит идеальная точка М0(U0, V0): U+V=16. Отсюда, U0+V0=16. Следовательно, U0+19/2=16, U0=16 – 19/2=13/2. Таким образом, M0 = (13/2; 19/2). 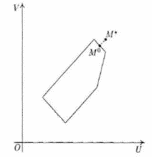 Рисунок 3 – Нахождение идеальной точки. Возвращаясь к системе координат OXY, заметим, что соответствующие значения x0 и y0 легко находятся из системы линейных уравнений: U0 = x0+y0 – 6, V0 = x0 – y0 +2. Здесь мы воспользовались равенствами: U0 = U (x0, y0), V0 = V (x0, y0). Имеем: 13/2= x0+y0 + 6, 19/2= x0 – y0 +2. Складывая уравнения, получим: 16=2x0 + 8, то есть x0 =4. Вычитая из первого уравнения второе уравнение, получим: - 3=2y0 – 4, то есть y0=1/2. Значит, идеальная точка на плоскости OXY имеет координаты: (4; 1/2). |
