Курсовая работа СМО Гангур. Курсовая работа методы решения задач оптимизации по дисциплине Методы оптимизации Направление подготовки
 Скачать 490.03 Kb. Скачать 490.03 Kb.
|
Пример 1 (продолжение).Сформулируем задачу многокритериальной оптимизации (1), (2) для примера 1. Вектор X= {x} переменных задачи имеет одну действительную компоненту x. Множество допустимых решений Q = [0, L/2] – отрезок действительной прямой OX. Первый частный критерий Z1 – действительная функция V(x): Z1(x) = V(x) = (L – 2x)2∙x. Второй частный критерий Z2 – действительная функция (– 1) ∙S(x): Z2(x)= (– 1) ∙S(x)= – 4x2. Заметим, что при задании критерия Z2 мы поменяли у функции S(x) знак на противоположный, так как в примере 1 функция S(x) минимизируется, а в задаче (1), (2) каждый критерий максимизируется. При этом условия Z2(x)→max, и S(x)→min равносильны. Вектор критериев имеет вид: Z(X) = {Z1(X); Z2(X)} = {V(x); – S(x)} = {(L – 2x)2∙x; – 4x2}. Таким образом, мы получаем следующую задачу многокритериальной оптимизации: Z(x) = {(L – 2x)2∙x; – 4x2} →max, (1’) при условии x[0; L/2]. (2’) Многокритериальная задача выбора решения в общем виде состоит в выборе некоторого допустимого вектора X из множества Q на основе анализа вектора критериев Z(X).При этом предполагается, что вектор критериев Z(X) полностью описывает интересующие ЛПР аспекты принятия решения. Оптимальность по Парето.Определение:Вектор X*, принадлежащий множеству допустимых решений Q, называется эффективным (оптимальным) по Пареторешением задачи многокритериальной оптимизации (1), (2), если не существует такого вектора Xиз множестваQ, что выполняются неравенства: Zi(X) ≥ Zi(X*), (i =1, …, m,)(3) причем хотя бы для одного значения j, где 1≤j≤ m, имеет место строгое неравенство: Zj(X) > Zj(X*). Определение:Если для допустимых решений X(1), X(2)задачи многокритериальной оптимизации (1), (2) выполнены условия: Zi(X (1)) ≥Zi (X (2)), (i=1,2, ..., m); и при этом существует такой критерийZj, где1 ≤ j ≤ m, что выполнено строгое неравенство: Zj (X (1)) > Zj (X (2)), то говорят, что допустимое решение X (1) доминирует допустимое решение X (2). Другими словами, будем говорить, что решение X (1) из множества допустимых решений Q в задаче многокритериальной оптимизации (1), (2) доминирует решение X(2) из того же множества Q, если X (1) по каждому из критериев не хуже X (2), и при этом хотя бы по одному из критериев – строго лучше. В соответствии с введенным определением решения, оптимального по Парето, получим, что решение X* из множества допустимых решений Q задачи многокритериальной оптимизации (1), (2) будет оптимальным по Парето, если не существует допустимых решений, которые бы его доминировали. Геометрическое изображение множества Парето называется Парето-эффективной границей (Парето-оптимальной границей). В задаче многокритериальной оптимизации наилучшее решение следует искать в множестве Парето. Алгоритм построения Парето-эффективной границы: Строим допустимое множество D, заданное системой ограничений как пересечение полуплоскостей, соответствующих каждому неравенству, входящему в эту систему. Для каждой функции 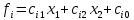 строим линию уровня как прямую, перпендикулярную соответствующему вектору нормали строим линию уровня как прямую, перпендикулярную соответствующему вектору нормали 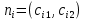 . .Каждая из этих линий разбивает плоскость XOY на две полуплоскости. Пусть Пi – полуплоскости, содержащие вектор градиента целевой функции fi, а их пересечение 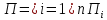 Перемещая данную область П по границе допустимого множества D, находим те точки границы, которые являются единственными точками пересечения областей П и D. Данные точки - оптимальные по Парето, а множество всех таких точек – Парето-эффективная граница. |
