Курсовая работа СМО Гангур. Курсовая работа методы решения задач оптимизации по дисциплине Методы оптимизации Направление подготовки
 Скачать 490.03 Kb. Скачать 490.03 Kb.
|
Решение.Задана следующая модель регрессии: 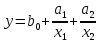 где 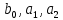 - параметры, для которых необходимо найти оценку (значения - параметры, для которых необходимо найти оценку (значения 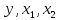 нам известны). Заданная функция нам известны). Заданная функция 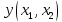 не зависит от искомых параметров, следовательно необходимо построить такую функцию, которая будет от них зависеть. не зависит от искомых параметров, следовательно необходимо построить такую функцию, которая будет от них зависеть. Поскольку необходимо найти вид заданного уравнения, то целесообразно будет считать квадраты отклонений между исходными данными 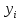 и заданным уравнением с параметрами и заданным уравнением с параметрами 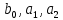 . Отсюда можно найти функцию, зависящую от заданных параметров: . Отсюда можно найти функцию, зависящую от заданных параметров: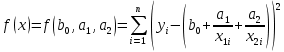 где x – искомая 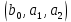 точка; точка; 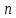 – количество наблюдений. Теперь оценку параметров можно искать как точку минимума заданной функции – количество наблюдений. Теперь оценку параметров можно искать как точку минимума заданной функции 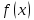 , т. е. задача сводится к минимизации суммы квадратов отклонений предполагаемой прямой и исходных точек. Поскольку задача приняла вид , т. е. задача сводится к минимизации суммы квадратов отклонений предполагаемой прямой и исходных точек. Поскольку задача приняла вид 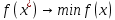 , то теперь можно приступить к ее решению методом простого градиентного спуска. , то теперь можно приступить к ее решению методом простого градиентного спуска. Компоненты градиент функции 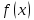 : :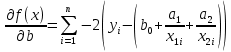 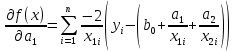 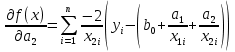 Коэффициент детерминации.Коэффициент детерминации модели показывает ее степень зависимости от заданных параметров (факторов). Коэффициент принимает значения от 0 до 1, и чем он ближе к единице, тем сильнее представленная зависимость. В случае регрессионных моделей, чем ближе коэффициент к единице, тем сильнее модель соответствует исходным данным. Поскольку регрессионная модель не является линейной, то коэффициент детерминации вычисляется по следующей формуле: 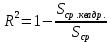 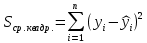 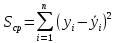 где 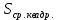 – сумма квадратов отклонений исходных значений – сумма квадратов отклонений исходных значений 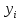 и искомой функции и искомой функции 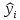 ; ; 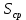 – общая сумма квадратов между исходными данными – общая сумма квадратов между исходными данными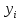 и их средним значением и их средним значением 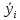 ; ;Код Matlab.clc; clear all format compact X = dlmread('table.txt'); b = 3; a1 = -2; a2 = 1; t_k = 0.0001; eps = 0.00001; h = 0; M = 5000; figure plot(0, 0); hold on; while sqrt(dF_b(b, a1, a2, X).^2+dF_a1(b, a1, a2, X).^2+dF_a2(b, a1, a2, X).^2)>eps if h < M f_k = F(b, a1, a2, X); b_new = b - t_k*dF_b(b, a1, a2, X); a1_new = a1 - t_k*dF_a1(b, a1, a2, X); a2_new = a2 - t_k*dF_a2(b, a1, a2, X); f_KK=F(b_new, a1_new, a2_new, X); plot(h, f_KK, '.r', 'markersize', 5); if f_KK > f_k t_k = t_k/2; end if (sqrt((b_new - b)^2 + (a1_new - a1)^2 + (a2_new - a2)^2) < eps & abs(f_KK - f_k) < eps) break; end else break; end b = b_new; a1 = a1_new; a2 = a2_new; h = h + 1; end xlim([0 h]);ylim([0 5]); fprintf('Получены следующие результаты: \n b=%f \n a1=%f \n a2=%f', b, a1, a2); fprintf('\n \n Количество итераций: %d \n', h); R = f_KK; fprintf('Сумма квадратов отклонений равна: %f \n', R);R_d = det(X, f_KK); fprintf('Коэфициент детерминации равен: %f \n', R_d); function y = F(b, a1, a2, X) j = size(X,1); S = 0; for i = 1:j S = S + (X(i,3) - b - a1/X(i,1) - a2/X(i,2)).^2; end y = S; end function y = dF_b(b, a1, a2, X) j = size(X,1); S = 0; for i=1:j S = S - 2*(X(i,3) - b - a1/X(i,1) - a2/X(i,2)); end y = S; end function y = dF_a1(b, a1, a2, X) j = size(X,1); S = 0; for i = 1:j S = S + 2*(-1/X(i,1))*(X(i,3) - b - a1/X(i,1) - a2/X(i,2)); end y = S; end function y = dF_a2(b, a1, a2, X) j = size(X,1); S = 0; for i = 1:j S = S + 2*(-1/X(i,2))*(X(i,3) - b - a1/X(i,1) - a2/X(i,2)); end y = S; end function y = det(X, SS_res) j = size(X,1); SS = 0; y_sr = 0; for i = 1:j y_sr = y_sr + X(i, 3); end y_sr = y_sr/j; for i = 1:j SS = SS + (X(i,3) - y_sr).^2; end y = 1 - SS_res/SS; end |
