Курсовая работа СМО Гангур. Курсовая работа методы решения задач оптимизации по дисциплине Методы оптимизации Направление подготовки
 Скачать 490.03 Kb.
|
Пример 2.Решить задачу многокритериальной оптимизации методом идеальной точки: 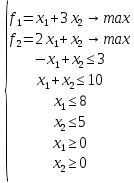 Решение: По условию задачи область допустимых решений задана системой неравенств: 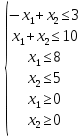 Построим данную область: 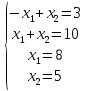 В качестве допустимого множества получаем область OABCDE с угловыми точками O(0;0), A(0;3), B(2;5), C(5;5), D(8;2), E(8;0). 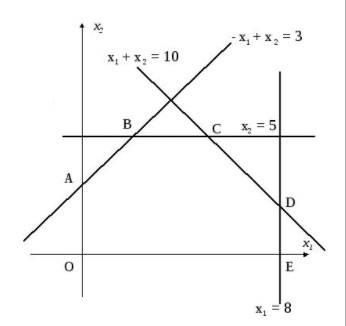 Рисунок 4 – График области OABCDE. 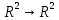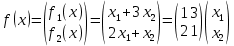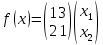Введем линейное преобразованиеf:  , определенное критериями f1 и f2:  При этом: 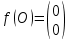 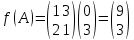 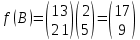 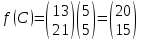 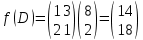 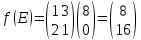 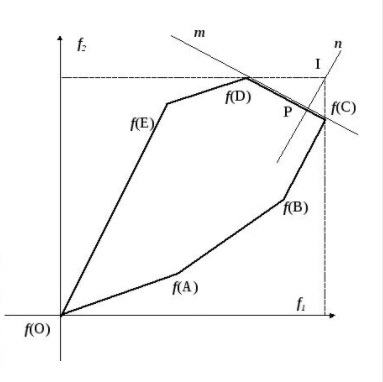 Рисунок 5 – Образ области D. По причине линейности f строим образ области D под действием преобразования f на плоскости (f1; f2) – шестиугольник с вершинами f(O), f(A), f(B), f(C), f(D), f(E). Идеальная точка – I с координатами (f1max; f2max), которая не принадлежит образу D. Компромиссной точкой является т. P, принадлежащая D и ближайшая к I – основание перпендикуляра, опущенного из I на отрезок, соединяющий точки f(C) и f(D). Найдем уравнение прямой m, проходящей через две данные точки, затем уравнение прямой n и получим координаты точки P как 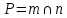 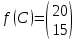 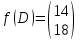 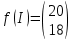 Уравнение прямой m: 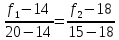 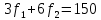 Уравнение нормали: 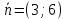 Уравнение прямой n: 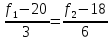 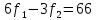 Решим систему уравнений: 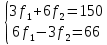 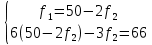 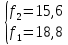 Найдем компромиссную точку как прообраз P: 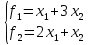 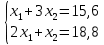 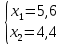 Ответ: 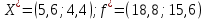 |