Курсовая работа СМО Гангур. Курсовая работа методы решения задач оптимизации по дисциплине Методы оптимизации Направление подготовки
 Скачать 490.03 Kb. Скачать 490.03 Kb.
|
Строительная задача.Строительной кампании поступил заказ на производство двух видов бетонных плит. Для производства первого вида необходимо 30 кг. песка и 10 кг. цемента. Для производства второго – 20 кг. песка и 20 кг. цемента. У кампании на складе имеется запас 1000 кг. песка и 800 кг. цемента. Стоимость первого вида бетонных плит за штуку равна 5$., а второго – 8$. Необходимо выполнить заказ, максимизируя прибыль и количество произведенных плит. 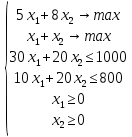 Решение: Построим данную область на графике: 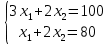 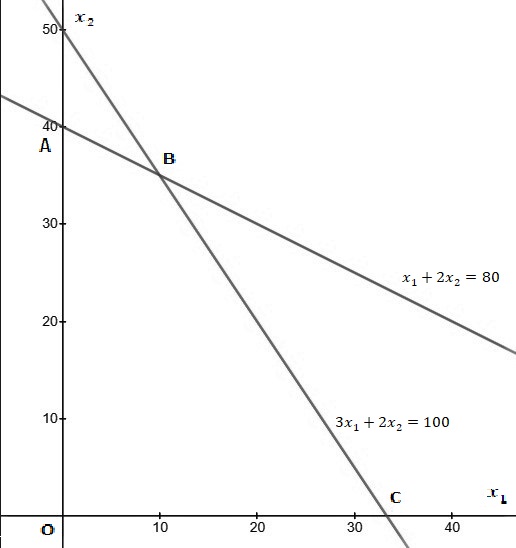 Рисунок 7 – Область OABC. В качестве допустимого множества получаем область OABC с угловыми точками O(0;0), A(0;40), B(10;35), C(33,33;0). Введем линейное преобразованиеf: 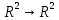 , определенное критериями f1 и f2: , определенное критериями f1 и f2: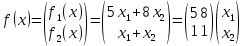 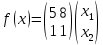 При этом: 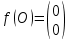 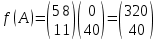 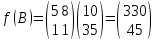 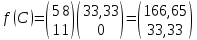 По причине линейности f строим образ области D под действием преобразования f на плоскости (f1; f2) – четырехугольник с вершинами f(O), f(A), f(B), f(C). 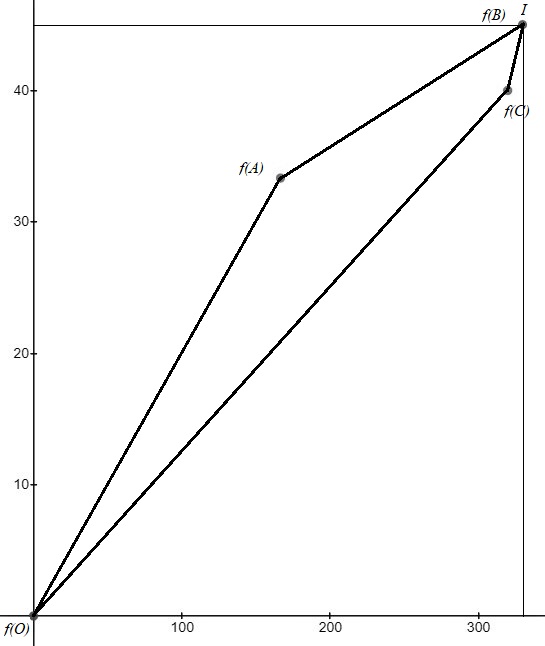 Рисунок 6 – Образ области. Идеальная точка – I с координатами (330; 45), которая принадлежит образу D и находится в точке f(B). Ответ: 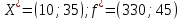 Постановка задачи.При помощи метода простого градиентного спуска найти оценку параметров заданной регрессионной модели с заданной точностью 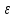 . Оценить качество полученных оценок, найдя сумму квадратов отклонений и индекс детерминации. . Оценить качество полученных оценок, найдя сумму квадратов отклонений и индекс детерминации.Метод простого градиентного спуска.Пусть дана функция 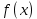 , для которой необходимо найти локальный минимум на множестве допустимых решений , для которой необходимо найти локальный минимум на множестве допустимых решений 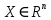 , т. е. найти такую точку , т. е. найти такую точку 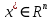 , что , что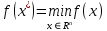 Суть метода состоит в построении последовательности точек 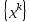 таких, что таких, что 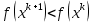 . Точки последовательности вычисляются по следующей формуле: . Точки последовательности вычисляются по следующей формуле: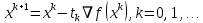 (1.1) (1.1)где точка 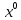 задается пользователем; задается пользователем; 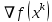 – градиент функции – градиент функции 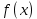 , вычисленный в точке , вычисленный в точке 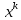 ; ; 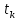 – величина шага, задаваемая пользователем, которая остается постоянной до тех пор, пока функция убывает в точках последовательности, что контролируется проверкой выполнения неравенства – величина шага, задаваемая пользователем, которая остается постоянной до тех пор, пока функция убывает в точках последовательности, что контролируется проверкой выполнения неравенства 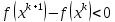 . Построение последовательности точек заканчивается в точке . Построение последовательности точек заканчивается в точке 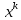 , если выполняется одно из нескольких условий окончания. , если выполняется одно из нескольких условий окончания.Алгоритм: Задать 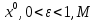 – предельное число итераций. Найти градиент функции в произвольной точке – предельное число итераций. Найти градиент функции в произвольной точке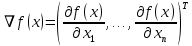 Положить k=0 Вычислить 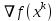 Проверить выполнение критерия окончания 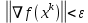 : : а) если выполняется, то закончить расчет и искомая точка 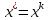 ; ;б) иначе перейти к шагу 5; Проверить выполнение неравенства 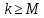 А) если выполняется, то закончить расчет и искомая точка 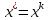 ; ;Б) иначе перейти к следующему шагу; Задать величину шага 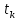 Вычислить 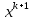 по формуле (1.1) по формуле (1.1)Проверить выполнение условия 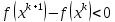 а) если условие выполнено, то перейти к шагу 9; б) иначе положить 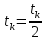 и вернуться к 7 шагу; и вернуться к 7 шагу;Проверить выполнение условий 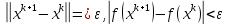 а) если оба условия выполняются при текущем значении k и k=k-1, то окончить расчет и положить искомую точку 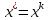 ; ;б) если хотя бы одно условие не выполняется, то положить k=k+1 и перейти к шагу 3; 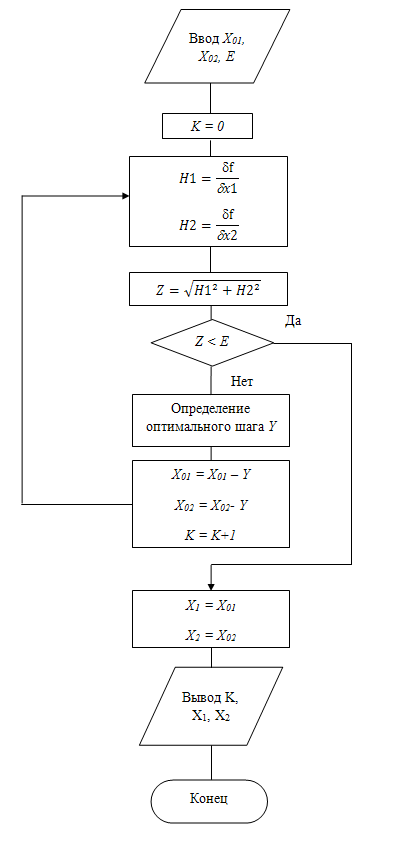 Рисунок 8 - Блок схема метода простого градиентного спуска. У метода простого градиентного спуска есть несколько недостатков. Во-первых, метод может медленно (или даже очень медленно) сходится. Это может быть связанно с неудачно подобранной начальной точкой 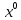 , либо из-за слишком маленького (большого) шага , либо из-за слишком маленького (большого) шага 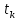 , либо из-за очень маленькой заданной точности , либо из-за очень маленькой заданной точности 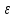 . Во-вторых, метод очень плохо работает с “овражными” функциями (кратко: функции, у которых линии уровней сильно вытянуты, имеют странную форму или много локальных минимумов). С такими функциями метод либо очень медленно сходится, либо вовсе не находит точку оптимума (происходит бесконечное зацикливание или уходит на минимум, не являющийся оптимальным). . Во-вторых, метод очень плохо работает с “овражными” функциями (кратко: функции, у которых линии уровней сильно вытянуты, имеют странную форму или много локальных минимумов). С такими функциями метод либо очень медленно сходится, либо вовсе не находит точку оптимума (происходит бесконечное зацикливание или уходит на минимум, не являющийся оптимальным). |
