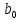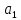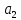Курсовая работа СМО Гангур. Курсовая работа методы решения задач оптимизации по дисциплине Методы оптимизации Направление подготовки

• Название: Курсовая работа методы решения задач оптимизации по дисциплине Методы оптимизации Направление подготовки
• Дата: 09.06.2022
• Размер: 490.03 Kb.
• Имя файла: Курсовая работа СМО Гангур.docx
• Тип: Курсовая; #582321
• страница: 9 из 9

Пример 2 Matlab.

Данные, находящиеся в файле table.txt, предоставлены в (таблице 3.)

x1	x2	у
1	1	0.10
2	2	0.15
3	3	0.20
4	4	0.25
5	5	0.30
6	6	0.35
7	7	0.40
8	8	0.45
9	9	0.50
10	10	0.55
11	11	0.60
12	12	0.65
13	13	0.70
14	14	0.75
15	15	0.80
16	16	0.85
17	17	0.90
18	18	0.95
19	19	0.99

Таблица 3 – Исходные данные.

Для данного примера были заданы следующие начальные параметры: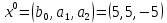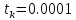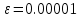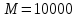

• 
  
  
• 
  
  
• 
  
  
• 
  
  

Получены следующие результаты:

b=0.722465

a1=4.538736

a2=-5.461264

Количество итераций: 8746

Сумма квадратов отклонений равна: 0.691013

Коэффициент детерминации равен: 0.512029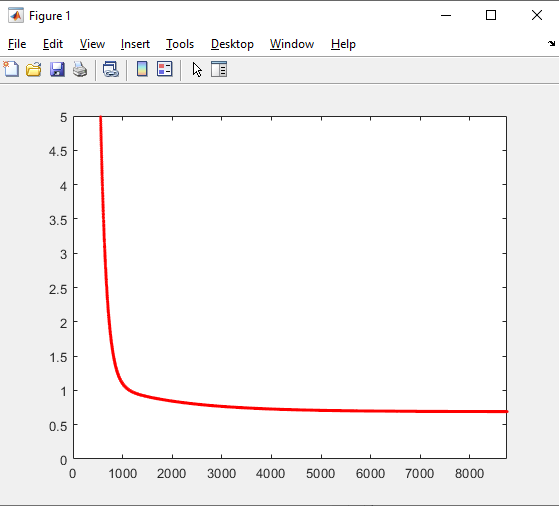

>>



Рисунок 12 – Сумма квадратов отклонений.

Из полученных результатов можно составить уравнение регрессионной модели: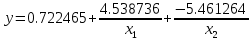

Пример 2 Excel.

Для реализации решения другим инструментальным средством будет использоваться Excel. Заполняем ячейки Excel исходными данными, а затем на их основе формируем сумму квадратов отклонений и целевую функцию (в ячейке D21 находится целевая функция, а все что выше – квадраты отклонений для каждого исходного данного).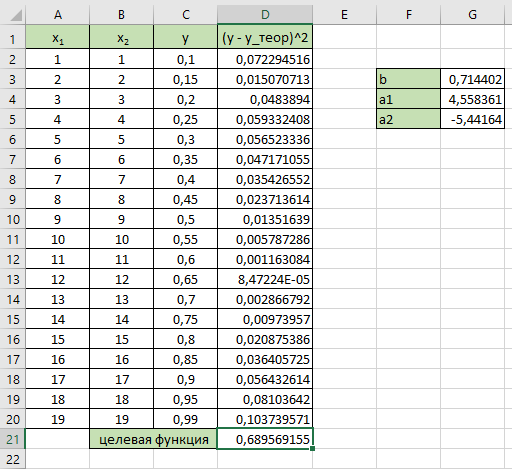



Рисунок 13 – Таблица Excel.

Вызываем “Поиск решения”, указываем все необходимое, нажимаем “найти решение” и получаем ответ.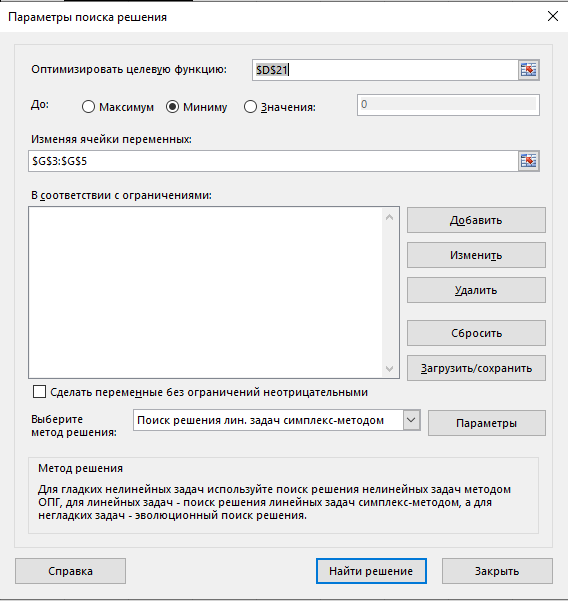



Рис.14 – “Поиск решения”.

В результате работы Excel получаем следующую функцию: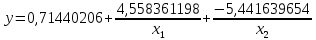

				Сумма квадратов
Excel	0,71440206	4,558361198	-5,441639654	0,689569155
Matlab	0.722465	4.538736	-5.461264	0.691013

Таблица 4 – сравнение Matlab и Excel.

Сравнивая результаты, мы видим, что данные практически совпадают. Matlab справился с работой чуть лучше.

Пример 3 Matlab.

Данные, находящиеся в файле table.txt, предоставлены в (таблице 5.)

x1	x2	у
1,01	5,55	0,06
1,02	5,56	0,07
1,03	5,57	0,08
1,04	5,58	0,09
1,05	5,59	0,10
1,06	5,60	0,11
1,07	5,61	0,12
1,08	5,62	0,13
1,09	5,63	0,14
1,10	5,64	0,15
1,11	5,65	0,16
1,12	5,66	0,17
1,13	5,67	0,18
1,14	5,68	0,19
1,15	5,69	0,20
1,16	5,70	0,21
1,17	5,71	0,22
1,18	5,72	0,23
1,19	5,73	0,24
1,20	5,74	0,25
1,21	5,75	0,26
1,22	5,76	0,27

Таблица 5 - Исходные данные.

Для данного примера были заданы следующие начальные параметры: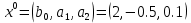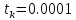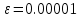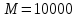

• 
  
  
• 
  
  
• 
  
  
• 
  
  

Получены следующие результаты:

b=1.239551

a1=-1.185663

a2=-0.034547

Количество итераций: 828

Сумма квадратов отклонений равна: 0.000406

Коэффициент детерминации равен: 0.995414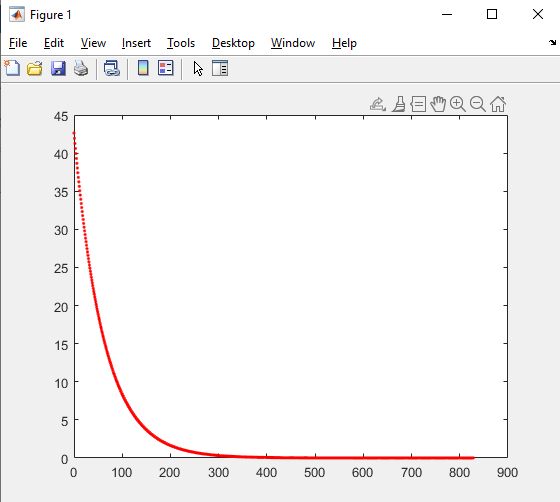

>>



Рисунок 15 – Сумма квадратов отклонений.

Из полученных результатов можно составить уравнение регрессионной модели: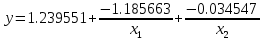

Пример 3 Excel.

Для реализации решения другим инструментальным средством будет использоваться Excel. Заполняем ячейки Excel исходными данными, а затем на их основе формируем сумму квадратов отклонений и целевую функцию (в ячейке D21 находится целевая функция, а все что выше – квадраты отклонений для каждого исходного данного).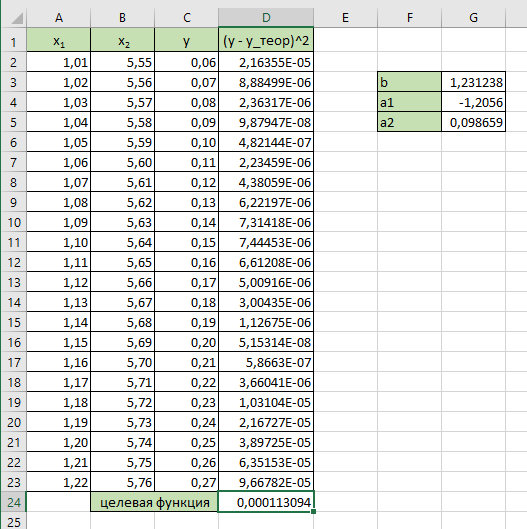



Рисунок 16 – Таблица Excel.

Вызываем “Поиск решения”, указываем все необходимое, нажимаем “найти решение” и получаем ответ.



Рисунок 17– “Поиск решения”.

В результате работы Excel получаем следующую функцию: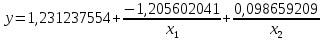

				Сумма квадратов
Excel	1,231237554	-1,205602041	0,098659209	0,000113094
Matlab	1.239551	-1.185663	-0.034547	0.000406

Таблица 6 – сравнение Matlab и Excel.

Сравнивая результаты, мы видим, что данные практически совпадают. Excel справился с работой лучше.

Заключение.

В ходе выполнения курсовой работы были изучены два метода оптимизации – метод идеальной точки и метод простого градиентного спуска. Были изучены теоретические аспекты обоих методов, а также применение их на практике для решения различных задач с использование различного программного обеспечения.

Метод идеальной точки был реализован без использования сторонних программируемых приложений. Метод градиентного спуска был реализован в среде Matlab и результаты, полученные с помощью него, были проверены при помощи Microsoft Excel и его инструментария в виде “Поиска решений”.

Источники. 

1. 
   https://www.bibliofond.ru/view.aspx?id=864672
   
2. 
   https://myslide.ru/presentation/skachat-dinamicheskoe-programmirovanie-seminar-3
   
3. 
   Таха Х.А. Введение в исследование операций. — 6-е изд. Пер. с англ. — М.: Издательский дом «Вильямс», 2001. — 912 с: ил.
   
4. 
   Фомин Г. П. Математические методы и модели в коммерческой деятельности: Учебник. — 2-е изд., перераб. и доп. — М.: Финансы и статистика, 2005. — 616 с: ил.
   
5. 
   Шелобаев С. И. Математические методы и модели в экономике, финансах, бизнесе: Учебное пособие для вузов. — М.: ЮНИТИ - ДАНА, 2001. - 367 с.
   
6. 
   Шикин Е. В., Чхартишвили А. Г. Математические методы и модели в управлении: Учебное пособие. — 3-е изд. — М.: Дело, 2004. — 440 с. — (Серия «Классический университетский учебник»).
   
7. 
   Методы оптимизации Практический курс – А.В. Пантелеев, Т.А. Летова – 2011