Курсовая. для курсача1. Курсовая работа. Методика обучения учащихся доказательству теорем студентка 141 гр
 Скачать 179.5 Kb. Скачать 179.5 Kb.
|
|
Глава 2. Методика обучения доказательству теорем Этапы работы с теоремами. Приемы мотивации изучения и доказательства теорем Изучая методы работы учителей можно выяснить, чем достигается успех. Ученики формально усваивают материал обычно у тех учителей, которые излагают теоремы догматически. Учитель сообщает формулировку теоремы, сам приводит её доказательство, которое затем повторяется несколькими учениками. Если в процессе доказательства педагог задает детям вопросы, то чаще всего они касаются формулировок ранее пройденных теорем и определений, но не вскрывают путей к отысканию доказательства. Учащимся непонятно, почему появилась именно эта теорема, зачем делается то или иное дополнительное построение. Совсем иначе идет работа у тех учителей, которые привлекают школьников к разбору содержания теоремы и к самостоятельным поискам тех логических связей, на которых построено ее доказательство. Такая творческая работа вызвает интерес учащихся и тем самым повышает активность их внимания. Результатом является не пассивное запоминание, а усвоение самого смысла доказательства. Изучение каждой теоремы дает возможность поставить перед учениками две задачи: 1) выявить некоторые свойства изучаемого объекта и 2) логически обосновать необходимость этих свойств. [гастева,с.517] Г.И. Саранцев [сар.,70] выделяет следующие этапы изучения теоремы: Мотивация изучения теоремы. Ознакомление с фактом, отраженным в теореме. Формулировка теоремы и выяснение смысла каждого слова в формулировке теоремы. Усвоение содержания теоремы; Запоминание формулировки теоремы; Ознакомление со способами ее доказательства; Доказательство теоремы; Применение теоремы; Установление связей теоремы с ранее изученными теоремами. Главным, по мнению автора, в изучении теорем является не заучивание их и их доказательств, а открытие школьниками теоремы, способа доказательства, самостоятельное конструирование доказательства, применение теоремы, применение теоремы в различных ситуациях, установление связей с другими теоремами. Примеры: С теоремой о сумме углов треугольника учащиеся могут ознакомиться, измеряя непосредственно углы треугольника. Обобщая результаты измерений, учащиеся приходят к выводу, что сумма углов треугольника равна 1800. Чтобы помочь учащимся самостоятельно найти путь дедуктивного обоснования догадки, можно предложить решить задачу. Задача. Через вершину треугольника проведена прямая, параллельная основанию. Доказать, что углы, образованные этой прямой с боковыми сторонами треугольника, соответственно равны углам треугольника при основании. Решение этой задачи открывает путь доказательства сформулированной догадки. Для закрепления можно предложить следующие задачи [погор, с. 63]: Угол АВС равен 80о, а угол ВСР равен 120о. Могут ли прямые АВ и СР быть параллельными? Обоснуйте ответ. Найдите угол между боковыми сторонами равнобедренного треугольника, если угол при основании равен: 1) 40о; 2) 55о; 3) 72о. Основное свойство степени с натуральным показателем учащиеся могут выделить, выполнив упражнение: «Представьте в виде степени с показателем, отличным от единицы, произведение: а) х2?х3; б) bb2b5». После выполнения нескольких подобных упражнений учащиеся замечают, что произведение двух степеней с одинаковыми основаниями равно степени с тем же основанием и показателем, равным сумме показателей этих степеней. Для усвоения содержания теоремы можно использовать упражнения на выделение условия и заключения теоремы; на вычленение на чертежах, моделях таких фигур, которые удовлетворяли бы условию теоремы. Саранцев Г.И. [12] предлагает пользоваться следующей схемой (схема 1): Схема 2:
В целях облегчения запоминания громоздких формулировок теорем целесообразно поэлементное усвоение содержания теоремы. Для этого формулировка теоемы разбивается на отдельные элементы, после чего каждый из элементов используется при выполнении упражнений. При индуктивном введении теоремы Лященко Е. И. [9] условно выделяет следующие этапы ее изучения: Мотивация изучения теоремы и раскрытие ее содержания (Усмотрение геометрического факта и формулировка теоремы); Работа над структурой теоремы; Мотивация неоходимости доказательства теоремы; Построение чертежа и краткая запись содержания теоремы; Поиск доказательства, доказательство и его запись; Закрепление теоремы; Применение теоремы. Для мотивации необходимости изучения теорем можно предложить такие приемы: Прием 1. Обощение наблюдаемых в жизни фактов и явлений и перевод их на математический язык. Мотивировать необходимость изучения свойства «Две прямые либо не пересекаются, либо пересекаются только в одной точке» можно, преложив предварительно учащимся решить дома следующие задачи: А) На плане местности четыре населенных пункта отмечены точками A,B,C,K. Выясните, пересекутся ли пути из пункта А в пункт С и из пункта K в пункт В. Если пересукуться, то в скольких точках? Рассмотрите различные возможные случаи расположения населенных пунктов. Могут ли эти пути пересечься в двух точках? В классе учитель выясняет полученные результаты решения задачи: во всех случаях пути движения либо имеют одну общую точку, либо е имеют ни одной. Отметив, что пути движения в данных задачах были отрезки, предпалагается подумать над вопросом: изменится ли вывод, если вместо отрезков взять две прямые? Этот прием можно использовать при изучении многих теорем. Прием 2. Показ необходимости знания той или иной теоремы для решения практических задач. Для мотивации изучения теоремы «Если две стороны и угол между ними одного треугольника равны соответственно двум сторонам и углу между ними другого треугольника, то такие треугольники равны» можно использовать следующую задачу: Картографам необходимо нанести на карту два населенных пункта А и В (рис. 7). Измерить расстояние между пунктами оказалось невозможно так как между ними было озеро. Картографы поступили следующим образом: они выбрали точку С от которой можно было измерить расстояние и до пункта А, и до пункта В. Измерили эти расстояния и построили на бумаге отрезки АС и АВ соответствующей длины (масштаб можно указать по своему усмотрению) а затем продолжили линии за точку С, отложили отрезки СН и СМ, равные соответственно отрезкам СВ и СА, и соединили точки Н и М отрезком. Картографы считают, что расстояние АВ и НМ равны между собой. Правы ли картографы? - По условию задачи известно, что АС=СМ, ВС=СН и, кроме того как вертикальные углы. - Надо установить, что АВ=НМ. - Откуда может следовать равенство этих отрезков? - Равенство отрезков АВ и НМ может следовать из равенства треугольников АСВ и МСН. - Но в равных треугольниках соответственно равны все шесть элементов (три стороны и три угла), а здесь мы имеем только две стороны и угол между ними одного треугольника соответственно равные двум сторонам и углу между ними другого треугольника. Как быть? - Следует доказать, что если две стороны и угол между ними одного треугольника соответственно равны двум сторонам и углу между ними другого треугольника, то такие треугольники равны. Мотив и необходимость доказательства теоремы показаны. Прием 3. Показ необходимости знания той или иной теоремы для решения задач и доказательства других теорем. Прием 4. Показ, как решалась данная проблема в истории науки. Например, рассмотрим доказательство формулы (а + b)2 = a2 +2ab +b2. У древних греков величины обозначались не числами или буквами, а отрезками прямых. Они говорили не “а2”, а “квадрат на отрезке а”, не “ab”, а “прямоугольник, заключенный между отрезками a и b”. Первым с доказательством этой формулы столкнулся древнегреческий учёный Евклид, живущий в Александрии в III веке до н.э., так как в те времена не было букв, он пользовался геометрическим способом доказательства формулы. 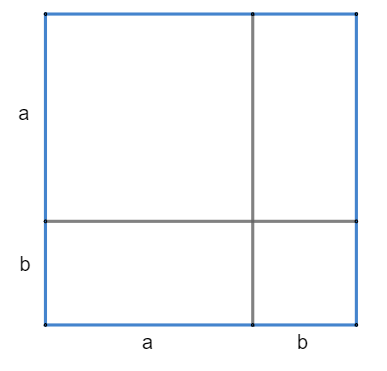 Из данного рисунка видно, что площадь квадрата со стороной (а + b) равна сумме площадей квадрата со стороной а, квадрата со стороной b и двух прямоугольников с длиной а и шириной b. Если прямая линия (имеется в виду отрезок) разделен на 2 отрезка а и b, то квадрат на всей прямой, т.е. (а + b)2 равен а2 + b2 + 2ab. Значит, (а + b)2 = a2 +2ab +b2 Очевидно, что перечисленные приемы для мотивации изучения теорем служат одновременно и раскрытию содержания теоремы. Из других приемов раскрытия содержания теорем можно назвать: Наблюдение наглядного материала, в том числе подвижных моделей или ряда чертежей; Выполнение постороений; Решение задач на вычисление и доказательство; Выполнение лабораторных и практических работ; Решение задач на отыскание некоторых зависимостей. Пример: Для раскрытия содержания теоремы Фалеса можно использовать следующий прием: начертить в тетрадях угол (произвольный); отложить на одной стороне угла последовательно несколько равных отрезков через концы отрезков провести параллельные прямые до пересечения со второй стороной угла; измерить отрезки, получившиеся на второй стороне угла, и сравнить их между собой. После этой работы высказывается предположение (формулируется теорема), которое затем доказывается [9, с. 53]. Методика организации работы с теоремами при изучении курса геометрии в 7-9 классах Доказательство теоремы в учебниках дается почти всегда сплошным текстом, но учителю следует расчленить доказательство на части, на отдельные логические шаги. Надо составить план доказательства и продумать рациональную запись доказательства теоремы. Возможны две формы записи доказательства теоремы. Одна из них состоит в том, что вначале записывается полученный вывод и здесь же в строчку записываются аргументы, на основе которых он был сделан. Другая форма предполагает заполнение таблицы. Рассмотрим работу по обучению доказательству теорем на примере некоторых теорем из курса геометрии основной школы. В 9 классе изучается теорема косинусов. Раскроем методические особенности работы с этой теоремой. Будем работать с данной теоремой, применяя частично-поисковый метод обучения [cайт], то есть, учитель учит учеников самостоятельно выполнять отдельные шаги в целостном процессе познания. Задача учителя при применении частично-поискового метода - научить учеников самостоятельно применять знания, вести поиск новых. Этот метод применяется при опоре на уже имеющиеся у учащихся знания и умения. Чаще всего метод реализуется с помощью проблемных, творческих заданий, способ выполнения которых учащимся не известен. Перед доказательством теоремы школьникам можно предложить найти сторону треугольника, зная две другие и угол между ними. В процессе анализа данной задачи выходим на существование теоремы косинусов. Квадрат стороны треугольника равен сумме квадратов двух других сторон минус удвоенное произведение этих сторон на косинус угла между ними. Обозначим имеющиеся данные: Пусть в АВ = с, ВС = a, СА = b. Докажем, что . Для доказательства воспользуемся методом введения декартовой системы координат с началом в точке А так, как показано на рисунке 9 [геом.257]. Во время доказательства теоремы учитель задает вопросы детям: Как определить координаты точки В? (так как АВ = с, следовательно В (с; 0)). Как найти координаты точки С? (провести высоту к АВ, через геометрический смысл синуса и косинуса угла А найти координаты точки). Найдем расстояние между двумя точками В и С откуда получим искомое выражение.[геом, с. 258] Теорему косинусов также называют обобщенной теоремой Пифагора. Такое название объясняется тем, что в теореме косинусов содержится как частный случай теорема Пифагора. В самом деле, если в треугольнике ABC угол А прямой, то и тогда воспользовавшись теоремой получим , т.е. теорему Пифагора. Для первичного осмысления и применения изученного материала, учащимся можно предложить задания [11урок]: Задача 1 Ответ: . Задача 2 Ответ: 60°. Для закрепления полученных знаний проведем короткий тест: 1. Закончи предложение. Квадрат любой стороны треугольника равен … а) сумме квадратов двух других сторон, минус произведение этих сторон на косинус угла между ними; б) сумме квадратов двух других его сторон; в) сумме квадратов двух других сторон без удвоенного произведения этих сторон на косинус угла между ними. 2. Заполни пропуски. В треугольнике KHT . а) KH; б) HT; в) TK. 3. В треугольнике CDO известны стороны CD и CO. Величину, какого угла необходимо знать, чтобы найти длину стороны DO? а) C; б) D; в) O. 4. Дан треугольник DEF. Выберите верное равенство: а) ; б) ; в) . Для тех учеников, у которых уровень владения материалом выше, а так же для актуализации знаний на следующие темы, можно предложить следующее домашнее задание: доказать данную теорему векторным способом, в помощь предоставить таблицу [1, с. 97]. Доказательство:
Работу над доказательством теорем можно осуществлять по-разному. Для примера разберем доказательство теоремы «В равнобедренном треугольнике медиана, проведенная к основанию, является биссектрисой и высотой». |
