МЕТОДЫ РЕШЕНИЯ СИСТЕМ АЛГЕБРАИЧЕСКИХ УРАВНЕНИЙ. курсовая методы (1). Курсовая работа по дисциплине (модулю) Теория и методика обучения математике методы решения систем алгебраических уравнений
 Скачать 72.03 Kb. Скачать 72.03 Kb.
|
ОГЛАВЛЕНИЕВВЕДЕНИЕ 3 ГЛАВА 1. ПРЯМЫЕ МЕТОДЫ РЕШЕНИЯ СИСТЕМ АЛГЕБРАИЧЕСКИХ УРАВНЕНИЙ 5 1.1 Матричный метод 6 1.2 Метод Крамера 9 1.3 Метод Гаусса (прямой и обратный ход) 10 1.4 Метод прогонки 13 ГЛАВА 2. ИТЕРАЦИОНАЛЬНЫЕ МЕТОДЫ РЕШЕНИЯ СИСТЕМ АЛГЕБРАИЧЕСКИХ УРАВНЕНИЙ 18 2.1 Метод простых итераций (метод Якоби) 18 2.2 Метод итерации Гаусса - Зейделя 21 ЗАКЛЮЧЕНИЕ 27 СПИСОК ЛИТЕРАТУРЫ 29 ВВЕДЕНИЕ Решение систем линейных алгебраических уравнений представляет большое значение в практике вычислений. Так, линейное приближение многих математических моделей реальных объектов приводит к системам линейных алгебраических уравнений. Задачи решения таких систем возникают при обработке экспериментальных данных, приближенном решении линейных интегральных и дифференциальных уравнений и в других областях. Практические способы решения зависят от структуры исходных данных, порядка матрицы коэффициентов, а также типа используемых вычислительных средств. В настоящее время большое внимание уделяется пересмотру методов численного анализа и созданию новых алгоритмов, позволяющих наиболее эффективно использовать параллельные вычисления. В значительной мере это связано с развитием параллельных вычислительных систем с большим числом одновременно работающих процессоров [6]. В настоящее время применяется множество различных программ (MathCAD, MathLAB и т.д.), с помощью которых легко решаются различные задачи, используя только входные данные. Их применение значительно сокращает время и ресурсы для решения ряда важных задач. Тем не менее, использование этих программ без тщательного анализа метода, с помощью которого решается задача, не дает гарантии, что задача решена правильно. Поэтому в первую очередь необходимо теоретически изучить методы их решения и на практике их проработать. Это обуславливает актуальность данной работы. При решении систем линейных алгебраических уравнений возникает необходимость выбора того или иного метода, который позволит получить эффективный результат с использованием вычислительной техники. В этой ситуации актуализируется проблема сравнительного анализа прямых и итерационных методов решения. Исследованию методов решения систем линейных алгебраических уравнений уделяется большое внимание в современной математике. Среди ученых, научные интересы которых посвящены этой проблеме, необходимо выделить С. Годунова, В. Воеводина, А. Островского, Дж. Форсайта, К. Молера и др. При этом, сравнению итерационных и прямых методов решения с помощью вычислительной техники уделяется не достаточно внимания. Объектом исследования данной работы выступают системы линейных алгебраических уравнений. Предмет исследования – практические методы решения систем линейных алгебраических уравнений. Цель курсовой работы – овладение методами решения систем линейных алгебраических уравнений. Для достижения поставленной цели следует решить ряд задач: изучить научную и учебную литературу по теме «Прямые и итерационные методы решения систем линейных алгебраических уравнений»; продемонстрировать на примерах использование методов. Методы исследования: анализ, сравнение. Во введении обоснована актуальность темы курсовой работы, определены объект, предмет, цель и задачи исследования. В первой главе дан обзор прямых методов решения систем алгебраических уравнений и приведены примеры их применения. Во второй главе рассматриваются итерационные методы решения линейных алгебраических уравнений в теории и на практике. В заключении подведены итоги и сделаны основные выводы. ГЛАВА 1. ПРЯМЫЕ МЕТОДЫ РЕШЕНИЯ СИСТЕМ АЛГЕБРАИЧЕСКИХ УРАВНЕНИЙ Идею общего метода решения систем линейных уравнений высказал Лейбниц в 1693 году. Она была реализована швейцарским математиком Крамером в 1752 году. Он сформулировал и обосновал правило, носящее теперь его имя, которое позволяет решать системы n линейных уравнений с n неизвестными и буквенными коэффициентами [9]. По правилу Крамера каждая неизвестная равна отношению двух определителей. Крамер, фактически, заложил основы теории определителей, хотя и не предложил для них удобного обозначения (это сделал в 1841 году А. Кэли). В 1772 году Вандермонд опубликовал обширное исследование определителей, один из которых носит теперь его имя. Систематическое изложение этой теории принадлежит Бине и Коши. Их труды по теории определителей относятся к периоду 1812-1815 гг. Коэффициенты системы линейных уравнений и свободные члены удобно сводить в таблицы, называемые матрицами системы. Постепенно определители систем стали относить к матрицам систем. Матричный метод решения систем линейных уравнений впервые описан в древнекитайском трактате «Девять книг о математическом искусстве» (II век до н.э.). Система линейных уравнений в этом трактате записывается в виде матрицы, столбцы которой составлены из коэффициентов при неизвестных и свободных членов, и решается методом исключения, впоследствии заново сформулированном Гауссом в 1849 году. Этот метод естественно формулируется в виде правил преобразования так называемой расширенной матрицы системы. Системы линейных уравнений широко используются в задачах экономики, физики, химии и других науках. Решение систем линейных алгебраических уравнений - одна из основных задач вычислительной линейной алгебры. Хотя задача решения именно системы линейных уравнений сравнительно редко представляет самостоятельный интерес для прикладных задач, но от умения эффективно решать данные системы часто зависит сама возможность математического моделирования самых разнообразных процессов с применением ЭВМ. Значительная часть численных методов решения различных (в особенности - нелинейных) задач включает в себя решение систем линейных уравнений как элементарный шаг соответствующего алгоритма. Методы решения систем линейных алгебраических уравнений можно разбить на две группы [4]. К первой группе принадлежат так называемые точные или прямые методы – алгоритмы, позволяющие получить решение системы за конечное число арифметических действий. К таким методам относятся: метод Гаусса и метод Крамера. В методе Гаусса, например, работают над расширенной матрицей системы. А в методе Крамера – с определителями системы, образованными по специальному правилу. Вторую группу составляют приближенные методы, в частности итерационные. Матричный метод решения систем алгебраических уравнений Метод применяется для решения систем алгебраических уравнений вида: 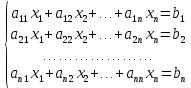 (1) (1)В матричной форме уравнения записываются как 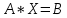 , (2) , (2)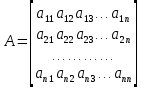 , ,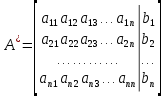 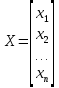 , , 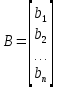 А – основная матрица системы, А* - расширенная матрица системы, Х – матрица-столбец неизвестных переменных, В – матрица свободных членов. Матричный метод может применяться в решении систем линейных алгебраических уравнений, в которых число неизвестных равно числу уравнений, то есть систем линейных уравнений с квадратной матрицей коэффициентов при неизвестных. Другими словами, когда мы говорим о главной матрице системы линейных уравнений, то всегда имеем в виду квадратную матрицу 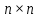 , т. е. матрицу с одинаковым количеством строк и столбцов. , т. е. матрицу с одинаковым количеством строк и столбцов. Если, например, количество строк (количество уравнений в системе) будет меньше, чем количество столбцов (фактически, количества неизвестных), то система будет неопределенной, т. е. мы не сможем однозначно определить все неизвестные (решить систему). Но это не единственное ограничение. Из векторной алгебры известно, что система линейных уравнений имеет решение (однозначное) тогда и только тогда, когда ее главный определитель не равен нулю: Δ ≠ 0. Рассмотрим случай, когда определитель системы равен нулю. Здесь возможны два варианта: Δ = 0 и каждый из дополнительных определителей Δxi= 0. Это имеет место только тогда, когда коэффициенты при неизвестных xi пропорциональны, т. е. каждое уравнение системы получается из первого уравнения умножением обеих его частей на число k. При этом система имеет бесчисленное множество решений. Δ = 0 и хотя бы один дополнительный определитель Δxi ≠ 0. Это имеет место только тогда, когда коэффициенты при всех неизвестных xi, пропорциональны. При этом получается система из противоречивых уравнений, которая не имеет решений. Для нахождения решения системы уравнений матричным методом необходимо обе части уравнения умножить на матрицу, обратную матрице коэффициентов при неизвестных и приравнять соответствующие элементы полученных матриц: 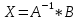 Алгоритм решения разберем на следующем примере системы линейных уравнений. Любую линейную систему уравнений можно записать в матричном виде. Например, пусть дана система: 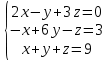 Эта система из двух уравнений с тремя неизвестными: x, y, z. Запишем эту систему в матричном виде: 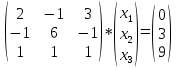 Здесь главная матрица системы и определитель: 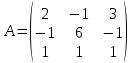 , , 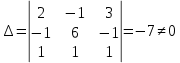 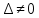 , значит система уравнений имеет однозначное решение. , значит система уравнений имеет однозначное решение.Обратная матрица будет иметь вид: 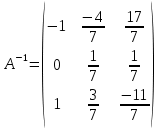 Исходная матрица неизвестных: 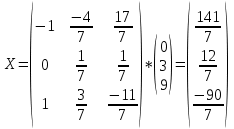 1.2 Метод Крамера Метод Крамера — способ решения систем линейных алгебраических уравнений с ненулевым определителем основной матрицы. Если определитель равен нулю, то система несовместна и данный метод решения не подходит, нужно использовать метод Гаусса [12]. Теорема Крамера. Если определитель матрицы системы не равен нулю, то система совместна и имеет единственное решение, которое находится по формулам Крамера: 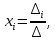 где 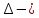 определитель матрицы системы, определитель матрицы системы, 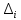 - определитель матрицы системы, где вместо i- го столбца стоит столбец правых частей. - определитель матрицы системы, где вместо i- го столбца стоит столбец правых частей.Рассмотрим метод Крамера для систем уравнений вида (1). Определитель основной матрицы равен: 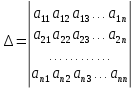 Проверяем условие 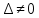 . .Для решения нам понадобится вычислить определители 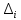 : :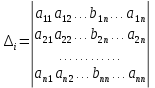 Тогда решение системы уравнений будет выглядеть так: 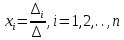 Рассмотрим пример: решить систему линейных уравнений 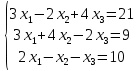 Определитель основной матрицы: 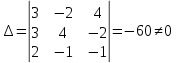 Найдем определители 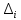 : :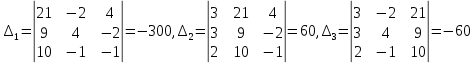 Тогда решение системы уравнений будет: 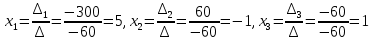 1.3 Метод Гаусса – прямой и обратный ход Рассмотрим метод Гаусса. Например, пусть дана расширенная матрица некоторой системы m линейных уравнений c n неизвестными [7]: 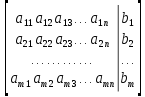 Будем считать, что a11 ≠ 0 (если это не так, то достаточно переставить первую и некоторую другую строку расширенной матрицы местами). Проведем следующие элементарные преобразования: 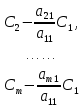 т.е. 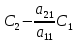 , i= 2, 3, ..., m – от каждой строки расширенной матрицы (кроме первой) отнимаем первую строку, умноженную на частное от деления первого элемента этой строки на диагональный элемент а11. , i= 2, 3, ..., m – от каждой строки расширенной матрицы (кроме первой) отнимаем первую строку, умноженную на частное от деления первого элемента этой строки на диагональный элемент а11.В результате получим матрицу: 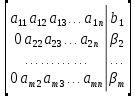 Первая строка осталась без изменений, а в столбце под а11 на всех местах оказались нули. Обратим внимание, что преобразования коснулись всех элементов строк, начиная со второй, всей расширенной матрицы системы. Теперь наша задача состоит в том, чтобы получить нули подо всеми диагональными элементами матрицы А – aij, где I = j. Повторим наши элементарные преобразования, но уже для элемента a22. 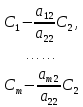 т.е. 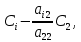 i = 3, ...,m – от каждой строки расширенной матрицы (теперь кроме первой и второй) отнимаем вторую строку, умноженную на частное от деления первого элемента этой (текущей) строки на диагональный элемент a22. i = 3, ...,m – от каждой строки расширенной матрицы (теперь кроме первой и второй) отнимаем вторую строку, умноженную на частное от деления первого элемента этой (текущей) строки на диагональный элемент a22.Такие преобразования продолжаются до тех пор, пока матрица не приведется к верхнее - треугольному виду, т.е. под главной диагональю не окажутся все нули: 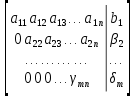 Вспомнив, что каждая строка представляет собой одно из уравнений линейной системы уравнений, легко заметить, что последнее m-ое уравнение принимает вид: 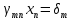 Отсюда легко можно найти значение первого корня – xn = δm/γmn. Подставив это значение в предыдущее m-1-е уравнение, легко получим значение xn-1-ого корня. Таким образом, поднимаясь до самого верха обратным ходом метода Гаусса, мы последовательно найдем все корни системы уравнений. Для обзора применения данного метода рассмотрим систему уравнений: 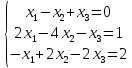 Главный определитель данной системы: 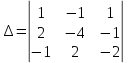 Δ =5, т. е. система определена и разрешима. Решим ее по методу Гаусса. Проведем прямой ход метода Гаусса, выписав предварительно расширенную матрицу системы: 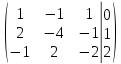 Получим нули под главной диагональю в первом столбце расширенной матрицы. 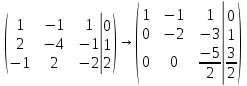 Таким образом, проведя прямой ход метода Гаусса, мы получили расширенную матрицу системы, приведенную к верхне-треугольному виду. Эта матрица эквивалентна системе: 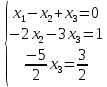 Обратным ходом метода Гаусса найдем корни системы. Из последнего уравнения найдем корень х3. Корень x3 = -3/5 найден. Подставим его во второе уравнение системы, тогда x2 = 2/5. И найдем последний корень x1 = 1. Таким образом, метод Гаусса (или метод последовательного исключения неизвестных) состоит в следующем: путем элементарных преобразований систему уравнений приводят к эквивалентной ей системе с верхнее - треугольной матрицей. Эти действия называют прямым ходом; из полученной треугольной системы переменные находят с помощью последовательных подстановок (обратный ход). 1.4 Метод прогонки Системы линейных уравнений с трехдиагональной матрицей коэффициентов при неизвестных являются наиболее важным и распространенным случаем систем специального вида [6]. В таких системах отличны от нуля только элементы, лежащие на главной диагонали и на нижней и верхней диагоналях, прилегающих к ней. К системам с трех диагональными матрицами приводят, например, задачи о сплайн-интерполяции, о решении разностными методами обыкновенных дифференциальных уравнений и уравнений в частных производных. Метод прогонки принадлежит к числу прямых методов решения систем линейных уравнений и используется в тех случаях, в которых многие коэффициенты матрицы равны нулю. Это обстоятельство учтено при реализации метода прогонки, в котором исключаются преобразования с нулевыми элементами. В методе прогонки применительно к системе линейных уравнений, имеющих трехдиагональную матрицу, можно выделить следующие этапы: 1) приведение трехдиагональной матрицы к верхней треугольной (прямой ход). В случае трехдиагональной матрицы это означает приведение к двухдиагональной, т. е. приведение исходной системы к системе, содержащей по два неизвестных в каждом уравнении, кроме последнего, в котором содержится только одно неизвестное; 2) запись обратного хода; 3) вывод рекуррентного соотношения; 4) осуществление обратного хода метода прогонки и определение всех неизвестных. Рассматриваемый метод прогонки представляет собой модификацию метода исключения Гаусса, использующую специальный регулярный вид матрицы системы. Итак, это простой и эффективный алгоритм решения систем линейных алгебраических уравнений с трехдиагональными матрицами: 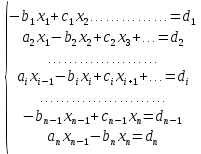 Или 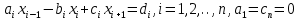 Прямой ход метода прогонки сводится к исключению неизвестного в каждом уравнении системы. Получаемая в результате прямого хода система содержит в каждом уравнении только два неизвестных и матрица ее — верхняя треугольная с двумя диагоналями. Запишем i-ю строку преобразованной двухдиагональной матрицы в виде: 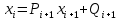 Построим эффективную вычислительную схему, которая и составляет суть метода прогонки через 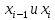 : подставляем : подставляем 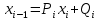 в систему: в систему: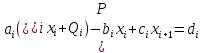 , ,откуда: 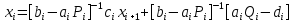 , ,Рекуррентные соотношения: 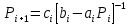 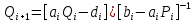 После прямого хода матрица коэффициентов будет иметь вид: 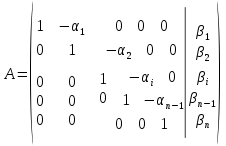 Откуда находим 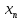 , и далее обратным ходом через рекуррентные соотношения последовательно находим , и далее обратным ходом через рекуррентные соотношения последовательно находим 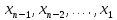 . .Пример. Решить систему уравнений методом подгонки: 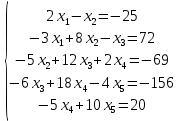 Расширенная матрица коэффициентов имеет вид: 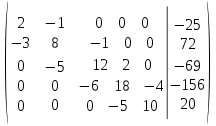 В условии этой задачи система задана именно такой матрицей, т.е. ненулевые элементы стоят на главной диагонали и на двух её окружающих. Общий вид уравнение в системе: 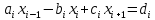 Прямой ход: 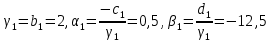 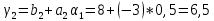 , , 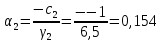 , , 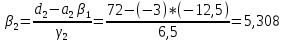 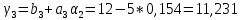 , , 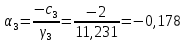 , , 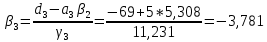 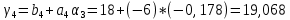 , , 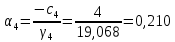 , , 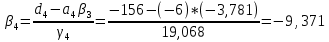 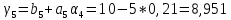 , ,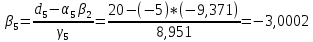 После прямого ходя матрица принимает вид 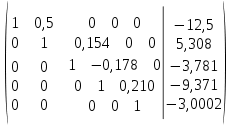 Получим 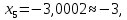 формула для обратного хода: формула для обратного хода: 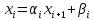 : :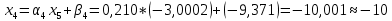 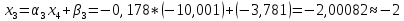 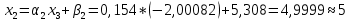 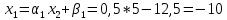 Проверяем: 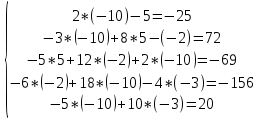 Система уравнений решена верно. ГЛАВА 2. ИТЕРАЦИОНАЛЬНЫЕ МЕТОДЫ РЕШЕНИЯ СИСТЕМ АЛГЕБРАИЧЕСКИХ УРАВНЕНИЙ Итерационные методы решения систем линейных алгебраических уравнений позволяют получить значения искомых неизвестных в результате многократного выполнения единообразных шагов, называемых последовательными приближениями или итерациями [11]. В отличие от прямых методов решение можно получить только с заданной конечной точностью, причем с увеличением требуемой точности растет и количество итераций. В итерационном процессе матрица коэффициентов системы уравнений не подвергается преобразованиям, что позволяет максимально использовать ее слабую заполненность. Однако общее число итераций, как правило, значительно больше порядка n решаемой системы уравнений. 2.1 Метод простых итераций (метод Якоби) Итерационные методы в отличие от точных методов позволяют за конечное число шагов m достичь 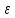 -окрестности решения системы, где -окрестности решения системы, где 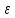 – заданная точность [5]. Число шагов или итераций m определяется выбором начального приближения – заданная точность [5]. Число шагов или итераций m определяется выбором начального приближения 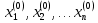 , погрешностью , погрешностью 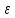 и зависит от коэффициентов матрицы системы. и зависит от коэффициентов матрицы системы.Для проведения итерационного процесса система (2) записывается в виде 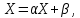 где 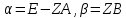 Матрица Z выбирается так, чтобы выполнялось достаточное условие сходимости метода простых итераций: 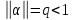 Нормой вектора B и матрицы A называются соответственно следующие числа: 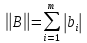 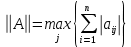 Процесс последовательного приближения по методу простых итераций может быть построен в соответствии с формулами 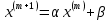 где начальное приближение есть столбец свободных членов: 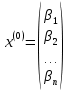 Если 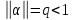 , последовательность , последовательность 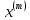 сходится по норме к истинному решению сходится по норме к истинному решению 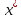 , т.е , т.е 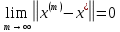 и справедливы оценки: и справедливы оценки:апостериорная 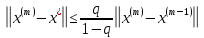 априорная 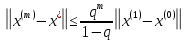 Из априорной оценки следует, что для достижения требуемой точности 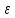 необходимо выполнить количество итераций m, которое является ближайшим натуральным числом, превышающим: необходимо выполнить количество итераций m, которое является ближайшим натуральным числом, превышающим: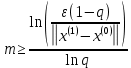 Апостериорная оценка, как правило, используется в качестве практического критерия остановки итерационного процесса. Если 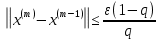 требуемая точность 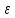 достигнута и процесс последовательного приближения к решению достигнута и процесс последовательного приближения к решению 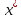 прекращают. прекращают.Условие окончания итерационного процесса при достижении точности 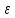 имеет вид: имеет вид: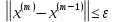 Практическое применение данного метода решения рассмотрим на системе уравнений, для которого необходимо найти приближенное решение, сделав три итерации: 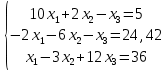 Прежде чем применять метод итераций, необходимо переставить строки исходной системы таким образом, чтобы на диагонали стояли наибольшие по модулю коэффициенты матрицы. Достаточным условием сходимости метода простой итерации является диагональное преобладание в матрице А (каждый диагональный элемент должен быть больше суммы модулей недиагональных элементов соответствующей строки или столбца). Для нашей задачи условие сходимости выполняется. Приведем систему уравнении к виду: 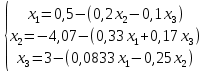 Начальное приближение 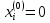 , , Вычисления при первой итерации m=1 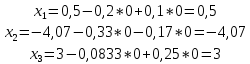 Вычисления при второй итерации m=2 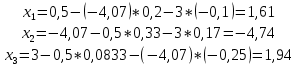 Вычисления при третьей итерации m=3 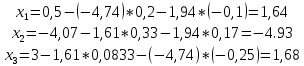 Ответ: 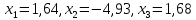 2.2 Метод итерации Гаусса - Зейделя Процесс итерации Якоби иногда можно модифицировать для ускорения сходимости [10]. Данный метод является одним из самых распространенных итерационных методов решения систем линейных алгебраических уравнений, поскольку он отличается простотой и легкостью программирования. Метод заключается в следующем: допустим, диагональные коэффициенты исходной матрицы 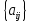 отличны от нуля (в противном случае можно переставить местами уравнения исходной системы). Представим исходную систему (1) в следующем виде: отличны от нуля (в противном случае можно переставить местами уравнения исходной системы). Представим исходную систему (1) в следующем виде: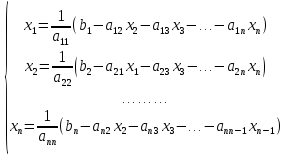 (3) (3)Если теперь задать для неизвестных их начальные приближенные значения 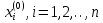 то система (3) позволяет вычислить более точные значения неизвестных на первом шаге (на первой итерации): 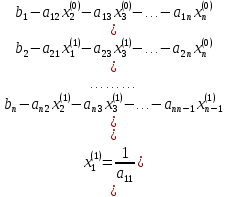 Используя найденные значения неизвестных, можно еще более уточнить их на второй итерации: 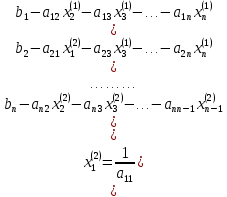 В данном методе для нахождения значения i-го неизвестного на каждой итерации используются значения предыдущих неизвестных, уже найденные на данной итерации. Общую формулу определения i-го неизвестного на k-й итерации для системы n уравнений можно записать так: 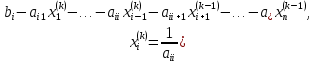 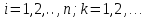 Итерационный процесс продолжается до тех пор, пока все значения 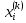 не станут достаточно близкими к не станут достаточно близкими к 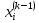 . Близость этих значений можно охарактеризовать максимальной абсолютной величиной их разности ẟ. Тогда при заданной точности вычислений ℇ>0 критерий окончания итерационного процесса можно записать в виде: . Близость этих значений можно охарактеризовать максимальной абсолютной величиной их разности ẟ. Тогда при заданной точности вычислений ℇ>0 критерий окончания итерационного процесса можно записать в виде: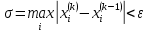 При выполнении этого условия итерационный процесс называется сходящимся. В этом случае максимальные разности между значениями соответствующих неизвестных в двух последовательных итерациях убывают, а сами значения стремятся к решению системы. Доказано, что для сходимости итерационного процесса достаточно, чтобы модули диагональных коэффициентов для каждого уравнения были не меньше суммы модулей всех остальных коэффициентов: 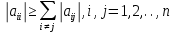 При этом хотя бы для одного уравнения данное неравенство должно выполняться строго. Таким образом, способ итераций дает возможность получить последовательность приближенных значений, сходящихся к точному решению системы. Для этого система приводится к заданному виду. При этом, чтобы итерационный процесс сходился к точному решению, достаточно, чтобы все коэффициенты системы были малы по сравнению с диагональными. Это условие можно сформулировать и более точно: для сходимости процесса итераций достаточно, чтобы в каждом столбце сумма отношений коэффициентов системы к диагональным элементам, взятым из той же строки, была строго меньше единицы: 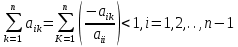 Следует так же сказать, что итерационный процесс может проводиться как в виде итерации Якоби, так и в виде итерации Гаусса-Зейделя. В последнем случае сходимость итерационного процесса может существенно улучшиться. Рассмотрим пример применения. Методом Зейделя решить с точностью 0,01 систему линейных уравнений, приведя ее к виду, удобному для итерации [9]. 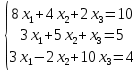 Расчетные формулы имеют вид: 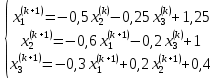 Начальное приближение 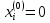 Первое приближение k= 0: 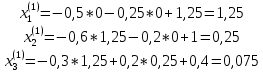 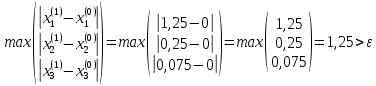 Второе приближение k = 1: 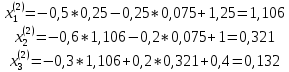 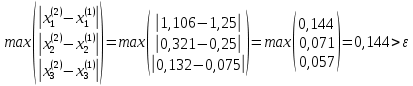 Третье приближение k = 2: 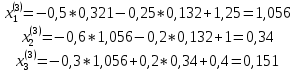 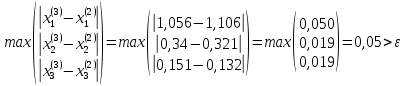 Четвертое приближение k = 3: 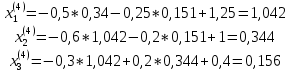 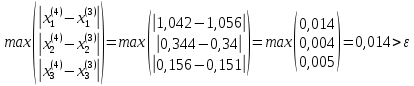 Пятое приближение k = 4: 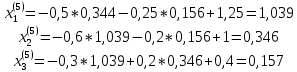 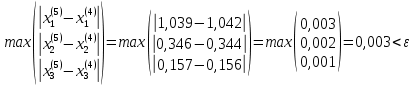 Результаты приведем в виде таблицы 1. Таблица 1 Решение систем уравнений на каждом шаге итерации
Так, на пятом приближении k=4 точность равна 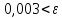 , решение: , решение: 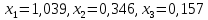 . .ЗАКЛЮЧЕНИЕ Системы линейный алгебраических уравнений можно решать, как с помощью прямых, так и итерационных методов. Прямые методы используют определенные соотношения (формулы) для вычисления неизвестных. Они дают решение после выполнения заранее известного количества арифметических операций. Так, прямыми называются численные методы, в которых: требующееся для решения задачи число арифметических операций можно оценить по расчетным формулам заранее, до начала решения; решение является точным. Эти методы сравнительно просты и наиболее универсальны, т.е. пригодны для решения широкого класса линейных систем. Для систем уравнений средней размерности чаще используют именно прямые методы. Итерационные методы применяют главным образом для решения задач большой размерности, когда использование прямых методов невозможно из-за необходимости выполнения чрезмерно большого числа арифметических операций. Итерационными называются численные методы, обладающие следующими особенностями: решение находится с помощью последовательных приближений — итераций, начиная с некоторого начального приближения («0-й итерации»), которое должно быть задано (выбрано) заранее; решение является приближенным, но с любой заданной погрешностью; требуемое для достижения заданной погрешности число итераций, а, следовательно, и число арифметических операций определяется в ходе счета и заранее не известно. Итерационные методы обычно устойчивее прямых к погрешностям округлений, так как эти погрешности постоянно корректируются в ходе итераций наряду с другими типами погрешностей. Различают одношаговые и многошаговые итерационные методы. В одношаговых методах для вычисления очередной итерации достаточно знания одной, предыдущей итерации, тогда как в многошаговых методах используются несколько предыдущих итераций. Применение итерационных методов для качественного решения большой системы уравнений требует серьезного использования ее структуры, специальных знаний и определенного опыта. СПИСОК ЛИТЕРАТУРЫ Бахвалов Н.С., Лапин А.В., Чижонков Е.В. Численные методы в задачах и упражнениях: учебное пособие. 2-е изд., перераб. и доп. − М.: БИНОМ. Лаборатория знаний, 2010. − 240 с. Игумнов Л.А., Литвинчук С.Ю., Белов А.А. ЭЛЕМЕНТЫ ЧИСЛЕННЫХ МЕТОДОВ РЕШЕНИЯ СИСТЕМ ЛИНЕЙНЫХ АЛГЕБРАИЧЕСКИХ УРАВНЕНИЙ: Учебно-методическое пособие. – Нижний Новгород: Нижегородский университет, 2010. – 24 с. Ильин В.А., Позняк Э.Г. Линейная алгебра: Учебник для вузов. – 6-е изд., стер. – М.: ФИЗМАТЛИТ, 2004 Курсовая работа. Подготовка, оформление, защита: Метод. рекомендации для самостоятельной работы студентов. Направления 44.03.01, 44.03.05 «Педагогическое образование». Профили «Математика», «Математика и Информатика» / сост. М.С. Ананьева. – Перм. гос. гуманит.-пед. ун-т. – Пермь, 2013. – 61 с. Лаборатория прикладной математики. Метод простых итераций для решения линейных систем [Электронный ресурс]. – Режим доступа: http://www.fm.cdml.ru/LabMotor/newdoc/Gauss.pdf. Осиновская, И.В. Численные методы решения алгебраических уравнений и их систем [Электронный ресурс]: электрон, учеб. пособие / И. В. Осиновская, А. Г. Шляпугин, Я. А. Ерисов; Минобрнауки России, Самар, гос. аэрокосм, ун-т им. С. П. Королева (нац. исслед. ун-т). Самарский А.А., Гулин А.В. Численные методы: Учеб. Пособие для вузов. – М.:Наука. Гл.ред физ.-мат. Лит-ры, 1989. – 432с. Теория и реализация задач вычислительной математики в пакете MathСad: учебное пособие / сост. А.И.Кочегуров, Е.А. Кочегурова; Томский политехнический университет. – Томск: Изд-во Томского политехнического университета, 2013. – 135 с. Турчак Л.И. Основы численных методов / Л.И. Турчак, П.В. Плотников. - М.: ФИЗМАТЛИТ, 2002. - 304 с. Фаддеев Д.К. Вычислительные методы линйеной алгебры / Фаддеев Д.К., Фаддеева В.Н. – 3-е изд., стереотип.-СПб.: Лань, 2002. – 733 с. Формалеев В.Ф., Ревизников Д.Л. Численные методы. – М.: ФИЗМАТЛИТ, 2004, 400 с. Численные методы в примерах и задачах: Учеб.пособие/В.И. Киреев, А.В.Пантелеев. – 3-е изд. стер.-М.: Высш.шк., 2008. – 480 с. Шахов Ю.Н., Деза Е.И. Численные методы: Учебное пособие. Изд.2-е, испр. и доп. − М.: Книжный дом «ЛИБРИКОМ», 2010. − 248 с | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||