Курсовая надежность. Курсовая работа По дисциплине Надёжность и техническая диагностика сложных систем
 Скачать 0.96 Mb. Скачать 0.96 Mb.
|
Исследование зависимости GR(t, n)Формула 2.6, представленная выше, является точной. Помимо нее существует приближенная 2.8: 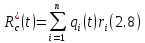 Их отношение имеет следующий вид 2.9: 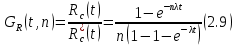 Рассмотрим предельные соотношения при различных значениях n. При n =8: 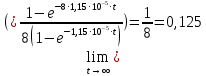 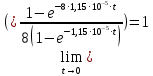 ъПри n = 24: 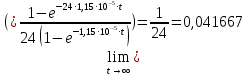 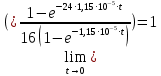 При n = 40: 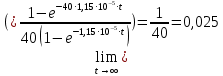 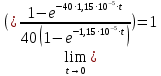 В таблице 13 представлены результаты вычислений зависимости GR(t, n). Таблица 13, результаты вычислений зависимости GR(t, n)
…….
По результатам вычислений был построен график зависимости GR(t, n) (рис.33). 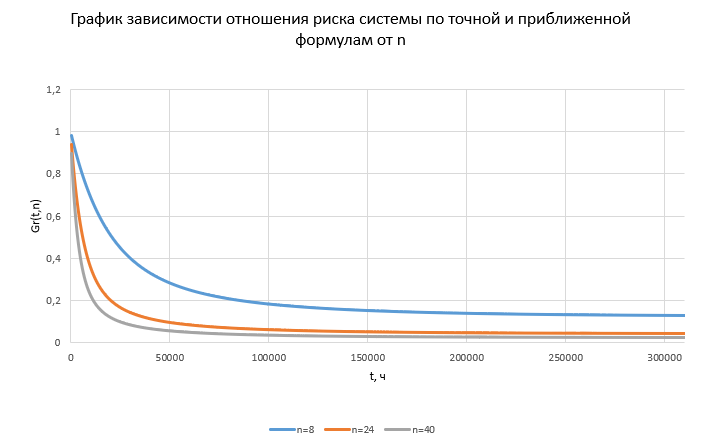 Рисунок 33, график зависимости график зависимости GR(t, n) Вычисление критического времени работыСуммарное время работы T = 3800 ч. Тогда из формулы 2.6 можно вывести формулу, определяющую критическое время работы системы: 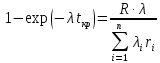 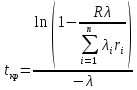 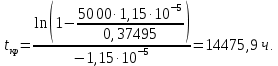 Следовательно, среднее время безотказной работы T1 = 10869,5652 ч. не превышает критического значения, что свидетельствует о том, что риск системы не превышает допустимых значений. Вывод по третьему заданиюВ ходе выполнения задания были определены основные показатели надежности: ВБР при t = T и при t = T1 P(T) = 0,705, P(T1) = 0,3679 и среднее время безотказной работы T1 = 10869,5652 ч. Риски системы при t = T и при t = T1 составили соответственно 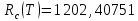 и и 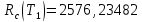 . Значения риска системы не превысили допустимого значения R = 5000 у.е., кроме того, среднее время безотказной работы T1 = 10869,5652 ч. не превышает критического значения, что свидетельствует о надежности рассматриваемой системы. . Значения риска системы не превысили допустимого значения R = 5000 у.е., кроме того, среднее время безотказной работы T1 = 10869,5652 ч. не превышает критического значения, что свидетельствует о надежности рассматриваемой системы. Анализ графика риска системы показал рост рисков с течением времени и при увеличении числа элементов. Функция GR(t, n) является убывающей, при увеличении количества элементов и с течением времени растет погрешность приближенной формулы 2.7. |
