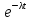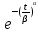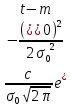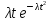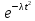На этом этапе были рассчитаны математическое ожидание mи среднее квадратическое отклонение σ0 по формулам 1.1 – 1.5 соответственно.
Экспоненциальный закон распределения:
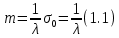
Гамма – распределение:
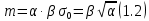
Усеченное нормальное распределение:
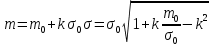 (1.3) (1.3)
где:
 ; ; 
Релея:
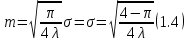
Вейбула:
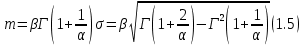
Ниже приведены расчеты начальных моментов распределения:
Релея:
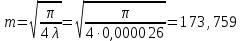
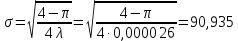
Экспоненциальное:
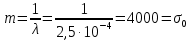
Гамма:
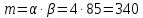
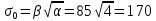
Усеченный нормальный:
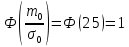


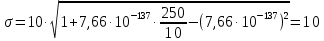
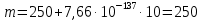
Вейбул:
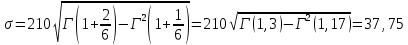
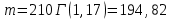
Расчет ВБР
На этом этапе для каждого элемента была рассчитана ВБР по формулам таблицы 1. Согласно заданию, количество членов в ряде значений t должно быть не менее 100, в связи с чем был выбран шаг интервала h = 3. Ниже представлены расчеты ВБР для каждого из 5 элементов и системы в целом при минимальных t = 0 ч и максимальных t = 300 ч значениях t. Результаты вычисления ВБР каждого элемента при каждом t представлены в таблице 2.
Таблица 1, формулы вычисления ВБР и плотности распределения времени БР при заданных законах распределения
Распределение
|
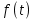
|
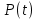
|
Г( ) )
|
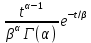
|

|
Exp(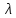 ) )
|

|
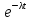
|
W( ) )
|

|
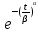
|
TN(
|
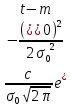
|

|
R(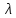 ) )
|
2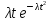
|
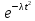
|
Распределение Релея:
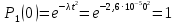
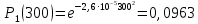
Экспоненциальный закон распределения:
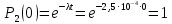
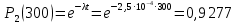
Гамма – распределение:
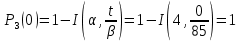
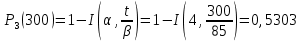
Нормальное усеченное распределение:

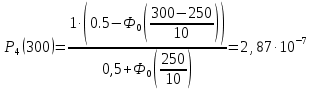
Распределение Вейбула

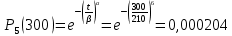
Поскольку рассматриваемая система представляет собой последовательно соединенные элементы, ВБР системы будет определяться по формуле 1.6:
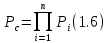
ВБР системы в целом при t = 0:
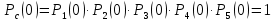
ВБР системы в целом при t = 300:
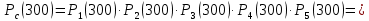
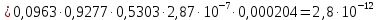
Таблица 2, результаты вычисления ВБР каждого элемента и системы в целом
t, час
|
R
|
exp
|
Г
|
TN
|
W
|
системы
|
|
P1(t)
|
P2(t)
|
P3(t)
|
P4(t)
|
P5(t)
|
Pc(t)
|
0
|
1
|
1
|
1
|
1
|
1
|
1
|
3
|
0,999766
|
0,99925
|
1
|
1
|
1
|
0,999016
|
6
|
0,999064
|
0,998501
|
0,999999
|
1
|
1
|
0,997566
|
9
|
0,997896
|
0,997753
|
0,999995
|
1
|
1
|
0,995649
|
12
|
0,996263
|
0,997004
|
0,999985
|
1
|
1
|
0,993264
|
15
|
0,994167
|
0,996257
|
0,999965
|
1
|
1
|
0,990411
|
18
|
0,991611
|
0,99551
|
0,999929
|
1
|
1
|
0,987089
|
21
|
0,988599
|
0,994764
|
0,999872
|
1
|
0,999999
|
0,983297
|
24
|
0,985136
|
0,994018
|
0,999788
|
1
|
0,999998
|
0,979033
|
27
|
0,981224
|
0,993273
|
0,999671
|
1
|
0,999995
|
0,974298
|
30
|
0,976872
|
0,992528
|
0,999512
|
1
|
0,999992
|
0,969091
|
33
|
0,972083
|
0,991784
|
0,999305
|
1
|
0,999985
|
0,963412
|
36
|
0,966865
|
0,99104
|
0,999042
|
1
|
0,999975
|
0,957261
|
39
|
0,961226
|
0,990297
|
0,998717
|
1
|
0,999959
|
0,950639
|
42
|
0,955172
|
0,989555
|
0,998322
|
1
|
0,999936
|
0,943548
|
45
|
0,948712
|
0,988813
|
0,997849
|
1
|
0,999903
|
0,93599
|
48
|
0,941855
|
0,988072
|
0,997291
|
1
|
0,999857
|
0,927967
|
51
|
0,93461
|
0,987331
|
0,996642
|
1
|
0,999795
|
0,919482
|
54
|
0,926987
|
0,986591
|
0,995894
|
1
|
0,999711
|
0,910538
|
57
|
0,918996
|
0,985851
|
0,995042
|
1
|
0,9996
|
0,90114
|
60
|
0,910647
|
0,985112
|
0,994078
|
1
|
0,999456
|
0,891292
|
…
240
|
0,223666
|
0,941765
|
0,686698
|
0,841345
|
0,107724
|
0,01311
|
243
|
0,215397
|
0,941058
|
0,678825
|
0,758036
|
0,090663
|
0,009457
|
246
|
0,207336
|
0,940353
|
0,670939
|
0,655422
|
0,07547
|
0,006471
|
249
|
0,199483
|
0,939648
|
0,663042
|
0,539828
|
0,062104
|
0,004167
|
252
|
0,191838
|
0,938943
|
0,655139
|
0,42074
|
0,05049
|
0,002507
|
255
|
0,1844
|
0,93824
|
0,647232
|
0,308538
|
0,04053
|
0,0014
|
258
|
0,177167
|
0,937536
|
0,639325
|
0,211855
|
0,032104
|
0,000722
|
261
|
0,170138
|
0,936833
|
0,631421
|
0,135666
|
0,025078
|
0,000342
|
264
|
0,163311
|
0,936131
|
0,623524
|
0,080757
|
0,019305
|
0,000149
|
267
|
0,156686
|
0,935429
|
0,615637
|
0,044565
|
0,014636
|
5,89E-05
|
270
|
0,150258
|
0,934728
|
0,607761
|
0,02275
|
0,01092
|
2,12E-05
|
273
|
0,144027
|
0,934027
|
0,599902
|
0,010724
|
0,008012
|
6,93E-06
|
276
|
0,13799
|
0,933327
|
0,59206
|
0,004661
|
0,005777
|
2,05E-06
|
279
|
0,132144
|
0,932627
|
0,58424
|
0,001866
|
0,00409
|
5,49E-07
|
282
|
0,126486
|
0,931928
|
0,576443
|
0,000687
|
0,00284
|
1,33E-07
|
285
|
0,121014
|
0,931229
|
0,568672
|
0,000233
|
0,001934
|
2,88E-08
|
288
|
0,115724
|
0,930531
|
0,560931
|
7,23E-05
|
0,00129
|
5,64E-09
|
291
|
0,110614
|
0,929833
|
0,55322
|
2,07E-05
|
0,000842
|
9,89E-10
|
294
|
0,10568
|
0,929136
|
0,545544
|
5,41E-06
|
0,000537
|
1,56E-10
|
297
|
0,100919
|
0,92844
|
0,537903
|
1,3E-06
|
0,000335
|
2,19E-11
|
300
|
0,096328
|
0,927743
|
0,5303
|
2,87E-07
|
0,000203
|
2,76E-12
|
По данным, полученным в ходе вычислений ВБР был построен график зависимости ВБР от времени (рис.6).

Рисунок 6, график ВБР для 5 элементов системы и системы в целом
|
 Скачать 0.96 Mb.
Скачать 0.96 Mb.
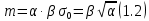
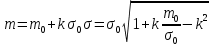 (1.3)
(1.3) ;
; 
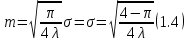
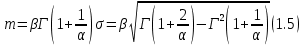
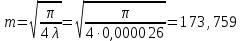
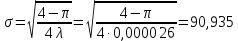
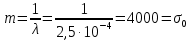
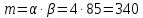
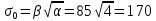
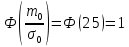


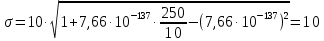
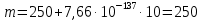
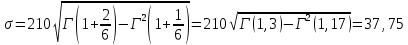
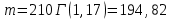
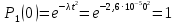
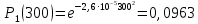
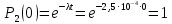
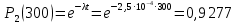
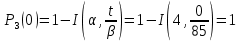
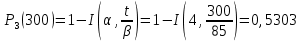

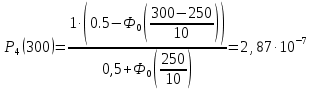

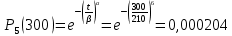
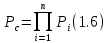
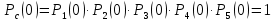
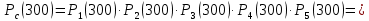
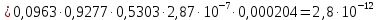


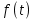
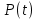
 )
)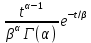

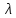 )
)