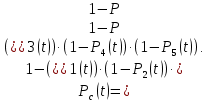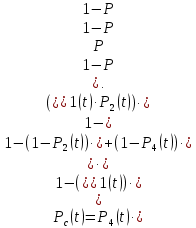Надежность системы для параллельного соединения и когда элемент с минимальным значением надежности подключен в систему по схеме мостового резерва
При параллельном соединении воспользуемся формулой:
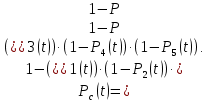
Соединение, когда элемент с минимальным значением надежности подключен в систему по схеме мостового резерва.
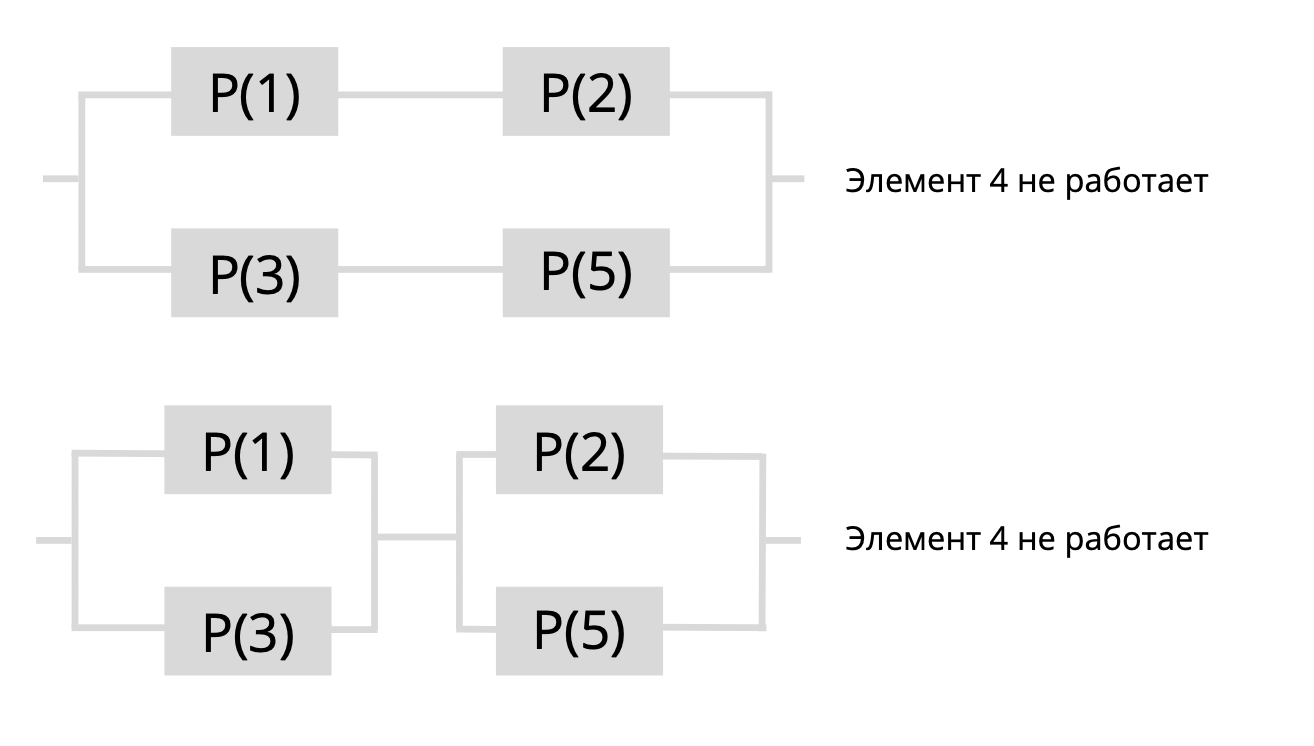
Элемент с минимальным значением надежности – это элемент №4 с экспоненциальным распределение, запишем формулу для этого случая:
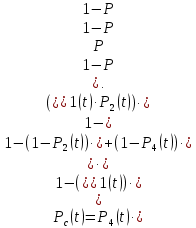
Результаты вычислений отобразим в таблице:
t
|
P паралл
|
P мост
|
0
|
1
|
1
|
3
|
1
|
1
|
6
|
1
|
1
|
9
|
1
|
1
|
12
|
1
|
1
|
15
|
1
|
0,999999998
|
18
|
1
|
0,999999994
|
21
|
1
|
0,999999981
|
24
|
1
|
0,999999948
|
27
|
1
|
0,999999874
|
30
|
1
|
0,999999719
|
33
|
1
|
0,99999942
|
36
|
1
|
0,999998875
|
39
|
1
|
0,999997927
|
42
|
1
|
0,999996345
|
45
|
1
|
0,9999938
|
48
|
1
|
0,99998983
|
51
|
1
|
0,999983804
|
54
|
1
|
0,999974876
|
57
|
1
|
0,999961934
|
60
|
1
|
0,999943532
|
63
|
1
|
0,999917827
|
66
|
1
|
0,999882491
|
69
|
1
|
0,99983462
|
72
|
1
|
0,999770634
|
75
|
1
|
0,999686159
|
78
|
1
|
0,999575906
|
81
|
1
|
0,999433526
|
84
|
1
|
0,999251472
|
87
|
1
|
0,99902083
|
90
|
1
|
0,998731156
|
93
|
1
|
0,998370294
|
96
|
1
|
0,997924193
|
99
|
1
|
0,997376715
|
102
|
1
|
0,996709439
|
105
|
1
|
0,995901471
|
108
|
1
|
0,994929248
|
111
|
1
|
0,993766361
|
114
|
1
|
0,992383383
|
117
|
1
|
0,990747719
|
120
|
1
|
0,988823484
|
123
|
1
|
0,986571415
|
126
|
1
|
0,98394882
|
129
|
1
|
0,980909586
|
132
|
1
|
0,977404246
|
135
|
1
|
0,973380123
|
138
|
1
|
0,968781549
|
141
|
1
|
0,963550196
|
144
|
1
|
0,9576255
|
147
|
1
|
0,950945217
|
150
|
1
|
0,943446094
|
153
|
1
|
0,935064692
|
156
|
1
|
0,925738342
|
159
|
1
|
0,915406249
|
162
|
1
|
0,904010739
|
165
|
1
|
0,891498645
|
168
|
1
|
0,87782281
|
171
|
1
|
0,862943702
|
174
|
1
|
0,84683109
|
177
|
1
|
0,829465772
|
180
|
1
|
0,81084128
|
183
|
1
|
0,790965528
|
186
|
1
|
0,769862332
|
189
|
1
|
0,747572724
|
192
|
1
|
0,724156001
|
195
|
1
|
0,699690406
|
198
|
1
|
0,674273383
|
201
|
0,999999998
|
0,648021305
|
204
|
0,999999991
|
0,62106858
|
207
|
0,99999996
|
0,593565958
|
210
|
0,999999835
|
0,565677678
|
213
|
0,999999374
|
0,537576679
|
216
|
0,99999783
|
0,509436387
|
219
|
0,999993117
|
0,481416881
|
222
|
0,999980017
|
0,453643323
|
225
|
0,999946841
|
0,426177051
|
228
|
0,99987028
|
0,398986128
|
231
|
0,999709218
|
0,371931389
|
234
|
0,999400223
|
0,344790594
|
237
|
0,998859334
|
0,317337766
|
240
|
0,997994823
|
0,28947101
|
243
|
0,996731957
|
0,261346709
|
246
|
0,995043633
|
0,233453143
|
249
|
0,992973918
|
0,206566931
|
252
|
0,990640601
|
0,181586319
|
255
|
0,988210987
|
0,159300197
|
258
|
0,985858638
|
0,14018858
|
261
|
0,983719189
|
0,124333648
|
264
|
0,981863393
|
0,111462022
|
267
|
0,980295454
|
0,101077811
|
270
|
0,97897175
|
0,0926173
|
273
|
0,97782737
|
0,085567829
|
276
|
0,97679853
|
0,079527246
|
279
|
0,975835026
|
0,074211656
|
282
|
0,974903213
|
0,069433889
|
285
|
0,973983287
|
0,065073895
|
288
|
0,973064786
|
0,061053465
|
291
|
0,972142626
|
0,057319132
|
294
|
0,971214471
|
0,053832184
|
297
|
0,970279277
|
0,050563315
|
300
|
0,96933659
|
0,047489746
|
Отобразим это графически:
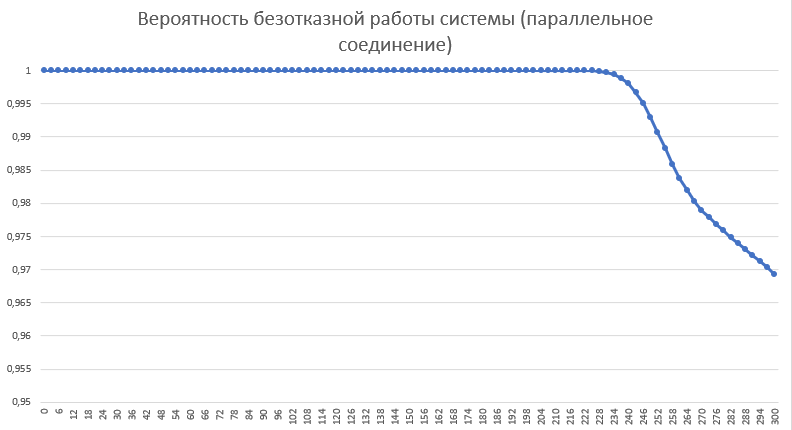
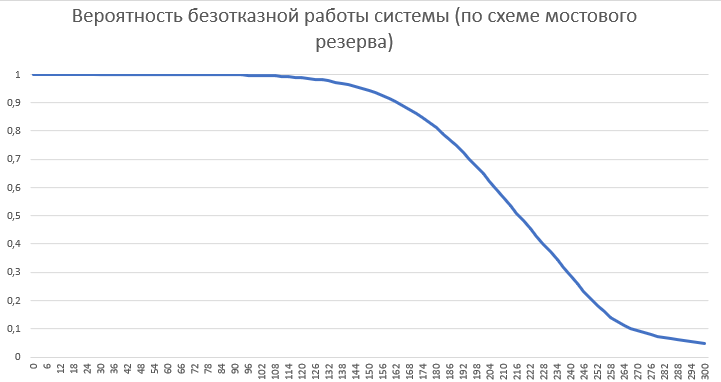
|
 Скачать 0.96 Mb.
Скачать 0.96 Mb.