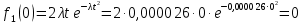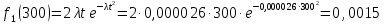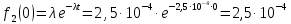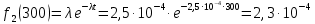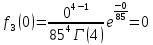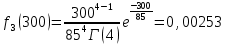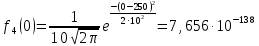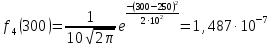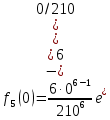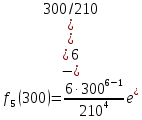Расчет плотности распределения времени БР
Распределение Релея:
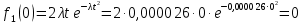
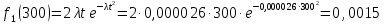
Экспоненциальное распределение:
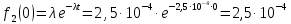
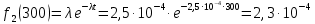
Гамма распределение:
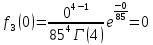
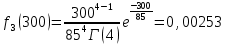
Усеченное нормальное распределение:
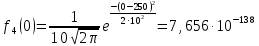
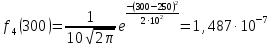
Распределение Вейбула:
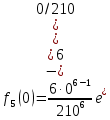
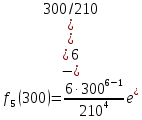
Результаты вычисления плотности распределения каждого элемента при каждом t представлены в таблице 3.
Таблица 3, результаты вычисления плотности распределения каждого элемента
t,ч
|
R
|
exp
|
Г
|
TN
|
W
|
fc
|
0
|
0
|
0,00025
|
0
|
7,6559E-138
|
0
|
0,00025
|
3
|
0,000156
|
0,00025
|
8,32164E-08
|
1,3233E-134
|
1,69997E-11
|
0,000406
|
6
|
0,000312
|
0,00025
|
6,42644E-07
|
2,0904E-131
|
5,43991E-10
|
0,000561
|
9
|
0,000467
|
0,000249
|
2,09371E-06
|
3,0181E-128
|
4,13093E-09
|
0,000717
|
12
|
0,000622
|
0,000249
|
4,79076E-06
|
3,9823E-125
|
1,74077E-08
|
0,000873
|
15
|
0,000775
|
0,000249
|
9,03247E-06
|
4,8024E-122
|
5,31241E-08
|
0,001029
|
18
|
0,000928
|
0,000249
|
1,50668E-05
|
5,2928E-119
|
1,3219E-07
|
0,001186
|
21
|
0,00108
|
0,000249
|
2,30959E-05
|
5,3313E-116
|
2,85714E-07
|
0,001343
|
24
|
0,001229
|
0,000249
|
3,32799E-05
|
4,9079E-113
|
5,57046E-07
|
0,0015
|
27
|
0,001378
|
0,000248
|
4,57417E-05
|
4,1292E-110
|
1,00381E-06
|
0,001657
|
30
|
0,001524
|
0,000248
|
6,05698E-05
|
3,1751E-107
|
1,69996E-06
|
0,001814
|
33
|
0,001668
|
0,000248
|
7,78227E-05
|
2,2313E-104
|
2,73778E-06
|
0,001972
|
36
|
0,00181
|
0,000248
|
9,75313E-05
|
1,4331E-101
|
4,22997E-06
|
0,002129
|
39
|
0,001949
|
0,000248
|
0,000119702
|
8,412E-99
|
6,31162E-06
|
0,002285
|
42
|
0,002086
|
0,000247
|
0,000144321
|
4,51271E-96
|
9,14227E-06
|
0,002442
|
45
|
0,00222
|
0,000247
|
0,000171352
|
2,21255E-93
|
1,29079E-05
|
0,002597
|
48
|
0,002351
|
0,000247
|
0,000200747
|
9,91425E-91
|
1,7823E-05
|
0,002752
|
51
|
0,002479
|
0,000247
|
0,000232438
|
4,06014E-88
|
2,41322E-05
|
0,002905
|
54
|
0,002603
|
0,000247
|
0,000266348
|
1,51962E-85
|
3,21128E-05
|
0,003057
|
57
|
0,002724
|
0,000246
|
0,000302388
|
5,1981E-83
|
4,20762E-05
|
0,003208
|
60
|
0,002841
|
0,000246
|
0,00034046
|
1,62505E-80
|
5,43695E-05
|
0,003357
|
…
240
|
0,002791
|
0,000235
|
0,002621582
|
0,024203208
|
0,006000705
|
0,001324
|
243
|
0,002722
|
0,000235
|
0,002626761
|
0,031233311
|
0,005373961
|
0,001109
|
246
|
0,002652
|
0,000235
|
0,002630747
|
0,036836352
|
0,004756505
|
0,000881
|
249
|
0,002583
|
0,000235
|
0,002633563
|
0,03970532
|
0,004158634
|
0,000657
|
252
|
0,002514
|
0,000235
|
0,002635234
|
0,039114185
|
0,003589565
|
0,000455
|
255
|
0,002445
|
0,000235
|
0,002635786
|
0,03521546
|
0,003057108
|
0,00029
|
258
|
0,002377
|
0,000234
|
0,002635243
|
0,028976501
|
0,002567423
|
0,000169
|
261
|
0,002309
|
0,000234
|
0,002633632
|
0,021790742
|
0,002124868
|
9,02E-05
|
264
|
0,002242
|
0,000234
|
0,002630978
|
0,014976543
|
0,001731946
|
4,36E-05
|
267
|
0,002175
|
0,000234
|
0,002627309
|
0,009407293
|
0,001389358
|
1,91E-05
|
270
|
0,00211
|
0,000234
|
0,002622652
|
0,005400466
|
0,001096151
|
7,56E-06
|
273
|
0,002045
|
0,000234
|
0,002617034
|
0,002833422
|
0,000849948
|
2,7E-06
|
276
|
0,00198
|
0,000233
|
0,002610481
|
0,001358641
|
0,000647227
|
8,68E-07
|
279
|
0,001917
|
0,000233
|
0,002603022
|
0,000595404
|
0,000483648
|
2,51E-07
|
282
|
0,001855
|
0,000233
|
0,002594685
|
0,000238469
|
0,000354378
|
6,51E-08
|
285
|
0,001793
|
0,000233
|
0,002585495
|
8,72904E-05
|
0,000254396
|
1,52E-08
|
288
|
0,001733
|
0,000233
|
0,002575483
|
2,92021E-05
|
0,000178769
|
3,17E-09
|
291
|
0,001674
|
0,000232
|
0,002564673
|
8,92843E-06
|
0,000122866
|
5,92E-10
|
294
|
0,001616
|
0,000232
|
0,002553096
|
2,49488E-06
|
8,25156E-05
|
9,88E-11
|
297
|
0,001559
|
0,000232
|
0,002540776
|
6,37144E-07
|
5,41001E-05
|
1,47E-11
|
300
|
0,001503
|
0,000232
|
0,002527742
|
1,4871E-07
|
3,45939E-05
|
1,96E-12
|
 По данным, полученным в ходе вычислений плотности распределения был построен график зависимости плотности распределения от времени (рис.7).
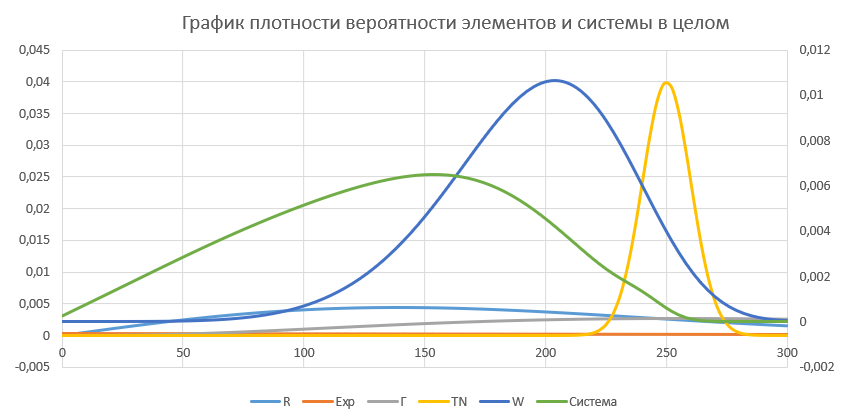
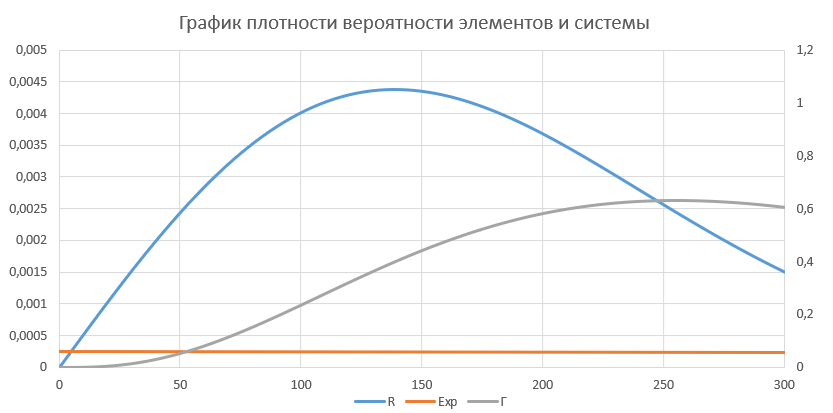
Рис. 7, Графики плотности вероятности элементов системы и системы в целом
|
Скачать 0.96 Mb.