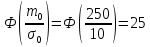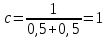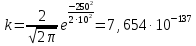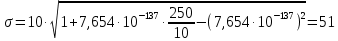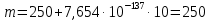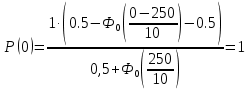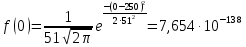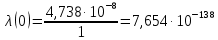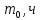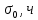Задание №2
Вариант
|
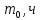
|
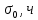
|
4
|
250
|
10
|
Цель задания: определить все показатели надежности резервированной системы с параметрами 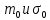 , значения которых в соответствии с вариантом представленны выше. Результаты представить в виде таблиц и графиков, принять m = 0, 1, 2, 3. , значения которых в соответствии с вариантом представленны выше. Результаты представить в виде таблиц и графиков, принять m = 0, 1, 2, 3.
Ход выполнения
На первом этапе, по исходным данным были построены графики функции и плотности распределения (рис.16).
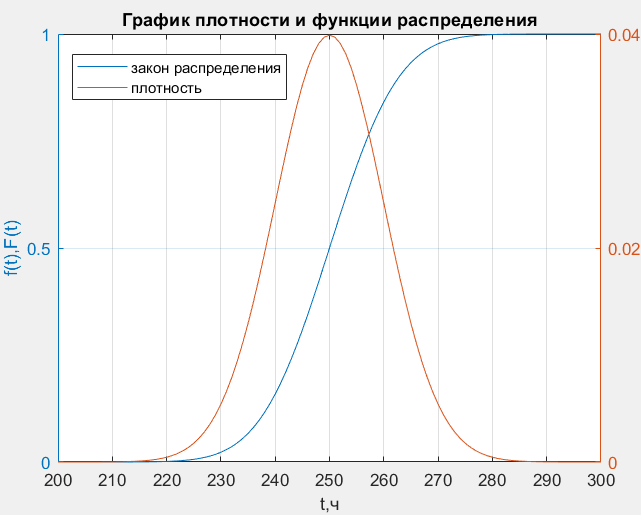
Рисунок 16, график функции и плотности распределения (нормальный усеченный закон распределения)
Расчет начальных моментов распределения
На этом этапе были рассчитаны математическое ожидание mи среднее квадратическое отклонение σ0 по формуле 1.3.
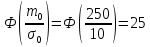
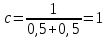
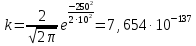
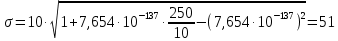
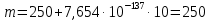
Расчет ВБР, плотности распределения и интенсивности отказов системы
ВБР при t = 0:
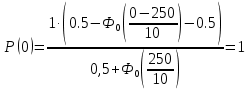
Плотность распределения при t = 0:
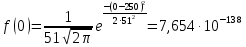
Интенсивность отказов при t = 0:
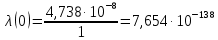
Результаты вычисления ВБР, плотности распределения и интенсивности отказов при каждом значении t представлены в таблице 8.
Таблица 8, результаты вычисления ВБР, плотности распределения и интенсивности отказов
t, ч.
|
P(t)
|
f(t)
|
λ(t)
|
0
|
1
|
7,654E-138
|
7,6539E-138
|
3
|
1
|
1,323E-134
|
1,323E-134
|
6
|
1
|
2,09E-131
|
2,0899E-131
|
9
|
1
|
3,017E-128
|
3,0173E-128
|
12
|
1
|
3,981E-125
|
3,9813E-125
|
15
|
1
|
4,801E-122
|
4,8012E-122
|
18
|
1
|
5,292E-119
|
5,2915E-119
|
21
|
1
|
5,33E-116
|
5,33E-116
|
24
|
1
|
4,907E-113
|
4,9067E-113
|
27
|
1
|
4,128E-110
|
4,1282E-110
|
30
|
1
|
3,174E-107
|
3,1743E-107
|
33
|
1
|
2,231E-104
|
2,2307E-104
|
36
|
1
|
1,433E-101
|
1,4327E-101
|
39
|
1
|
8,41E-99
|
8,4098E-99
|
42
|
1
|
4,5116E-96
|
4,51157E-96
|
45
|
1
|
2,212E-93
|
2,21198E-93
|
48
|
1
|
9,9117E-91
|
9,91174E-91
|
51
|
1
|
4,0591E-88
|
4,05911E-88
|
54
|
1
|
1,5192E-85
|
1,51924E-85
|
57
|
1
|
5,1968E-83
|
5,19678E-83
|
60
|
1
|
1,6246E-80
|
1,62464E-80
|
…
240
|
0,841344746
|
0,02419707
|
0,028759996
|
243
|
0,758036348
|
0,03122539
|
0,041192473
|
246
|
0,655421742
|
0,03682701
|
0,056188267
|
249
|
0,539827837
|
0,03969525
|
0,073533171
|
252
|
0,420740291
|
0,03910427
|
0,09294158
|
255
|
0,308537539
|
0,03520653
|
0,114107771
|
258
|
0,211855399
|
0,02896915
|
0,136740219
|
261
|
0,135666061
|
0,02178522
|
0,160579708
|
264
|
0,080756659
|
0,01497275
|
0,18540571
|
267
|
0,044565463
|
0,00940491
|
0,211035781
|
270
|
0,022750132
|
0,0053991
|
0,23732154
|
273
|
0,01072411
|
0,0028327
|
0,264143469
|
276
|
0,004661188
|
0,0013583
|
0,291405719
|
279
|
0,001865813
|
0,00059525
|
0,319031496
|
282
|
0,000687138
|
0,00023841
|
0,346959168
|
285
|
0,000232629
|
8,7268E-05
|
0,375139106
|
288
|
7,2348E-05
|
2,9195E-05
|
0,403531172
|
291
|
2,06575E-05
|
8,9262E-06
|
0,432102735
|
294
|
5,41254E-06
|
2,4942E-06
|
0,460827115
|
297
|
1,30081E-06
|
6,3698E-07
|
0,489682374
|
300
|
2,86652E-07
|
1,4867E-07
|
0,518650368
|
|
 Скачать 0.96 Mb.
Скачать 0.96 Mb.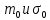 , значения которых в соответствии с вариантом представленны выше. Результаты представить в виде таблиц и графиков, принять m = 0, 1, 2, 3.
, значения которых в соответствии с вариантом представленны выше. Результаты представить в виде таблиц и графиков, принять m = 0, 1, 2, 3.