курсовой проект СХЕМНЫЕ ФУНКЦИИ И ЧАСТОТНЫЕ ХАРАКТЕРИСТИКИ ЛИНЕЙНЫХ ЭЛЕКТРИЧЕСКИХ ЦЕПЕЙ. курсовой проект СХЕМНЫЕ ФУНКЦИИ И ЧАСТОТНЫЕ ХАРАКТЕРИСТИКИ ЛИНЕЙ. Курсовая работа по дисциплине Теория электрических цепей

• Название: Курсовая работа по дисциплине Теория электрических цепей
• Анкор: курсовой проект СХЕМНЫЕ ФУНКЦИИ И ЧАСТОТНЫЕ ХАРАКТЕРИСТИКИ ЛИНЕЙНЫХ ЭЛЕКТРИЧЕСКИХ ЦЕПЕЙ
• Дата: 21.11.2022
• Размер: 0.71 Mb.
• Имя файла: курсовой проект СХЕМНЫЕ ФУНКЦИИ И ЧАСТОТНЫЕ ХАРАКТЕРИСТИКИ ЛИНЕЙ.docx
• Тип: Курсовая; #803214
• страница: 7 из 10

Расчет резонансных частот и резонансных сопротивлений

Для получения комплексной входной функции избирательной нагрузки необходимо произвести формальную замену в операторной входной
функции (2.4) p=j.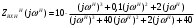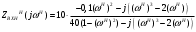

,

. (2.12)

АЧХ входной функции избирательной нагрузки описывается выражением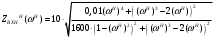

. (2.13)

ФЧХ входной функции избирательной нагрузки описывается выражениями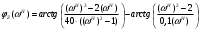

(2.14)

Графики АЧХ и ФЧХ комплексной входной функции нагрузки, построенные по (2.13) (2.14), приведены на рисунках 2.10 и 2.11.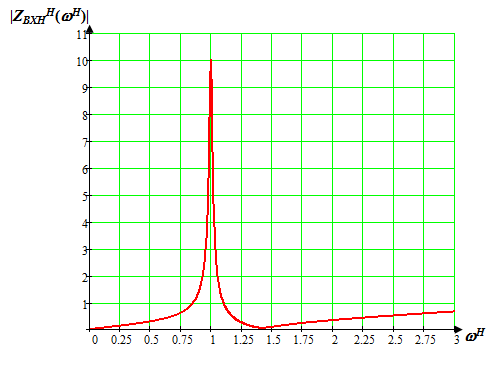



Рисунок 2.10 – График АЧХ входной функции нагрузки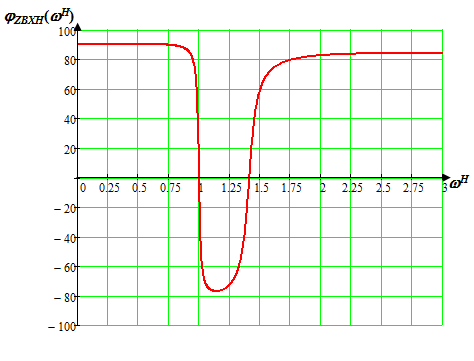


Рисунок 2.11 – График ФЧХ входной функции нагрузки
Так как при резонансе сопротивление контура становится чисто активным, для определения резонансных частот приравняем ФЧХ входной функции нагрузки к нулю.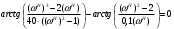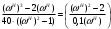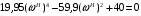

;

;

. (2.15)

Корни уравнения (2.15):

^Н_1,2=1; ^Н_3,4=1,41.

Определили две резонансных частоты: ^Н_Р1=1 и ^Н_Р2=1,41.

Определим резонансные сопротивления, подставив значения резонансных частот в (2.13).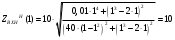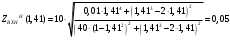

,

.

Нормированные значения резонансных сопротивлений: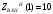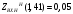

;

.

Определим ненормированные значения резонансных частот и сопротивлений.

f_р1=7,051=7,05 МГц,

R_P1=30010=3000 Ом=3 кОм,

f_р2=7,051,41=10 МГц,

R_P2=3000,05=15 Ом.

Результаты расчета совпадают с результатами, полученными при схемном анализе.

9. Определение полосы пропускания цепи

Полосу пропускания цепи обычно оценивают как диапазон частот, в пределах которого АЧХ превышает уровень 0,707 максимального значения.

Полоса пропускания для двухполюсников определяется по входной функции нагрузки [1].

Для определения полосы пропускания, приравняем модуль нормированной входной функции цепи к значению, равному 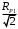и определим значения ^Н.

,

,

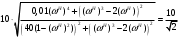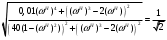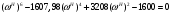. (2.16)

Корни уравнения (2.16):

^Н_1,2=0,987;  ^Н_3,4=1,012;  ^Н_5,6=40,075.

Граничными частотами являются корни:

 ^Н₁=0,987;  ^Н₃=1,012.

Нижняя частота полосы пропускания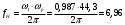

МГц.

Верхняя частота полосы пропускания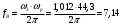

МГц.

Ширина полосы пропускания по уровню 3 дБ

2f=f_Вf_Н =7,146,96=0,18 МГц.

3. Исследование схемы транзистора с обобщенной нагрузкой

   1. Вывод операторных выражений входной и передаточной функций на основе метода узловых потенциалов

Схема модели транзистора с обобщенной нагрузкой приведена на рисунке 3.1.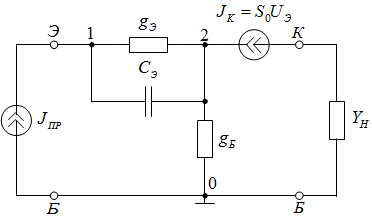



Рисунок 3.1 – Схема модели транзистора с обобщенной нагрузкой
Определение схемных функций транзистора с обобщенной нагрузкой проведем с использованием метода узловых потенциалов (МУП).

Для реализации МУП на вход подключим пробный источник J_пр
(рисунок 3.1).

Заменим сопротивления элементов их проводимостями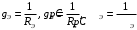

.

Запишем систему уравнений для заданной схемы: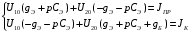



Выразим зависимый источник через узловые напряжения: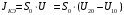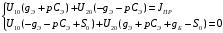

,

.

Для определения схемных функций систему представим в матричной форме: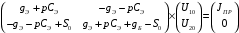



По правилу Крамера: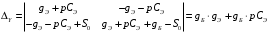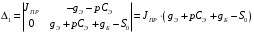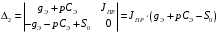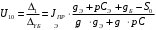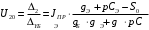

,

,

,

,

.

Операторное выражение входной функции: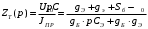

.

Операторное выражение передаточной функции: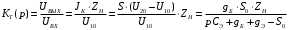

.