курсовой проект СХЕМНЫЕ ФУНКЦИИ И ЧАСТОТНЫЕ ХАРАКТЕРИСТИКИ ЛИНЕЙНЫХ ЭЛЕКТРИЧЕСКИХ ЦЕПЕЙ. курсовой проект СХЕМНЫЕ ФУНКЦИИ И ЧАСТОТНЫЕ ХАРАКТЕРИСТИКИ ЛИНЕЙ. Курсовая работа по дисциплине Теория электрических цепей
 Скачать 0.71 Mb. Скачать 0.71 Mb.
|
Вывод операторного выражения входной функции нагрузкиСхема цепи нагрузки приведена на рисунке 1.1. Так как значения индуктивностей L1=L2, индуктивное сопротивление в операторной форме примем равным pL1. Таким образом, операторные сопротивления реактивных элементов цепи нагрузки имеют вид 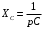 , , 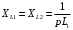 . .Входное сопротивление цепи нагрузки в операторной форме: 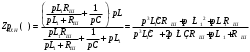 . .Операторное выражение входной функции избирательной нагрузки: 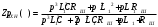 . (2.3) . (2.3)Проверка операторного выражения входной функции цепи нагрузкиПолученная входная функция нагрузки должна быть проверена разными способами: по размерности, на крайних частотах, на соответствие степеней полиномов порядку цепи, по соотношению максимальных степеней полиномов числителя и знаменателя функции. Проведем проверку размерности. Все слагаемые одного полинома должны иметь одинаковую размерность, а размерность функции в целом должна соответствовать ее физическому смыслу. Очевидно, что комплексное входное сопротивление имеет размерность сопротивления [2]. При проверке размерности учитываем, что 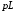 имеет размерность Ом, а имеет размерность Ом, а 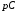 имеет размерность Ом1. имеет размерность Ом1.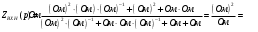 . .Проверка размерности подтверждает правильность операторного выражения входной функции нагрузки. Проверим соответствие модели входной функции на крайних частотах диапазона. 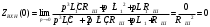 . .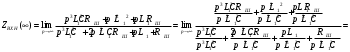 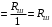 . .Результаты проверки на операторной функции на крайних частотах соответствуют эквивалентным моделям цепи на крайних частотах (рисунок 2.4). Проверим соответствие операторной входной функции цепи нагрузки порядку полиномов. Порядок полиномов определяется по формуле [1]: 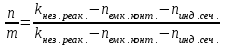 , ,где 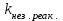 – количество независимых реактивностей в схеме; – количество независимых реактивностей в схеме;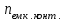 – количество емкостных контуров; – количество емкостных контуров;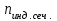 – количество индуктивных сечений. – количество индуктивных сечений.Емкостных контуров и индуктивных сечений в схеме нет. 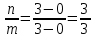 . .Порядки полиномов соответствуют схеме. Проверим соответствие модели входной функции условиям физической реализуемости. Так как присутствуют все степени р и все коэффициенты р одного знака (положительные), полином знаменателя является полиномом Гурвица. Степень числителя равна степени знаменателя. Условия физической реализуемости соблюдаются. Нормировка операторных функцийНормировку операторной входной функции произведем, подставив в выражение (2.3) нормированных значений L, C, RШ, приведенных в таблице 1.3. 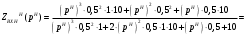 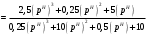 . .Выделим коэффициенты при максимальной степени р числителя и знаменателя. 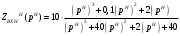 . (2.4) . (2.4)Определение нулей и полюсов входной функцииОпределим нули и полюса входной функции нагрузки как корни числителя и знаменателя полиномов выражения (2.4). Нули входной функции: р01,2=0,05±j1,413; р03=0. Полюса входной функции: рп1=40; рп2,3=0,012j1. Масштабный коэффициент Z0=10. Фаза масштабного коэффициента Z0=00. Карта нулей и полюсов входной функции нагрузки приведена на рисунке 2.7. 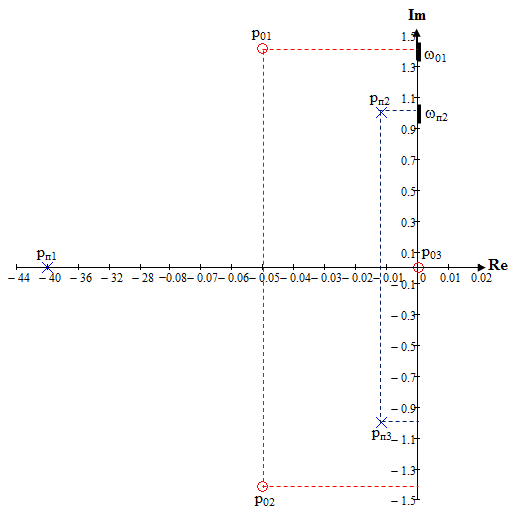 Рисунок 2.7 – Карта нулей и полюсов входной функции нагрузки |
