курсовой проект СХЕМНЫЕ ФУНКЦИИ И ЧАСТОТНЫЕ ХАРАКТЕРИСТИКИ ЛИНЕЙНЫХ ЭЛЕКТРИЧЕСКИХ ЦЕПЕЙ. курсовой проект СХЕМНЫЕ ФУНКЦИИ И ЧАСТОТНЫЕ ХАРАКТЕРИСТИКИ ЛИНЕЙ. Курсовая работа по дисциплине Теория электрических цепей
 Скачать 0.71 Mb. Скачать 0.71 Mb.
|
Исследование нагрузкиПредполагаемый на основе схемы характер АЧХ и ФЧХ входной и передаточной функцийЧисло независимых реактивностей в контуре равно трем, значит число возможных резонансов – два. В заданном избирательном двухполюснике возможен резонанс токов в контуре L1CL2 и резонанс напряжений в ветви L1C. Определим нормированную частоту резонанса токов РТ. 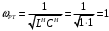 . .Определим нормированную частоту резонанса напряжений РН. 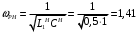 . .Цепь нагрузки представляет собой параллельный колебательный контур с разделенными индуктивностями с коэффициентом включения рL=0,5. На рисунке 2.1 приведены диаграммы сопротивлений двухполюсников, образованных параллельным соединением индуктивности L=L1+L2 и емкости С (кривые 1) и последовательным соединением индуктивности L1 и емкости С (кривая 2). При разделении индуктивности Lна L1 и L2 диаграмма сопротивлений двухполюсника примет вид, показанный на рисунке 2.2. График модуля реактивного сопротивления двухполюсника с разделенными индуктивностями приведен на рисунке 2.3. Такой характер будет иметь АЧХ входной функции двухполюсника нагрузки без учета влияния сопротивления RШ. 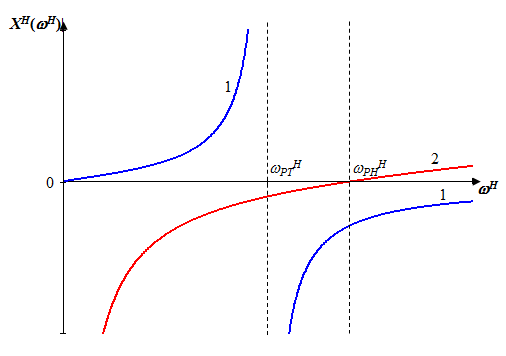 Рисунок 2.1 – Диаграммы сопротивлений двухполюсников 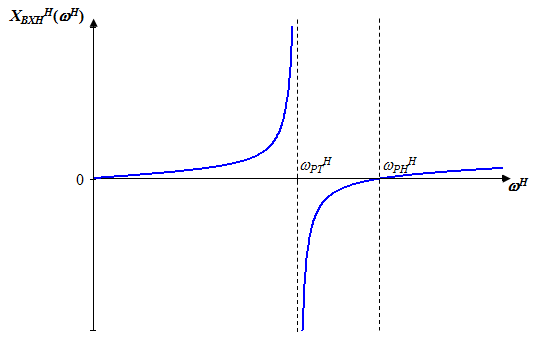 Рисунок 2.2 – Диаграмма сопротивлений двухполюсника после разделения индуктивностей 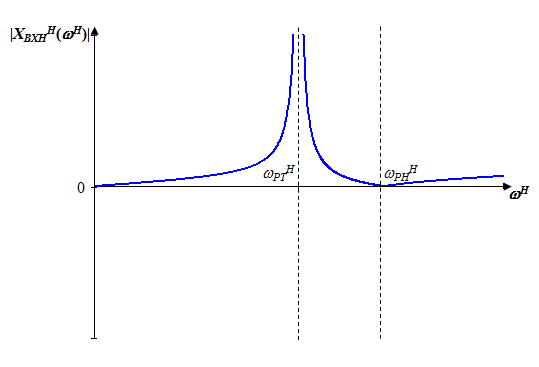 Рисунок 2.3 – График модуля реактивного сопротивления двухполюсника после разделения индуктивностей Для определения окончательного характера АЧХ входной функции нагрузки необходимо определить значения АЧХ в характерных точках. Эквивалентные модели цепи нагрузки на крайних частотах приведены на рисунке 2.4. 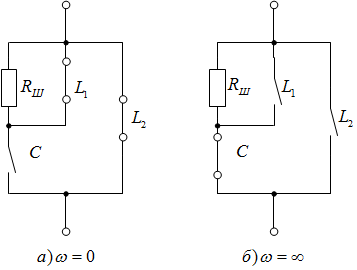 Рисунок 2.4 – Эквивалентные модели цепи нагрузки на крайних частотах Из рисунка 2.1 следует, что при =0 сопротивление двухполюсника нагрузки рано нулю из-за влияния индуктивности L2. При = сопротивление двухполюсника равно RШ. Определим нормированные резонансные сопротивления двухполюсника нагрузки. Сопротивление нагрузки при резонансе токов определим по формуле 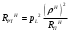 , (2.1) , (2.1)где RПН – нормированное сопротивление потерь контура. Нормированное сопротивление потерь контура определяется потерями, вносимыми сопротивлением RШ в индуктивность L1, и определяется по формуле 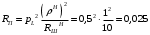 . .Подставив RП в (2.1), получим значение нормированного сопротивления нагрузки при резонансе токов. 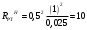 . .Сопротивление нагрузки при резонансе напряжений равно потерям, вносимым сопротивлением RШ в индуктивность L1 на частоте резонанса напряжений. 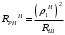 , (2.2) , (2.2)где 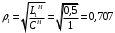 . .Определим нормированное сопротивление нагрузки при резонансе напряжений по (2.2). 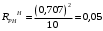 . .Проведенный анализ схемы позволяет предположить, что АЧХ входной функции нагрузки будет иметь характер, представленный на рисунке 2.5. 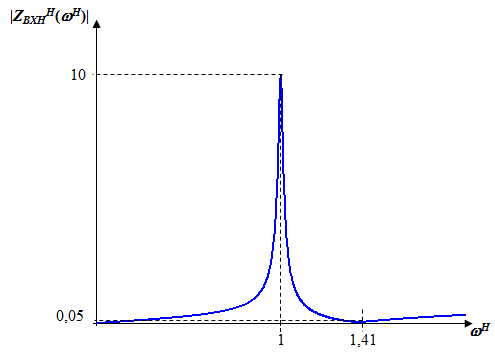 Рисунок 2.5 – Предполагаемый характер АЧХ входной функции нагрузки Для оценки характера ФЧХ, при параллельном соединении можно пренебречь большими сопротивлениями, при последовательном – меньшими [1]. Из рисунка 2.4 вытекает, что при 0 ZВХН900, при ZВХН00. При резонансе токов ФЧХ меняет знак с плюса на минус, при резонансе напряжений – с минуса на плюс. Предполагаемый характер ФЧХ входной функции цепи нагрузки представлен на рисунке 2.6. 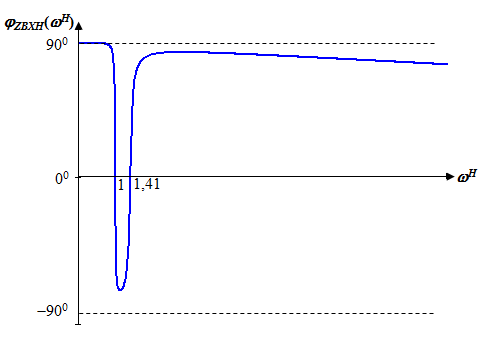 Рисунок 2.6 – Предполагаемый характер ФЧХ входной функции цепи нагрузки Цепь нагрузки представляет собой реактивный двухполюсник. У двухполюсника имеется только одна пара зажимов для внешнего воздействия и отклика. Тогда, если необходимо определить коэффициент передачи по напряжению, напряжения воздействия и отклика будут равны по амплитуде и фазе. Из этого следует, что АЧХ передаточной двухполюсника не зависит от частоты и равна единице, а ФЧХ двухполюсника не зависит от частоты и равна нулю. |
