курсовой проект СХЕМНЫЕ ФУНКЦИИ И ЧАСТОТНЫЕ ХАРАКТЕРИСТИКИ ЛИНЕЙНЫХ ЭЛЕКТРИЧЕСКИХ ЦЕПЕЙ. курсовой проект СХЕМНЫЕ ФУНКЦИИ И ЧАСТОТНЫЕ ХАРАКТЕРИСТИКИ ЛИНЕЙ. Курсовая работа по дисциплине Теория электрических цепей
 Скачать 0.71 Mb. Скачать 0.71 Mb.
|
Определение нулей и полюсов передаточной функции полной моделиОпредели нули и полюса передаточной функции полной модели (4.2) Нули передаточной функции: р01=0; р02,3=-0,05j1,413. Полюса передаточной функции: рп1=‒40; рп2=‒8,75; рп3,4=‒0,012j. Масштабный коэффициент К0=875. Аргумент масштабного коэффициента К0=00. Карта нулей и полюсов передаточной функции полной модели приведена на рисунке 4.9. 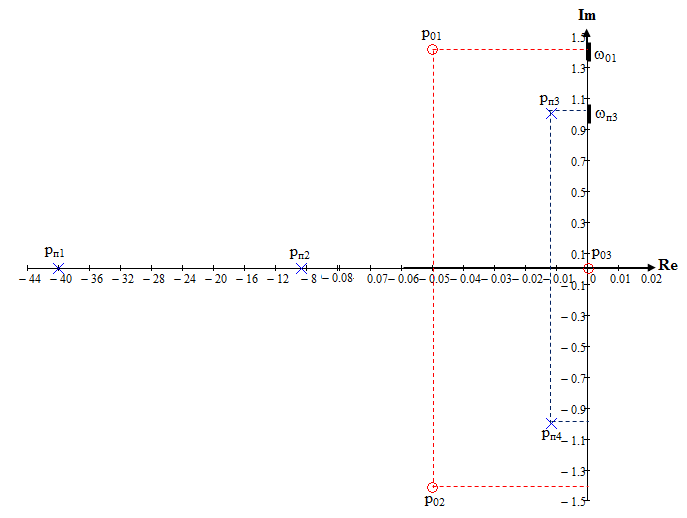 Рисунок 4.9 – Карта нулей и полюсов передаточной функции полной модели Предполагаемый характер ЧХ передаточной функции полной модели на основе карты нулей и полюсовОпределим предполагаемый характер частотных характеристик передаточной функции полной модели на основе анализа карты нулей и полюсов. Определим характер АЧХ. Так как есть ноль в начале координат, ZВХHН(0)=0. Так как полюсов больше, чем нулей, то 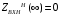 . .Минимальное значение АЧХ достигается в области нормированной частоты 01. Максимальное значение АЧХ достигается в области нормированной частоты п3. Предполагаемый характер АЧХ передаточной функции полнной модели на основе анализа карты нулей и полюсов приведен на рисунке 4.10. 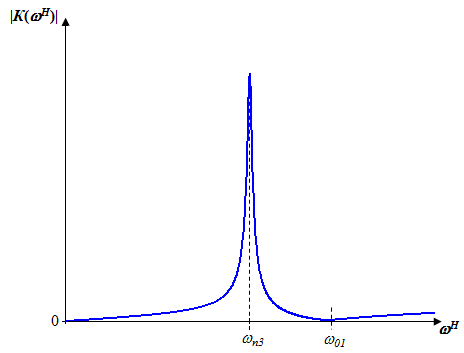 Рисунок 4.10 – Предполагаемый характер АЧХ передаточной функции полной модели на основе анализа карты нулей и полюсов Определим характер ФЧХ. Так как есть ноль в начале координат, Z(0)=900. Так как имеется равное количество полюсов на 1 больше, чем нулей, то Z()=900. Так как в районе частот п3, и 01 полюс и ноль расположены близко к мнимой оси, на этих частотах ожидается плавная смена ФЧХ на 900. Расчет ЧХ передаточной функции полной модели при Н=0,5 на основе карты нулей и полюсовПолюсно-нулевое изображение (ПНИ) передаточной функции полной модели для расчета ЧХ при Н=0,5 приведено на рисунке 4.11. 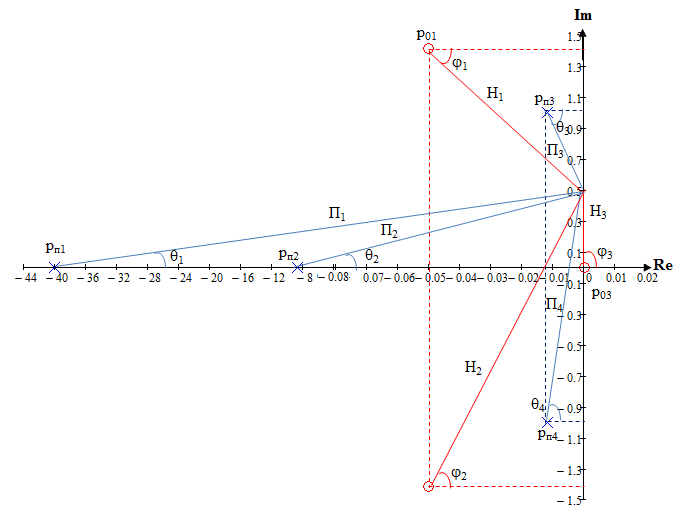 Рисунок 4.11 – ПНИ передаточной функции полной модели Определим частотные характеристики передаточной функции полной модели при Н=0,5. Рассчитанные по (2.8) модули (Нi) векторов, проведенных из нулей, и рассчитанные по (2.9) модули (Пi) векторов, проведенных из полюсов, приведены в таблице 4.3. Рассчитанные по (2.10) углы (i) векторов, проведенных из нулей, и рассчитанные по (2.11) углы (i) векторов, проведенных из полюсов, приведены в таблице 4.4. Таблица 2.1
Таблица 2.2
Вычислим значения ЧХ при Н=0,5. 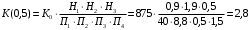 , ,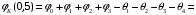 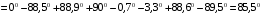 . .Получение выражений АЧХ и ФЧХ входной функции полной модели и расчет ЧХ при Н=0,51) Произведем замену во входной функции (4.1) p=j. 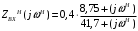 . (4.3) . (4.3)Модуль входной функции: 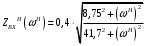 . (4.4) . (4.4)Аргумент входной функции: 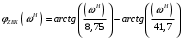 (4.5) (4.5)Графики АЧХ и ФЧХ входной функции полной модели приведены на рисунке 4.12 и рисунке 4.13 соответственно. 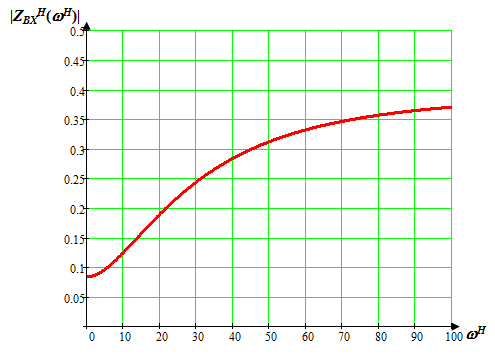 Рисунок 4.12 – График АЧХ входной функции полной модели 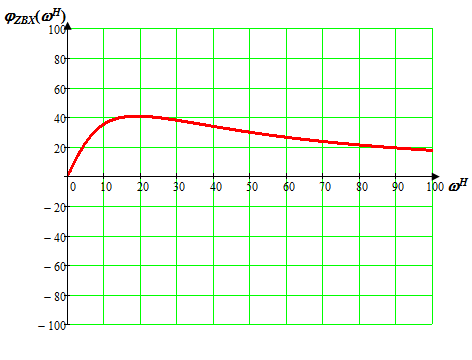 Рисунок 4.13 – График ФЧХ входной функции полной модели 2) Расчет ЧХ при Н=0,5. 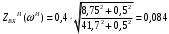 . .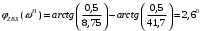 . .Результаты расчета совпадают с результатами, полученными при анализе карты нулей и полюсов. Получение выражений АЧХ и ФЧХ передаточной функции полной модели и расчет ЧХ при Н=0,51) Произведем замену в передаточной функции (4.2) p=j. 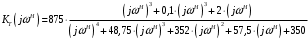 . .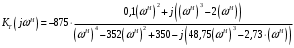 . (4.6) . (4.6)Модуль передаточной функции: 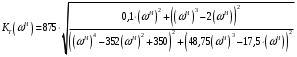 . (4.7) . (4.7)Аргумент передаточной функции: 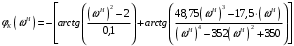 . (4.8) . (4.8)Графики АЧХ и ФЧХ передаточной функции полной модели приведены на рисунке 4.14 и рисунке 4.15 соответственно. 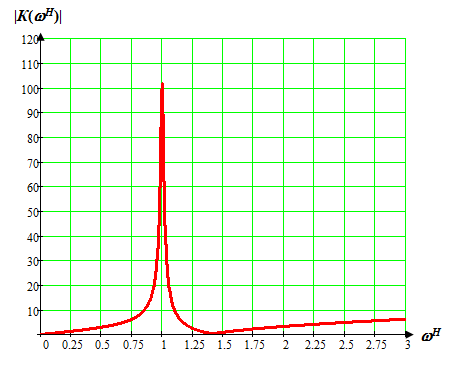 Рисунок 4.14 – График АЧХ передаточной функции полной модели 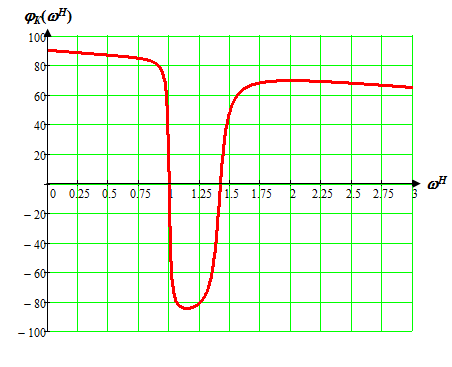 Рисунок 4.15 – График ФЧХ передаточной функции полной модели 2) Расчет ЧХ при Н=0,5. 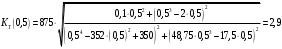 , ,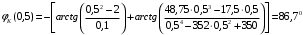 . .Результаты расчета совпадают с результатами, полученными при анализе карты нулей и полюсов. Оценка устойчивости и фазоминимальности цепи по карте нулей и полюсов1) Цепь устойчива, если нули и полюса входной функции и полюса передаточной функции находятся в левой полуплоскости, то есть являются полиномами Гурвица. У входной и передаточной функций исследуемой цепи нет нулей и полюсов в правой полуплоскости, следовательно, цепь устойчива по критерию Гурвица. 2) Так как у передаточной функции нет нулей в правой полуплоскости, цепь является фазоминимальной. Автоматизированный расчет АЧХ и ФЧХ входной и передаточной функцийМоделирование проводилось в программе Orcad. Схема модели для исследования частотных характеристик цепи приведена на рисунке 4.16. 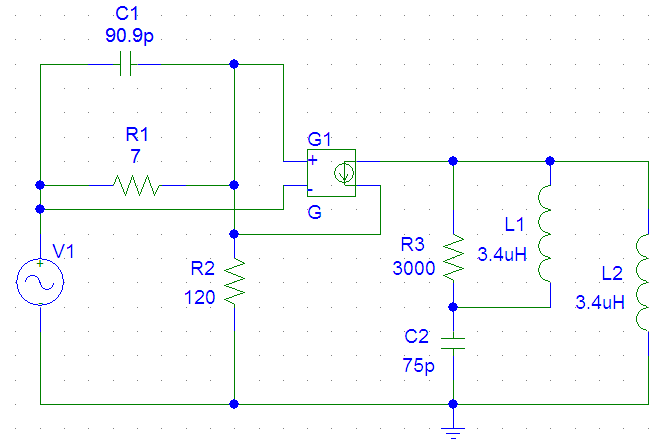 Рисунок 4.16 – Схема модели цепи для исследования частотных характеристик цепи Результаты моделирования АЧХ и ФЧХ входной функции в программе ORCAD приведены на рисунках 4.17 и 4.18 соответственно. Результаты моделирования соответствуют рассчитанным при анализе ПНИ и при анализе комплексной функции. ZBXH(0,5)=0,079, ZBX(0,5)=3,20. Результаты моделирования АЧХ и ФЧХ передаточной функции в программе ORCAD приведены на рисунках 4.19 и 4.20 соответственно. Результаты моделирования соответствуют рассчитанным при анализе ПНИ и при анализе комплексной функции. К(0,5)=3,1, К(0,5)=85,90. 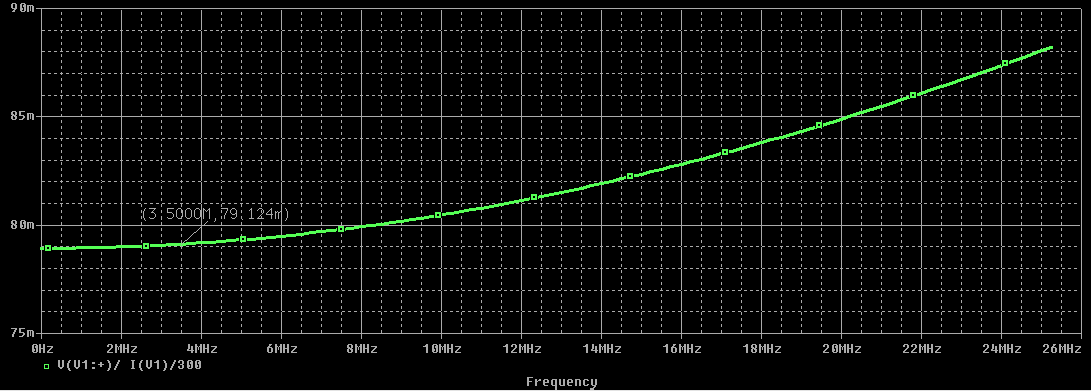 Рисунок 4.17 – Результаты моделирования АЧХ входной функции цепи 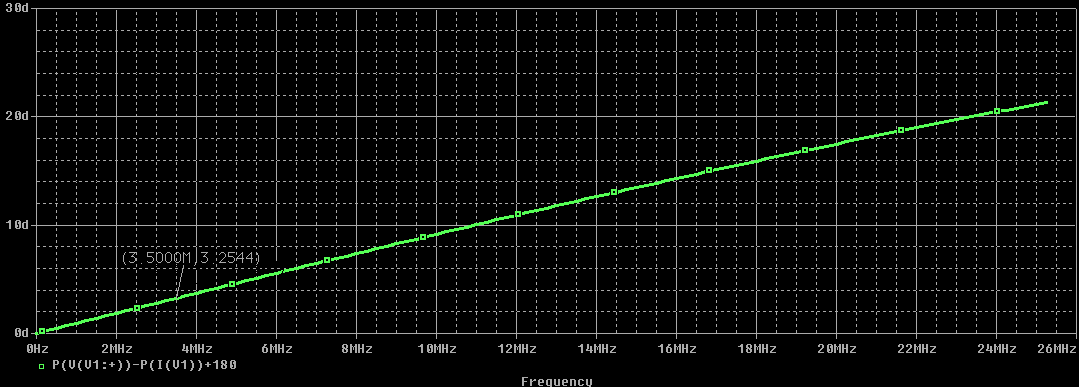 Рисунок 4.18 – Результаты моделирования ФЧХ входной функции цепи 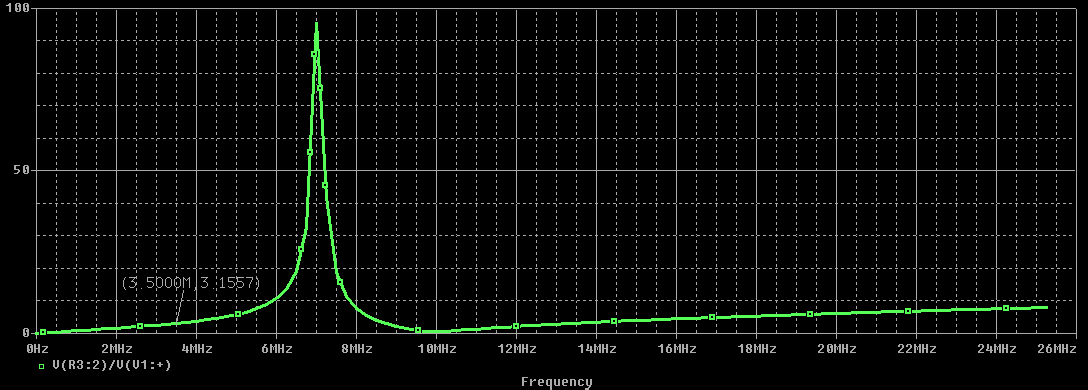 Рисунок 4.19 – Результаты моделирования АЧХ передаточной функции цепи 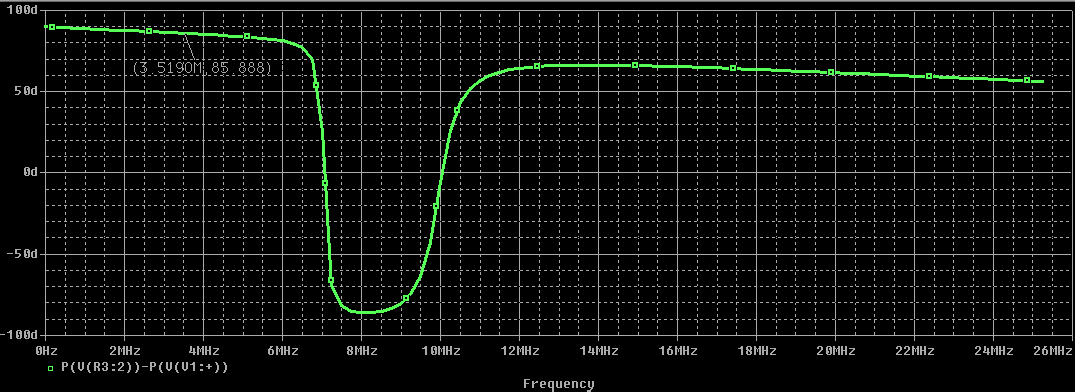 Рисунок 4.20 – Результаты моделирования ФЧХ передаточной функции цепи Представление входного сопротивления полной цепи последовательной и параллельными моделями1) Расчетные значения для входного сопротивления цепи на частоте 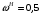 : :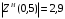 ; ;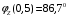 . .Комплексное входное сопротивление цепи: 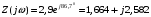 . .Элементы последовательной модели: 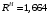 ; ;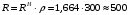 Ом. Ом.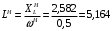 ; ;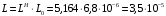 Гн=35 мкГн. Гн=35 мкГн.Параметры последовательной модели: R==500 Ом; L==35 мкГн. Схема последовательной модели цепи приведена на рисунке 4.21.  Рисунок 4.21 – Последовательная модель цепи 2) Комплексная входная проводимость цепи: 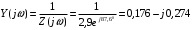 Элементы параллельной модели: 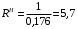 . .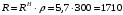 Ом. Ом.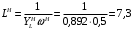 ; ;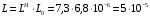 Гн=50 мкГн. Гн=50 мкГн.Параметры параллельной модели: R||=1710 Ом; L||=50 мкГн. Схема параллельной модели цепи приведена на рисунке 4.22. 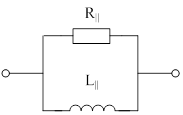 Рисунок 4.22 – Параллельная модель цепи ВыводыПри выполнении работы был проведен анализ модели избирательной нагрузки и модели транзистора с избирательной нагрузкой с использованием следующих методов: метод непосредственного анализа схемы электрической цепи; исследование схемных функций; автоматизированный расчет с использованием специальной программы. Количественное сравнение результатов расчета ЧХ полной модели различными методами приведено в таблице. Таблица – Количественное сравнение результатов расчета ЧХ полной модели различными методами
При анализе цепи всеми методами были получены практически одинаковые численные результаты требуемых частотных характеристик, что подтверждает правильность выполненных расчетов. Каждый из методов анализа имеет свои достоинства и недостатки. Преимуществом метода непосредственного анализа схемы является возможность оценки частотных характеристик на этапе синтеза схемы. Но при использовании этого метода получаются приближенные результаты и эти методом сложно оценить физическую реализуемость и устойчивость электрической цепи. При автоматизированном расчете можно получить точные частотные характеристики цепи, оценить ее устойчивость и физическую реализуемость, но данный метод не дает представления о физических процессах, протекающих в цепи, поэтому при появлении ошибок в проектируемой схеме их будет достаточно сложно устранять. Анализ схемных функций дает точные результаты при хорошей наглядности. Недостатком этого метода является большая трудоемкость при анализе сложных схем. Список использованных источников1 Мельникова И.В. Схемные функции. Методические указания по выполнению курсовой работы. – Томск: ФДО, ТУСУР, 2017. – 81с. 2 Попова А.И. Основы теории цепей : учебное пособие/ А.И. Попова, К.Ю. Попова, И.В. Мельникова; под общ. ред. А.И. Поповой. – Томск : ФДО, ТУСУР, 2017. – Ч. 2. – 179 с. 3 Образовательный стандарт вуза ОС ТУСУР 01-2013. Работы студенческие по направлениям подготовки и специальностям технического профиля. Общие требования и правила оформления (Утвержден и введен в действие Приказом ректора ТУСУР от 03.12.2013 г. №14103) [Электронный ресурс]: – Режим доступа: https://regulations.tusur.ru/documents/70. |
