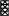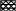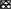tпр = 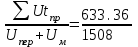 = 0,42 ч; = 0,42 ч;
в) tор = 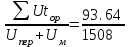 = 0,062 ч; = 0,062 ч;
г) tрасф = 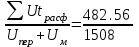 = 0,32ч. = 0,32ч.
,
Затрату вагоно-часов на накопление и средний простой вагона под накоплением можно определять по безномерному способу, как это показано в табл. 18.
Таблица 18
Часы суток
|
Число вагонов
|
Вагоно-часы
|
Поступило в сортировочный парк
|
Закончено накопление
|
Остаток
|
-
|
-
|
274
|
18 – 19
|
52
|
52
|
274
|
19 – 20
|
104
|
-
|
378
|
20 – 21
|
52
|
52
|
378
|
21 - 22
|
104
|
208
|
274
|
22 - 23
|
-
|
-
|
274
|
23 - 24
|
156-4+8
|
104
|
330
|
24 – 01
|
-
|
-
|
330
|
01 - 02
|
52
|
52
|
330
|
02 - 03
|
52
|
52
|
330
|
03 - 04
|
104-7+6
|
156
|
277
|
04 - 05
|
52
|
104
|
225
|
05 - 06
|
104
|
52
|
277
|
06 - 07
|
-
|
-
|
277
|
07 - 08
|
104
|
104
|
277
|
08 - 09
|
52-3
|
52
|
274
|
09 - 10
|
52
|
-
|
326
|
10 - 11
|
104
|
104
|
326
|
11 - 12
|
-
|
-
|
326
|
12 - 13
|
52
|
156
|
222
|
13 - 14
|
104-8+15
|
104
|
229
|
14 - 15
|
52
|
-
|
281
|
15 – 16
|
52
|
52
|
281
|
16 – 17
|
-
|
-
|
281
|
17 – 18
|
104-7
|
104
|
274
|
Итого
|
1508
|
1508
|
7051
|
г) tнак = 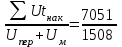 = 4.67 ч. = 4.67 ч.
Более точно простой под накоплением можно находить поструйно по каждому назначению. При этом затрата вагоно-часов на накопление одного состава определяется как площадь геометрической фигуры, показанной на рис. 13, ваг.-ч.:
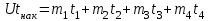 . (21) . (21)

Рис. 13. Процесс накопления состава.
Затрата вагоно-часов на ожидание формирования, формирование и перестановку, а также среднее время нахождения вагонов под этими операциями определяется в табл. 19.
Таблица 19
№ поездов своего формирования
|
Число вагонов в составе
|
Продолжительность, ч
|
Вагоно-часы
|
ожидания формирования
|
формирования и перестановки
|
ожидания формирования
|
формирования и перестановки
|
2001
|
52
|
-
|
0,3
|
-
|
15.6
|
2003
|
52
|
-
|
0,3
|
-
|
15.6
|
2007
|
52
|
-
|
0,3
|
-
|
15.6
|
2009
|
52
|
-
|
0,3
|
-
|
15.6
|
3202
|
52
|
0.48
|
0,3
|
24.96
|
15.6
|
2402
|
52
|
-
|
0,3
|
-
|
15.6
|
2013
|
52
|
-
|
0,3
|
-
|
15.6
|
2015
|
52
|
-
|
0,3
|
-
|
15.6
|
2017
|
52
|
-
|
0,3
|
-
|
15.6
|
3401
|
52
|
0.73
|
0,72
|
37.96
|
37.44
|
3422
|
52
|
2.37
|
0,72
|
123.24
|
37.44
|
2021
|
52
|
0.47
|
0,3
|
24.44
|
15.6
|
2025
|
52
|
-
|
0,3
|
-
|
15.6
|
2029
|
52
|
0.4
|
0,3
|
20.8
|
15.6
|
2035
|
52
|
-
|
0,3
|
-
|
15.6
|
3452
|
52
|
1.92
|
0,72
|
99.84
|
37.44
|
2037
|
52
|
-
|
0,3
|
-
|
15.6
|
2039
|
52
|
-
|
0,3
|
-
|
15.6
|
3001
|
52
|
0.48
|
0,3
|
24.96
|
15.6
|
2041
|
52
|
3.38
|
0,3
|
175.76
|
15.6
|
2043
|
52
|
-
|
0,3
|
-
|
15.6
|
2045
|
52
|
-
|
0,3
|
-
|
15.6
|
3102
|
52
|
3.42
|
0,3
|
177.84
|
15.6
|
2049
|
52
|
-
|
0,3
|
-
|
15.6
|
2051
|
52
|
-
|
0,3
|
-
|
15.6
|
2053
|
52
|
-
|
0,3
|
-
|
15.6
|
2057
|
52
|
-
|
0,3
|
-
|
15.6
|
2059
|
52
|
-
|
0,3
|
-
|
15.6
|
2061
|
52
|
-
|
0,3
|
-
|
15.6
|
Итого
|
1508
|
-
|
-
|
709.8
|
517.92
|
д) tоф = 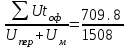 = 0,47 ч; = 0,47 ч;
е) tф = 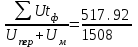 = 0,34 ч. = 0,34 ч.
Аналогично рассчитываются затраты вагоно-часов в ожидании отправления и на обработку в парке отправления, а также средний простой вагона под этими операциями. Расчет сводится в табл. 20.
№ поездов своего формирования
|
Число вагонов в составе
|
Продолжительность, ч
|
|
Вагоно-часы
|
|
|
|
обработки по отправлению
|
ожидания отправления
|
Ожидание
обработки
|
под обработкой
|
в ожидании отправления
|
Ожидание отправления
|
2001
|
52
|
0.67
|
1.87
|
-
|
34.84
|
97.24
|
-
|
2003
|
52
|
0.67
|
1.7
|
0.67
|
34.84
|
88.4
|
34.84
|
2007
|
52
|
0.67
|
-
|
0.02
|
34.84
|
-
|
1.04
|
2009
|
52
|
0.67
|
-
|
0.02
|
34.84
|
-
|
1.04
|
3202
|
52
|
0.67
|
-
|
0.92
|
34.84
|
-
|
47.84
|
2402
|
52
|
0.67
|
0.03
|
0.68
|
34.84
|
1.56
|
35.36
|
2013
|
52
|
0.67
|
-
|
0.5
|
34.84
|
-
|
26
|
2015
|
52
|
0.67
|
0.13
|
1
|
34.84
|
6.76
|
52
|
2017
|
52
|
0.67
|
0.47
|
1.18
|
34.84
|
24.44
|
61.36
|
3401
|
52
|
0.67
|
-
|
-
|
34.84
|
-
|
-
|
3422
|
52
|
0.67
|
1.8
|
-
|
34.84
|
93.6
|
-
|
2021
|
52
|
0.67
|
-
|
0.85
|
34.84
|
-
|
44.2
|
2025
|
52
|
0.67
|
0.35
|
0.65
|
34.84
|
18.2
|
33.8
|
2029
|
52
|
0.67
|
-
|
1.55
|
34.84
|
-
|
80.6
|
2035
|
52
|
0.67
|
0.06
|
1.05
|
34.84
|
3.12
|
54.6
|
3452
|
52
|
0.67
|
-
|
-
|
34.84
|
-
|
-
|
2037
|
52
|
0.67
|
-
|
1.15
|
34.84
|
-
|
59.8
|
2039
|
52
|
0.67
|
1.93
|
0.05
|
34.84
|
100.36
|
2.6
|
3001
|
52
|
0.67
|
-
|
-
|
34.84
|
-
|
-
|
2041
|
52
|
0.67
|
-
|
0.1
|
34.84
|
-
|
5.2
|
2043
|
52
|
0.67
|
-
|
0.48
|
34.84
|
-
|
24.96
|
2045
|
52
|
0.67
|
0.43
|
2.53
|
34.84
|
22.36
|
131.56
|
3102
|
52
|
0.67
|
-
|
0.35
|
34.84
|
-
|
18.2
|
2049
|
52
|
0.67
|
0.13
|
0.97
|
34.84
|
6.76
|
50.44
|
2051
|
52
|
0.67
|
-
|
0.97
|
34.84
|
-
|
50.44
|
2053
|
52
|
0.67
|
-
|
0.85
|
34.84
|
-
|
44.2
|
2057
|
52
|
0.67
|
-
|
0.03
|
34.84
|
-
|
1.56
|
2059
|
52
|
0.67
|
-
|
0.22
|
34.84
|
-
|
11.44
|
2061
|
52
|
0.67
|
0.5
|
0.88
|
34.84
|
26
|
45.76
|
Итого
|
1508
|
|
|
|
1010.36
|
488.8
|
918.84
|
ж) tот = 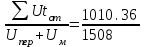 = 0,67 ч; = 0,67 ч;
з) tоо = 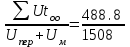 = 0,32 ч. = 0,32 ч.
t (ожидания обработки) =918.84/1508=0.6
Подставив найденные величины в формулу (20), получим средний простой транзитного вагона с переработкой:
tnep = 0,42 + 0,062 + 0,32 + 0.083 + 4.67 + 0,47 + 0,34 +0.67 + 0,32 + 0.6 = 7.95 ч.
На основании предыдущих расчетов строится график расчлененного простоя транзитного вагона с переработкой (рис. 14).
Элементы простоя
|
Норма, ч
|
Время, ч
|
1 2 3 4 5 6 7 8
|
1. Обработка в ПП tпр
|
 0,42 0,42
|

|
|
|
|
|
|
|
|
|
2. t опр ожидание обработки
|
0,083
|
|
|
|
|
|
|
|
|
|
3. Ожидание роспуска tор
|
0,062
|
|
|
|
|
|
|
|
|
|
4. Расформирование tрасф
|
0,32
|

|
|
|
|
|
|
|
|
|
5. Накопление tнак
|
4,67
|
|
|
|
|
|

|
|
|
|
6. Ожидание формирования tоф
|
0,47
|
|
|
|
|
|
|

|
|
|
7. Формирование и перестановка tф
|
0,34
|
|
|
|
|
|
|
 
|
|
|
8.t ожоб Ожидание обработки
|
0.6
|
|
|
|
|
|
|
 
|
|
|
9. Обработка в ПО tот
|
0,67
|
|
|
|
|
|
|
|
|
|
10. Ожидание отправления tоо
|
0,32
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Общая продолжительность tпер
|
7.95
|
|
|
|
|
|
|
|
|
|
Рис. 14. Расчлененный простой вагона
Расчет среднего простоя вагонов по элементам и в целом по станции можно определить с использованием компьютерных программ [5]. |
 Скачать 1.49 Mb.
Скачать 1.49 Mb.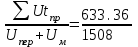 = 0,42 ч;
= 0,42 ч;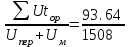 = 0,062 ч;
= 0,062 ч;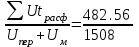 = 0,32ч.
= 0,32ч.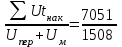 = 4.67 ч.
= 4.67 ч.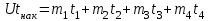 . (21)
. (21)
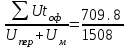 = 0,47 ч;
= 0,47 ч;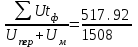 = 0,34 ч.
= 0,34 ч.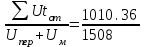 = 0,67 ч;
= 0,67 ч;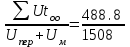 = 0,32 ч.
= 0,32 ч.