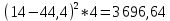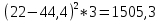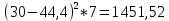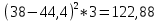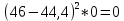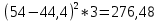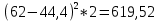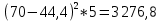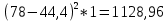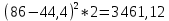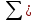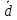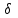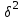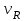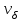Вариант 2 Куликов Лев Статистика. Курсовая работа по курсу Статистика (теория статистики, социальноэкономическая статистика)
 Скачать 181.25 Kb. Скачать 181.25 Kb.
|
|
М  ИНИСТЕРСТВО НАУКИ И ВЫСШЕГО ОБРАЗОВАНИЯ РОССИЙСКОЙ ФЕДЕРАЦИИ ИНИСТЕРСТВО НАУКИ И ВЫСШЕГО ОБРАЗОВАНИЯ РОССИЙСКОЙ ФЕДЕРАЦИИфедеральное государственное бюджетное образовательное учреждение высшего образования «МОСКОВСКИЙ АВТОМОБИЛЬНО-ДОРОЖНЫЙ ГОСУДАРСТВЕННЫЙ ТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ (МАДИ)» Заочный факультет Кафедра «МЕНЕДЖМЕНТ» Курсовая работа по курсу «Статистика (теория статистики, социально-экономическая статистика)» Вариант № 2 В  ыполнила: студент гр.2ЗбМОс2 Куликов Лев Сергеевич ыполнила: студент гр.2ЗбМОс2 Куликов Лев Сергеевич (подпись) Проверил: доцент, к.т.н. Яшуков Александр Владимирович Москва 2021 Содержание Введение 3 1 Часть. Ряды распределения 4 2 Часть. Ряды динамики 13 3 Часть. Измерение сезонных колебаний 19 4 часть. Статистика населения 22 ВведениеКурсовая работа является одним из основных этапов самостоятельной работы студентов. Цель выполнения курсовой работы - закрепление и углубление знаний по статистике, методическое обеспечение статистического исследования экономической проблемы. Изучение и переработка теоретического материала, сбор и обработка статистической информации прямо связаны с изучением дисциплин, предусмотренных учебным планом специальности. Основной задачей курсовой работы является статистическое исследование социально-экономических процессов на основе системы статистических показателей. В процессе выполнения курсовой работы студент должен показать: Знание основных экономических законов и категорий; Умение выбрать ключевые вопросы в развитии объекта и методологии исследования; Способность формирования системы экономических показателей, характеризующих развитие объекта исследования; Владение методикой статистического анализа объекта исследования с использованием основных математико-статистических методов; Умение интерпретировать результаты исследований. 1 Часть. Ряды распределенияСодержание раздела: В данном разделе необходимо изучить составление группировки. Расчет различных видов средних величин и показателей вариации, анализ дисперсии. Важнейшей частью статистического анализа является построение рядов распределения (структурной группировки) с целью выделения характерных свойств и закономерностей изучаемой совокупности. В зависимости от того, какой признак (количественный или качественный) взят за основу группировки данных, различают соответственно типы рядов распределения. Статистический ряд распределения — это упорядоченное распределение единиц совокупности на группы по определенному варьирующему признаку. В зависимости от признака статистические ряды распределения делятся на следующие: атрибутивные (качественные); вариационные (количественные); а) дискретные; б) интервальные. Атрибутивными называют ряды распределения, построенные по качественным признакам. Ряд распределения принято оформлять в виде таблиц. Атрибутивные ряды распределения характеризуют состав совокупности по тем или иным существенным признакам. Взятые за несколько периодов, эти данные позволят исследовать изменение структуры. Вариационным называют ряды распределения, построенные по количественному признаку. Любой вариационный ряд состоит из элементов: вариантов и частот. Вариантами считаются отдельные значения признака, которые он принимает в вариационном ряду, т.е. конкретное значение варьирующего признака. Частоты — это численности отдельных вариантов или каждой группы вариационного ряда, т.е. это числа, показывающие, как часто встречаются те или иные варианты в ряду распределения. Сумма всех частот определяет численность всей совокупности, ее объем. Выделяют три формы вариационного ряда: ранжированный ряд, дискретный ряд и интервальный ряд. Начнем конкретные операции со статистической совокупностью S. Имеются данные о заработной плате работников компании. Первоначальный статистический ряд получаем как ряд данных, записанных в порядке их поступления в статистическую совокупность S: Таблица 1.1 Первоначальный ряд
Число наблюдений (объем ряда) N= 30 Первоначальный ряд, построенный в порядке возрастания или убывания значений признака, называют ранжированным рядом. Ранжирование позволяет легко разделить количественные данные по группам, сразу обнаружить наименьшее и наибольшее значения признака, выделить значения, которые чаще всего повторяются. В реальной статистической практике чаще используется построение ряда в порядке возрастания. А) Строим первоначальный ряд, построенный в порядке возрастания или убывания значений признака, называют ранжированным рядом. Таблица 1.2 Ранжированный ряд
N=30 ед. Для того чтобы построить дискретный и интервальные вариационные ряды определим повторение значения признака в Xi в ранжированном ряду: Дискретный ряд — это такой вариационный ряд, в основу построения которого положены признаки с прерывным изменением (дискретные признаки). Дискретный вариационный ряд представляет таблицу, которая состоит из двух граф. В первой графе указывается конкретное значение признака, а во второй - число единиц совокупности с определенным значением признака. Б) Определим повторение значения признака Xi ранжированном ряду: Таблица 1.3 Дискретный ряд
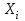 – количественное обозначение признака. – количественное обозначение признака.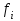 – частота (или повторяемость), т.е. число, показывающее какое количество раз встречаются те или иные значения признака в ряду распределения. – частота (или повторяемость), т.е. число, показывающее какое количество раз встречаются те или иные значения признака в ряду распределения.Проверка общая сумма F=N=30 Таблица 1.4 Интервальный ряд
По условию задания необходимо построить 10 групп с равными интервалами. Величина интервала может быть определена как: 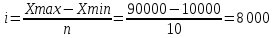 Вычислим для полученного интервального ряда следующие величины: Среднюю Средняя взвешенная для дискретного ряда: 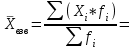 где 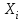 – варианта (значение) признака; – варианта (значение) признака; 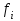 – частота, показывающая, сколько раз встречается i-e значение признака. – частота, показывающая, сколько раз встречается i-e значение признака.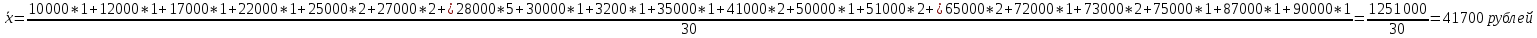 Средняя взвешенная для интервального ряда: 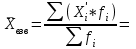 где 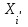 - середина соответствующего интервала значения признака. - середина соответствующего интервала значения признака.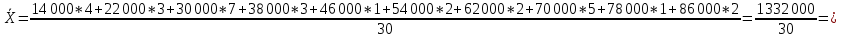 44 400рублей 44 400рублейВычислим моду Мода – это вариант, наиболее часто встречающийся в данном вариационном ряду. В дискретном ряду мода определяется без вычисления как значение признака с наибольшей частотой. 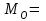 28 000 (Значение ряда 28000 встречается всех больше (5 раз)) 28 000 (Значение ряда 28000 встречается всех больше (5 раз))В интервальном вариационном ряду, тем более при непрерывной вариации признака, строго говоря, каждое значение признака встречается только один раз. Модальным интервалом является интервал с наибольшей частотой. 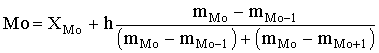 где ХMo – нижнее значение модального интервала; mMo – число наблюдений или объем взвешивающего признака в модальном интервале (в абсолютном либо относительном выражении); mMo-1 – то же для интервала, предшествующего модальному; mMo+1 – то же для интервала, следующего за модальным; h – величина интервала изменения признака в группах. 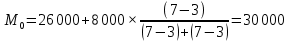 Вывод: наиболее частым показателем в дискретном ряду, т.е. модой, является 28 000 руб., в интервальном – 30 000 руб. Вычислим медиану Медиана – это значение варьирующего признака, который приходится на середину упорядоченного ряда. Медиана рассчитывается по-разному в дискретных и интервальных рядах. Для дискретного ряда: n=30 n=2m, m =15 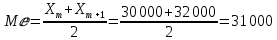 В интервальном ряду распределения сначала указывают интервал, в котором находится медиана. Медианным является первый интервал, в котором сумма накопленных частот превысит половину общего числа наблюдении. 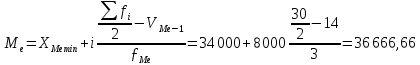 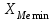 – нижняя граница медианного интервала; – нижняя граница медианного интервала;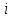 -интервал; -интервал;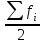 - половина от суммы накопленных частот; - половина от суммы накопленных частот;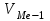 - накопленная частота, предшествующая медиане; - накопленная частота, предшествующая медиане;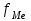 - частота медианного интервала. - частота медианного интервала.Вывод: в дискретном ряду показателем, приходящимся на середину ряда, т.е. медианой, является 31 000 руб., в интервальном – 36 666,66 руб. Вычислим размах вариации Размах вариаций является ее простейшим показателем. Он определяется как разность между максимальное и минимальное значение признака. Недостаток того показателя заключается в том, что он зависит только от двух крайних значений признака (min, max) и не характеризует колеблимость внутри совокупности. 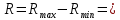 90 000 – 10 000 = 80 000 90 000 – 10 000 = 80 000 Вычислим среднее линейное отклонение; Среднее линейное отклонение является средней величиной абсолютных значений отклонений от средней арифметической. Отклонения берутся по модулю, т.к. в противном случае, из-за математических свойств средней величины, они всегда были бы равны нулю. Таблица 1.5 Вспомогательная таблица
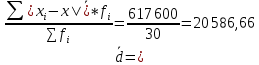 рублей рублейСреднее квадратическое отклонение; Среднее квадратическое отклонение определяется как корень из дисперсии. Среднее квадратическое отклонение по своей величине всегда превышает значение среднего линейного отклонения в соответствии со свойством мажорантности средних. 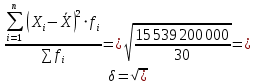 22 759,02 22 759,02 Дисперсия Дисперсия (средний квадрат отклонений) имеет наибольшее применение в статистике как показатель меры колеблимости. Дисперсия является именованным показателем. Она измеряется в единицах соответствующих квадрату единиц измерения изучаемого признака. Дисперсия – является мерой рассеивания значений варьирующего. 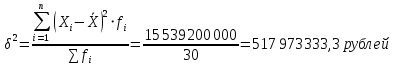 Вывод: разница между максимальным и минимальным значением признака составила 80 000 рублей, среднее линейное отклонение – 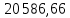 рубля, среднее квадратическое отклонение – 22 759,02 рубля, дисперсия – 517 973 333,3 рублей. рубля, среднее квадратическое отклонение – 22 759,02 рубля, дисперсия – 517 973 333,3 рублей. Коэффициент вариации; При сравнении колеблемости различных признаков в одной и той же совокупности или же при сравнении колеблемости одного и того же признака в нескольких совокупностях с различной величиной средней арифметической используются относительные показатели вариации. Они вычисляются как отношение абсолютных показателей вариации к средней арифметической (или медиане) и чаще всего выражаются в процентах. Коэффициент вариации используют для сравнения рассеивания двух и более признаков, имеющих различные единицы измерения. Коэффициент вариации представляет собой относительную меру рассеивания, выраженную в процентах. Он вычисляется по формуле: 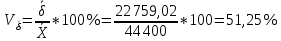 Вывод: коэффициент вариации равен 51,25 %, что больше 33 %, значит совокупность неоднородна. Коэффициент осцилляции; 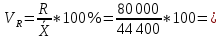 180,2 % 180,2 %Вывод: процентное отношение размаха вариации к средней больше на 180,2%. Линейный коэффициент вариации 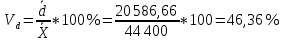 Вывод: отношение среднего линейного отклонения к средней составило 46,36 %. Таблица 1.6 Итоговая таблица по показателям
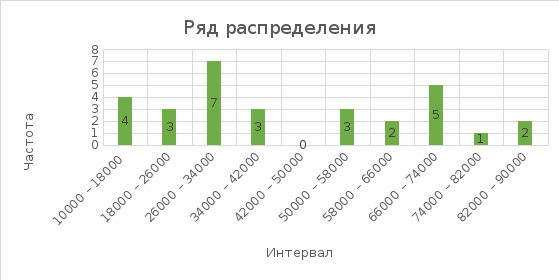 Д) Графическое изображения ряда распределения в виде гистограммы, полигона и огивы. Д) Графическое изображения ряда распределения в виде гистограммы, полигона и огивы.Рис. 1.1 Графическое изображения ряда распределения в виде гистограммы 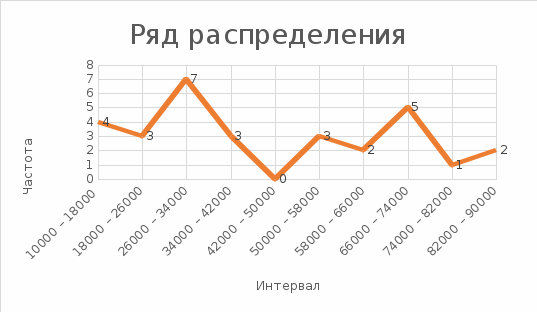 Рис. 1.2 Графическое изображения ряда распределения в виде полигона 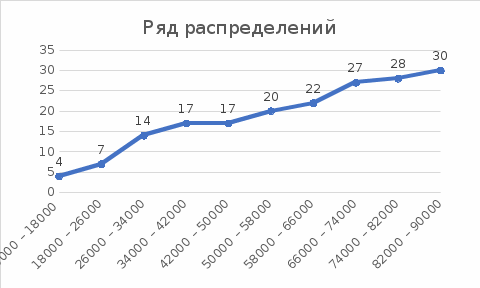 Рис. 1.3 Графическое изображения ряда распределения в виде огивы | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||

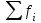 (сумма частот кумулятивных)
(сумма частот кумулятивных)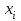
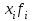
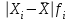
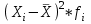 (млн. руб.)
(млн. руб.)