уравнения с модулем. курсовая уровнения с модулем. Курсовая работа содержание

Название	Курсовая работа содержание
Анкор	уравнения с модулем
Дата	25.05.2022
Размер	163.47 Kb.
Формат файла
Имя файла	курсовая уровнения с модулем.docx
Тип	Курсовая #548749

КУРСОВАЯ РАБОТА

Содержание

Введение……………………………………………………………………..……3

Глава 1. Методика изучения рациональных уравнений с модулем ……..……5

1.1. Методика изучения рациональных и дробно-рациональных уравнений………………………………………………………………………….5

1.2. Рациональные и дробно-рациональные уравнения с параметром ……8

Глава 2. Методики решения рациональных уравнений с модулями…………12

2.1. Основные способы, используемые при решении уравнений, содержащих модуль….…………………………………………………………………………12

2.2. Методы повышения эффективности изучения рациональных уравнений с модулем…………………………………………………………………………..15

Заключение………………………………………………………………………22

Список литературы……………………………………………….…………….25

Введение

Уравнения в школьном курсе алгебры занимают ведущее место. На их изучение отводится времени больше, чем на любую другую тему. Действительно, уравнения не только имеют важное теоретическое значение, но и служат чисто практическим целям.

Подавляющее большинство задач о пространственных формах и количественных отношениях реального мира сводится к решению различных видов уравнений. Овладевая способами их решения, мы находим ответы на различные вопросы из науки и техники (транспорт, сельское хозяйство, промышленность, связь и т. д.).

Так же для формирования умения решать уравнения большое значение имеет самостоятельная работа учащегося при обучении решения уравнений. Проблема методики формирования умений работы является актуальной для учителей всех школьных предметов, в том числе и для учителей математики. Ее решение важно еще и с той точки зрения, что для успешного овладения современным содержанием школьного математического образования необходимо повысить эффективность процесса обучения в направлении активизации деятельности учащихся. Для этого требуется четко определить систему умений и навыков, овладение которыми приводит к выполнению работ различного характера.

Важным также является раскрытие процесса формирования умений и навыков работы при обучении курсам математики, при этом необходимо показать, как в ходе преподавания математики учитель может осуществить формирование у учащихся отмеченных выше умений и навыков.

Цель: исследовать методы решения рациональных уравнений с модулем и методики их изучения.

Задачи:

1. Изучить рациональные и дробно- рациональные уравнения;

2. Рассмотреть методику изучения уравнений в 9 классе;

3. Рассмотреть рациональные и дробно-рациональные уравнения с параметром;

4. изучение методики решения уравнений с параметром.

Объект исследования: изучение уравнений рациональных уравнений с модулем.

Предмет исследования: решение уравнений с модулем.

Теоретической основой исследования послужили работы таких авторов как Фролов А.В., Трифонов Е.А.

В работе использованы методы системного анализа, синтеза, дидактического изучения материала.

Курсовая работа состоит из введения, двух глав, заключения и списка литературы.

Глава 1. Методика изучения рациональных уравнений с модулем

Методика изучения рациональных и дробно-рациональных уравнений

В различных учебниках применяется разная терминология, относящаяся, по существу, к одному и тому же классу уравнений. В этом отношении необходимо быть чрезвычайно внимательным и употреблять только те термины, которые введены в учебнике, причем именно в том смысле, который им придается.

В этой теме необходимо научить учеников решать дробно-рациональные уравнения сведением их к линейным или квадратным уравнениям.

Начинаем с рассмотрения некоторых уравнений, к примеру:

а) 3х+4=2(1-х²) б) (х+1)\2=(х²-х-1)\3 в) х²-(5+1)\3

г) х+1=

После обсуждения вводится теория:

Уравнения, в которых обе части являются рациональным выражением, называют рациональным уравнением. В примере рациональными уравнениями являются а-г. Рациональные уравнения, в которых обе части являются целыми выражениями, называют целыми уравнениями.

В примере целыми будут уравнения а, б (квадратные уравнения). Рациональное уравнение, в котором хотя бы одна из частей является дробным выражением, называют дробно- рациональным уравнением. В примере такими выражениями являются в-г.

Решение уравнений с модулем может быть самостоятельной задачей, но часто такие уравнения могут возникнуть при решении уравнений другого типа. Например, квадратных уравнений. Или иррациональных. Вот пример подобной ситуации: x2=16. Видно, что в правой части – квадрат числа 4:
x2=44. Казалось бы, теперь достаточно просто убрать квадраты слева и справа и получим линейное уравнение.

В таких ситуациях нужно быть предельно осторожным: ведь ты же помнишь простое правило: x2−−√=|x|? Вот и появляется на модуль:
x2=42 ⇔ x2−−√=42−−√ ⇔ |x|=4

Чтобы не теряться в таких случаях, давай разберемся, что из себя представляет решение уравнений с модулем.

Решение уравнений с модулем вида |x| = a

Уравнения такого вида решаем, основываясь на свойствах модуля, которые мы разобрали в теме «Модуль числа».

Давай разбираться на примерах. Необходимо решить уравнение вида
|x|=7 . Что такое |x|

Это просто x, если x больше либо равно нулю, или −x, если x меньше нуля.

То есть можно формализовано записать так:
|x|=7⇔[x=7, при x≥0−x=7, при x<0⇔[x=7x=−7

А если вот такое уравнение. |x|=−7 Рассуждения аналогичные:
|x|=−7⇔[x=−7, при x≥0−x=−7, при x<0⇔{x=−7x≥0⇒ решения нет{x=7x<0 ⇒ решения нет. Эти рассуждения можно было и обойти, вспомнив основное свойство модуля.

Основной способ решения рациональных уравнений состоит в преобразовании их в простейшие целые уравнения: линейные или квадратные.

При решении дробно- рациональных уравнений целесообразно:

1. Разложить все знаменатели дробей, входящих в уравнение, на множители.

2. Найти общий знаменатель этих дробей.

3. Умножить все члены данного уравнения на общий знаменатель.

4. Решить получившееся целое уравнение.

5. Из корней этого уравнения исключить те, которые обращают в нуль общий знаменатель данного уравнения.

В ходе решения дробно-рациональных уравнений необходимо установить, являются ли найденные корни целого уравнения допустимыми значениями переменной. Учащиеся нередко ошибаются, пропуская этот момент, поэтому надо настойчиво добиваться, чтобы в каждом случае алгоритм был выполнен до конца.

Пример 1:21/х+1• х(х+1)(х-2)≠0, х≠0, х≠2 и х≠-1

21х(х-2) + 6(х+1)(х-2) = 16х(х+1)

21х² – 42х + 6х² -6х-12=16х²+16х

11х² -64х -12=0

х₁= 6; х₂= -2\11 Ответ : -2/11; 6.

Пример 2: 2/(х-2)(х+2)-1/х(х-2)=(4-х)/х(х+2)

2/(х-2)(х+2)-1\х(х-2)=4-х/х(х+2) х(х-2)(х+2)≠0 х≠2, х≠-2 х≠0

2х – (х+2) = (4-х)(х-2)

2х – х – 2 = 4х – х² – 8 +2х

х² – 5х + 6 =0

х₁= 2; (не является корнем)

х₂= 3

Ответ: 3.

Модуль — одна из тех вещей, о которых вроде-бы все слышали, но в действительности никто нормально не понимает. Поэтому сегодня необходимо рассмотреть, посвящённый решению уравнений с модулями.

Считается, что модули — вообще тема относительно несложная. У многих учеников данная тема вызывает затруднения из-за общего пробела знаний по уравнениям.

Ещё один важный факт: модуль никогда не бывает отрицательным. Какое бы число мы ни взяли — хоть положительное, хоть отрицательное — его модуль всегда оказывается положительным (или в крайнем случае нулём). Именно поэтому модуль часто называют абсолютной величиной числа.

Кроме того, если объединить определение модуля для положительного и отрицательного числа, то получим глобальное определение модуля для всех чисел. А именно: модуль числа равен самому этому числу, если число положительное (или ноль), либо равен противоположному числу, если число отрицательное. Можно записать это в виде формулы.

Как быть в таком случае? Во-первых, надо раз и навсегда понять, что если правая часть уравнения окажется отрицательной, то уравнение не будет иметь корней — мы уже знаем, что модуль не может быть равен отрицательному числу.

А во-вторых, если права часть всё-таки положительна (или равна нулю), то можно действовать точно так же, как раньше: просто раскрыть модуль отдельно со знаком «плюс» и отдельно — со знаком «минус».

Данное замечание, возможно, покажется излишне сложным и неприменимым на практике. Однако в реальности вам могут встретиться куда более сложные задачи, нежели те, что мы сегодня разбираем. В них модули могут комбинироваться с многочленами, арифметическими корнями, логарифмами и т.д. И в таких ситуациях возможность понизить общую степень уравнения путём вынесения чего-либо за скобку.

Теперь хотелось бы разобрать ещё одно уравнение, которое на первый взгляд может показаться сложным. На нём теряются многие ученики — даже те, которые считают, что хорошо разобрались в модулях.

Тем не менее, это уравнение решается даже проще, чем то, что мы рассматривали ранее. И если вы поймёте почему, то получите ещё один приём для быстрого решения уравнений с модулями.

Что ж, привыкайте: в том и состоит сложность модуля, что ответы в таких уравнениях могут оказаться совершенно непредсказуемыми.

Куда важнее другое: мы только что разобрали универсальный алгоритм решения уравнения с модулем. И состоит этот алгоритм из следующих шагов:

Приравнять каждый модуль, имеющийся в уравнении, к нулю. Получим несколько уравнений;
Решить все эти уравнения и отметить корни на числовой прямой. В результате прямая разобьётся на несколько интервалов, на каждом из которых все модули однозначно раскрываются;
Решить исходное уравнение для каждого интервала и объединить полученные ответы.

Рациональные и дробно-рациональные уравнения, содержащие параметр

Функция вида P(x) = a₀ xⁿ + a ₁x^n-1 + a ₂x^n-2 + … + a _n-1x + a_n,

где n — натуральное, a₀, a₁,…, a_n — некоторые действительные числа, называется целой рациональной функцией [10].

Уравнение вида P(x) = 0, где P(x) — целая рациональная функция, называется целым рациональным уравнением [10].

Уравнение вида P₁(x) / Q₁(x) + P₂(x) / Q₂(x) + … + P_m(x) / Q_m(x) = 0, где P₁(x), P₂(x), … ,P_m(x), Q₁(x), Q₂(x), …, Q_m(x) — целые рациональные функции, называется рациональным уравнением.

Решение рационального уравнения P (x) / Q (x) = 0, где P (x) и Q (x) — многочлены (Q (x) = 0), сводится к решению уравнения P (x) = 0 и проверке того, что корни удовлетворяют условию Q (x)= 0.

Дробно-рациональные уравнения. Так называется уравнение, которое содержит кроме многочленов еще и дробно-рациональные функции.

Алгоритм решения:

1. Найти область допустимых значений уравнения.

2. Решить целое рациональное уравнения.

3. Найти те значения параметра, при которых найденные корни целого рационального уравнения являются посторонними.

4. Сформулировать ответ.

Пример 1. Решить относительно х:

3mx-5\(m-1)(x+3)+(3m-11)\m-1=(2x+7)\(x+3)|

ОДЗ: (m-1)(x+3)= 0, то есть m = 1, x = –3.

Умножив обе части уравнения на (m-1)(x+3), получим уравнение ,

mx-5(3m-1)(x+3)=(2x+7)(m-1) получаем,

x(4m-9)=31-2m

Отсюда при m = 2,25 . x= (31-2m)\(4m-9)

Теперь необходимо проверить, нет ли таких значений m, при которых найденное значение x равно –3.

x(4m-9)=31-2m , решая это уравнение, получаем, что х равен –3 при т = –0,4.

Ответ: при т = 1, т = 2,25, т = –0,4 уравнение (1) имеет единственное решение ; при т = 2,25 и при т = –0,4 решений нет, при т = 1 уравнение (1) не имеет смысла.

Пример 2. Решить уравнение x\x+1= а.

Решение. Очевидно, х ≠-1. Приведем исходное уравнение к виду: (1 – а)х = а, заметим, что при а = 1 уравнение не имеет корней, а при а ≠ 1 получаем х = a\a-1 .

Проверим нет ли таких значений а, при которых найденное значение х равно – 1, т. е. нужно решить уравнение - 1 = a\a-1 относительно а.

Так как последнее уравнение не имеет корней, других вариантов, кроме рассмотренных выше, не имеется

Ответ: 1) если а ≠1 1, то х=(а-1)\а ; 2) если а=1 , то корней нет.

Преобразуем и получим уравнение 2ах = 1 – а, которое при а = 0 не имеет корней, а при а = 0.

Теперь проверим, нет ли таких значений параметра а, при которых найденное значение х было бы равно – 3 или 2.

Для этого решим относительно, а уравнения:

-3=(1-a)\2a и 2=(1-a)\2a

Корень первого уравнения - 0,2, корень второго уравнения 0,2; т. е. при а = ± 0,2 соответствующие значения х не входят в область определения исходного уравнения.

Ответ: 1) если а=-1 и а=0 , a=+2то корней нет;

2) если а≠1 ;а≠0 ; a≠-2, то x=(1-a)\2a .

Пример 4: Решите уравнение y\y²-xy -1\x-y=1

а) относительно x;

б) относительно y.

Решение.

а) Найдем недопустимые значения y: y=0, x = y, y²=y²–2y,

y=0 – недопустимое значение параметра y.

Если y≠0, то x=y–2; если y=0, то уравнение теряет смысл.

б) Найдем недопустимые значения параметра x: y=x, 2x–x²+x²=0, x=0 – недопустимое значение параметра x; y(2+x–y)=0, y=0 или y=2+x;

y=0 не удовлетворяет условию y(y–x) №0.

Ответ: а) если y=0, то уравнение теряет смысл; если y№0, то x=y–2;

б) если x=0, то уравнение теряет смысл; если x№0, то y=2+x.

D = (3a + 2)² – 4a (a + 1)²= 9a² + 12a + 4 – 8a² – 8a,

D = (a + 2)2.

Если a≠0 или a≠ – 1, то x=(3a+2-a-2) \2a(a+1) =2\a или x= (3a+2-a-2 )\2a(a+1)=1\(a+1) 4
Ответ: 5.

Подводя итог изученного в первой главе, можно отметить, что в процессе решения его при помощи приведения к общему знаменателю оно заменяется целым алгебраическим уравнением. Целое уравнение по отношению к данному является следствием и может иметь посторонние корни.

Отбор посторонних корней и выяснение условий, при которых корни уравнения-следствия являются корнями данного уравнения, представляют собой существенную часть решения дробно-рационального уравнения.
Глава 2. Методики решения рациональных уравнений с модулями

2.1. Основные способы, используемые при решении уравнений, содержащих модуль.

Корнями уравнения называются значения переменной, при которых уравнение обращается в верное равенство.

Решить уравнение – значит, найти все его корни или доказать, что корней нет.

Уравнением с модулем называют равенство, содержащее переменную под знаком модуля.

При решении уравнений, содержащих знак абсолютной величины, мы будем основываться на определении модуля числа и свойствах абсолютной величины числа. [8]

Свойства отражены на рисунке 1.

Рисунок 1. Свойства модуля

Существует несколько способов решения уравнений с модулем. Рассмотрим каждый из них.

-Метод последовательного раскрытия модуля.

Пример 1. Решим уравнение |х-5|=4.

Исходя из определения модуля, произведем следующие рассуждения. Если выражение, стоящее под знаком модуля неотрицательно, то есть х-5≥0, то уравнение примет вид х-5=4. Если значение выражения под знаком модуля отрицательно, то по определению оно будет равно – (х-5) =4 или х-5= -4.

Решая полученные уравнения, находим: х1=9, х2=1.
Ответ: 9;1.

Решим этим же способом уравнение, содержащее «модуль в модуле».

Пример 2. Решим уравнение ||2х-1|-4|=6

Рассуждая аналогично, рассмотрим два случая.
1). |2х-1|-4=6, |2х-1|=10. Используя еще раз определение модуля, получим: 2х-1=10 либо 2х-1= -10.

Откуда х1=5,5, х2= -4,5.2). |2х-1|-4= -6, |2х-1|= -2.

Понятно, что в этом случае уравнение не имеет решений, так как по определению модуль всегда неотрицателен.
Ответ: 5,5; -4,5.

Метод интервалов – это метод разбиения числовой прямой на промежутки, в которых по определению модуля знак абсолютной величины можно будет снять.

Рисунок 2 Метод интервалов

Для каждого из промежутков необходимо решить уравнение и сделать вывод относительно получившихся корней. Корни, удовлетворяющие промежуткам, и дадут окончательный ответ. Данный пример отражен на рисунке 2.

Пример 3. Решим уравнение |х+3|+|х-1|=6.
Найдем корни (нули) каждого выражения, содержащегося под знаком модуля: х+3=0, х= -3; х-1=0, х=1. Эти значения х разбивают числовую прямую на три промежутка:-3

Решим уравнение отдельно в каждом из получившихся промежутков. В первом промежутке (х < -3) оба выражения, стоящие под знаком модуля отрицательны, поэтому при записи уравнения без абсолютной величины знаки этих выражений меняем на противоположные.

Получим уравнение: -х-3-х+1=6. Откуда х= -4. Число -4 является решением данного уравнения, так как оно принадлежит рассматриваемому промежутку.

Во втором промежутке (-3 ≤ х < 1) первое выражение положительно, а второе отрицательно. Рассуждая аналогично, получим уравнение: х+1-х+1=6, откуда получаем неверное числовое равенство, то есть в рассматриваемом промежутке уравнение корней не имеет. В последнем промежутке (х ≥ 1) оба выражения положительны, поэтому уравнение записывается так: х+3+х-1=6. Откуда х=2. Это значение удовлетворяет неравенству х ≥ 1. Ответ: -4; 2.

Пример 4. |2-х|=2х+1.

Прежде всего, следует установить область допустимых значений. Возникает естественный вопрос, почему в предыдущих примерах не было необходимости этого делать. В этом уравнении в правой части стоит выражение с переменной, которое может быть отрицательным. Таким образом, область допустимых значений – это промежуток [-½; +∞). Найдем нуль выражения, стоящего под знаком модуля: 2-х=0, х=2.
В первом промежутке: 2-х=2х+1, х=⅓. [9]

Это значение принадлежит ОДЗ, значит, является корнем уравнения.
Во втором промежутке: -2+х=2х+1, х= -3. -3 не принадлежит ОДЗ, а следовательно не является корнем уравнения. Ответ: ⅓.

-Метод графиков. Суть данного метода заключается в использовании графиков функций для нахождения корней уравнения. Этот метод реже других применяют для решения уравнений, содержащих модуль, так как, во-первых, он занимает достаточно много времени и не всегда рационален, а, во-вторых, результаты, полученные при построении графиков, не всегда являются точными.

Преобразуем уравнение: 1 + |x| = 0.5

|x| =0.5-1

|x|=-0.5

Графиком функции являются лучи - биссектрисы 1-го и 2-го координатных углов. Графиком функции является прямая, параллельная оси OX и проходящая через точку -0,5 на оси OY.(Рисунок 3)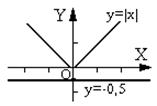

Рисунок 3. График функции

Графики не пересекаются, значит, уравнение не имеет решений.

Ответ: нет решений.

Пример 5. |х+1|=2. Построим графики функций у=|х+1| и у=2.
Для построения графика у=|х+1|, построим график функции у=х+1, а затем отразим часть прямой, лежащую ниже оси ОХ.

Абсциссы точек пересечения графиков и есть корни уравнения: х₁=1, х₂= -3. Ответ: 1; -3.

Пример 6. |х²-1|=|4-х²|.Построим графики функций у=|х²-1| и у=|4-х²|. Для этого построим графики функций у= х²-1 и у=4-х², а затем отобразим часть графиков, лежащую ниже оси ОХ. х₁≈1,6; х₂≈-1,6.

-Метод решения при помощи зависимостей между числами а и в, их модулями и квадратами этих чисел. Опорная информация:|а|=|в|

а=в или а=-в; а²=в² а=в или а=-в; (1)
|а|=|в|

а²=в² (2)

Пример 7. Решим уравнение |х²-8х+5|=|х²-5|.
Учитывая соотношение (1), получим:
х²-8х+5= х²-5 или х²-8х+5= -х²+5 х=1,25 х=0 или х=4.

Таким образом, корни исходного уравнения: х₁=1,25; х₂=0; х₃=4.

Ответ: 1,25; 0; 4.

Пример 8. |х+3|=|х-5|.

В силу соотношения (2) получаем: (х+3)²=(х-5)²; х²+6х+9= х²-10х+25; х=1.

Ответ:1.

Пример 9. (1-3х)²=(х-2)². Учитывая соотношение (2), получаем: |1-3х|=|х-2|, откуда из соотношения (1), имеем: 1-3х=х-2 или 1-3х= -х+2 х=0,75 х= -0,5. Ответ: 0,75; -0,5

- Использование геометрической интерпретации модуля. Опорная информация: геометрический смысл модуля разности величин – это расстояние между ними. Например, геометрический смысл выражения |х-а| - длина отрезка координатной оси, соединяющей точки с абсциссами а и х. Перевод алгебраической задачи на геометрический язык часто позволяет избежать громоздких решений.

Пример 10. |х-2|+|х-3|=1. Исходя из геометрической интерпретации модуля, левая часть уравнения представляет собой сумму расстояний от некоторой точки с абсциссой х до двух фиксированных точек с абсциссами 2 и 3. Тогда очевидно, что все точки с абсциссами, принадлежащими отрезку [2;3] обладают требуемым свойством, а точки, расположенные вне этого отрезка – нет. [9]

Отсюда, множеством решений уравнения является отрезок [2;3].

Ответ: [2;3]

Пример 11. |х-2|-|х-3|=1.

Рассуждая аналогично, получим, что разность расстояний до точек с абсциссами 2 и 3 равна 1 только для точек, расположенных на координатной оси правее числа 3. Следовательно, решением данного уравнения будет являться луч, выходящий из точки 3, и направленный в положительном направлении оси ОХ.

Ответ: [3;+∞).

Обобщением вышеприведенных уравнений 10 и 11 являются следующие равносильные переходы: |х-а|+|х-в|=в-а, где в ≥ а а ≤ х ≤ в

|х-а|-|х-в|=в-а, где в ≥ а х ≥ в

Проанализировав представленные способы решения уравнений, содержащих модуль, можно сделать вывод, что ни один из них не является универсальным и для получения наилучших результатов необходимо добиваться того, чтобы ученик овладел возможно большим количеством методов решения, оставляя право выбора решения за собой.

Решим аналитически и графически уравнение |x - 2| = 3.

Решение.

А) Аналитическое решение

1-й способ

Рассуждать будем, исходя из определения модуля. Если выражение, находящееся под модулем неотрицательно, т. е. x - 2

0, тогда оно "выйдет" из под знака модуля со знаком "плюс" и уравнение примет вид: x - 2 = 3. Если значения выражения под знаком модуля отрицательно, тогда, по определению, оно будет равно:

x - 2=-3

Теперь можно сделать вывод: если модуль некоторого выражения равен действительному положительному числу a, тогда выражение под модулем равно либо a.

Б)Графическое решение

Одним из способов решения уравнений, содержащих модуль, является графический способ.

Суть этого способа заключается в том, чтобы построить графики данных функций. В случае, если графики пересекутся, точки пересечений данных графиков будут являться корнями нашего уравнения.

В случае, если графики не пересекутся, мы сможем сделать вывод, что уравнение корней не имеет. Этот способ, вероятно, реже других применяют для решения уравнений, содержащих модуль, так как, во-первых, он занимает достаточно много времени и не всегда рационален, а, во-вторых, результаты, полученные при построении графиков, не всегда являются точными. [7]

Другой способ решения уравнений, содержащих модуль - это способ разбиения числовой прямой на промежутки. В этом случае нам нужно разбить числовую прямую так, что по определению модуля, знак абсолютной величины на данных промежутках можно будет снять.

Установим, при каких значениях x, модуль равен нулю: х-2=0,х=2.

Получим два промежутка, на каждом из которых решим уравнение (рисунок 4):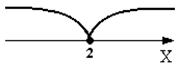

Рисунок 4. Графический способ решения

Ответ. Если y=0, то уравнение не имеет смысла; если y=–1, то x – любое целое число, кроме нуля; если y≠0, y≠– 1, то решений нет.

Графиком функции у= 3 является прямая, параллельная оси OX и проходящая через точку (0; 3) на оси OY.(Рисунок 5)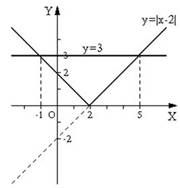

Рисунок 5 . График функций

Затем, для каждого из промежутков мы должны будем решить данное уравнение и сделать вывод, относительно получившихся корней (удовлетворяют они нашему промежутку или нет). Корни, удовлетворяющие промежутки и дадут окончательный ответ. Каждый интервал включает в себя левый конец и не включает правый.

На первый взгляд, такая запись может показаться неудобной, нелогичной и вообще какой-то бредовой. Но поверьте: после небольшой тренировки вы обнаружите, что именно такой подход наиболее надёжен и при этом не мешает однозначно раскрывать модули.

Лучше уж использовать такую схему, чем каждый раз думать: отдавать левый/правый конец в текущий интервал или «перекидывать» его в следующий.

Однако неумение правильно рассказать эту тему и общий недостаток времени в школьной сетке занятий приводят к тому, что большинство учеников путаются в этой теме и допускают обидные ошибки.

Поэтому сегодня на примере простых уравнений мы разберем сразу два ключевых приема, с помощью которых решатся все уравнения, содержащие один знак модуля.

Важно понимать, что второй прием является следствием первого, поэтому применять его «слепо», без понимания того, как работает оригинальная формула — это почти гарантированный путь к ошибкам и плохим оценкам.

2.2. Методы повышения эффективности изучения рациональных уравнений с модулем

Кодификатор требований к уровню подготовки обучающихся для проведения основного государственного экзамена по математике является одним из документов, определяющих структуру и содержание КИМов. В нем сформулированы требования к уровню подготовки выпускников основной школы. [2] Для повышения эффективности изучения данных уравнений необходимо выделить компетенции, представленные в таблице 1.

Таблица 1. Необходимые компетенции

Код раздела	Код контролируемого умения	Уметь решать уравнения, неравенства и их системы
3	3.1	Решать линейные, квадратные уравнения и рациональные уравнения, сводящиеся к ним, системы двух линейных уравнений и несложные нелинейные системы
	3.2	Решать линейные и квадратные неравенства с одной переменной и их системы
	3.3	Применять графические представления при решении уравнений, систем, неравенств
	3.4	Решать текстовые задачи алгебраическим методом, интерпретировать полученный результат, проводить отбор решений исходя из формулировки задачи

Тема «Дробные рациональные уравнения» впервые знакомится с учащимися на уроках алгебры в 8-м классе. Вводится понятие дробно-рационального уравнения, указывается четкий алгоритм его решения, анализируются основные примеры.

В 9 классе при изучении главы II «Уравнения и неравенства с одной переменной» мы расширяем знания учащихся по теме «Дробные рациональные уравнения», решаем более сложные задачи. Результаты обучения во многом зависят от конкретной методики преподавания, которую использует учитель на уроке.

Преподаватель в активном сотрудничестве с учащимися должен помочь им определить систему общих указаний, которые послужат ориентиром при решении уравнений.

Желательно четко сформулировать алгоритм решения дробно-рационального уравнения:

1) найти общий знаменатель дробей, входящих в уравнение;

2) умножить обе части уравнения на общий знаменатель;

3) решить полученное уравнение целиком;

4) исключить из своих корней те, которые обращают общий знаменатель в нуль.

В ходе решения дробно-рациональных уравнений необходимо установить, являются ли найденные корни всего уравнения допустимыми значениями переменной. Студенты часто допускают ошибки, пропуская этот момент, поэтому нужно настойчиво следить за тем, чтобы в каждом конкретном случае алгоритм был выполнен до конца.

Важно научить учащихся пользоваться «методом пристального взгляда», чтобы они наглядно видели разложение знаменателей на простые множители и точно находили наименьший общий знаменатель. Этот метод решения уравнений позволяет учащимся избегать ошибок при решении дробно-рациональных уравнений, успешно решать задачи с использованием дробно-рациональных уравнений.

Также необходимо предварительно отработать умения и навыки учащихся при выполнении тождественных преобразований, решении квадратных и линейных уравнений, разложении квадратного трехчлена на множители, нахождении ОДЗ, основного свойства пропорции, формул сокращенного умножения

Методы решения дробно-рациональных уравнений находят естественное и важное применение при решении текстовых задач. При решении текстовой задачи учащиеся выполняют три этапа, входящие в процесс решения:

- перевести задачу на язык алгебры (составить математическую модель),

- решить полученное уравнение,

- провести содержательный анализ полученного ответа.

В практической деятельности при проведении занятий по данной теме используют организацию учебной деятельности следующим образом: учащиеся работают в группах.

Одна группа решает текстовые задачи – им необходимо в процессе решения получить дробно-рациональное уравнение. Другая группа работает над решением тех же уравнений.

Контрольная проверка у доски работы двух групп представляет полное решение текстовой задачи с обоснованной записью ответа.

Все выпускники 9 класса должны уметь решать дробно-рациональные уравнения.

Подводя итог, можно отметить, что для достижения поставленной задачи учитель должен руководствоваться методическими требованиями к системе упражнений, направленных на организацию усвоения способов решения дробно-рациональных уравнений.

1. Система упражнений должна обеспечивать возможность активного участия учащихся в разработке метода решения рассматриваемого класса задач (в нашем случае решения дробно-рациональных уравнений)

2. система упражнений должна обеспечивать усвоение и необходимое повторение каждого из приемов, входящих как неотъемлемая часть формируемого приема (решения дробно-рациональных уравнений)

3. Система упражнений должна строиться по принципу планомерного, постепенного усложнения, содержать задачи комплексного характера, выполнение которых требует опознания типа уравнения и осознанного выбора способа его решения.

Заключение

Для формирования умения решать дробно-рациональные уравнения у всех учащихся 9 класса учителю математики необходимо разработать систему упражнений, направленных на отработку приемов и способов решения этих уравнений.

На этапе подготовки - создать условия для активного восприятия, через упражнения на повторение, упражнения пропедевтического характера.

На этапе усвоения - через систему упражнений необходимо создать условия, позволяющие учащимся осознать и прочно запомнить новую информацию (последовательность действий, алгоритм).

На этапе закрепления - создать условия для усвоения знаний в процессе их применения в различных ситуациях.

В зависимости от размера класса, таким образом может быть организована работа четырех или шести групп. Такая организация урока позволяет активизировать мыслительную деятельность учащихся, развивает коммуникативные навыки, умение работать в сотрудничестве позволяет закрепить умение решать текстовые задачи и одновременно умение решать дробно-рациональное уравнение.

Список литературы

1. Алимова Ш.А., Макарычев Ю.Н. и др. Учебник по алгебре 8 класса - 18 изд. - М.: Просвещение,2018. – 232 с.

2. Алимова Ш.А., Макарычев Ю.Н. и др. Учебник по алгебре 9 класса – 18 изд. – М.: Просвещение,2017. – 251 с.

3. Гусев В.А., Мордкович А.Г. Математика. Справочные материалы – 6 изд. – М.: Просвещение, 2018. – 183 с.

4. Локоть В.В., Задачи с параметром. Учебное пособие. – 2 изд., испр. и доп. – М.:АРКТИ, 2015. - 96 с.

5. Лупенко Г.В., Рурукин А.Н., Масленникова И.А., Поурочные разработки по алгебре: 7 класс к учебникам Макарычева Ю.Н., Алимова Ш.А. – М.: ВАКО, 2019. – 419 с.

6. Лупенко Г.В., Рурукин А.Н., Масленникова И.А. Поурочные разработки по алгебре: 8 класс к учебникам Алимова Ш.А., Макарычев Ю.Н. – М.: ВАКО, 2020. – 400 с.

7. Лупенко Г.В., Рурукин А.Н. и др. Поурочные разработки по алгебре: 9 класс к учебникам Алимова Ш.А., Макарычева Ю.Н. – М.: ВАКО, 2020. – 416 с.

8. Макарычев Ю.Н., Миндюк Н.Г., Нешков К.И., Суворова С.В. под редакцией Теляковского С.А. Учебник по алгебре 7 класса – 18 изд. – М.: Просвещение, 2019. – 240 с.

9. Мерзляк А.Г., Алгебраический тренажер: пособие для школьников и абитуриентов. А.Г. Мерзляк, В.Б. Полонский, М.С. Якир - М.: "Илексо" Харьков: "Гимназия" 2018, 156 с.

10. Симонов Д.С., Система тренировочных задач и упражнений по математике, Д.С. Бакаев, А.Г. Эпельман, А.А. Бесчинская, Р.М. Мостовой, А.Л. Абрамов - М.: Просвещение, 2017, 214 с.