Инвестиции. Курсовая работа тема Жизненный цикл инвестиционного проекта
 Скачать 498 Kb. Скачать 498 Kb.
|
|
Задача 12. Необходимо определить текущую стоимость аннуитета, равного 500 тыс. руб. при ставке дисконтирования 12% и сроке – 15 лет. Решение: Текущую стоимость аннуитета рассчитаем по формуле: A – сумма аннуитетного платежа, r – ставка дисконтирования, n – количество лет, PV – текущая стоимость аннуитета, Таким образом, Также текущую стоимость аннуитета можно определить используя специальные таблицы сложных процентов. Определим фактор текущей стоимости аннуитета по таблице сложных процентов в колонке, соответствующей ставке дисконтирования 12% и строке, соответствующей периоду существования аннуитета 15 лет. Он равен 6,81086. Текущая стоимость аннуитета равна произведению аннуитетного платежа на фактор текущей стоимости аннуитета, то есть 500 тыс.руб. * 6,81086 = 3 405,43 тыс.руб. Ответ: Текущая стоимость аннуитета равна 3 405,43 тыс.руб. Задача 13. Необходимо дать заключение по инвестиционным проектам, исходя из показателей: чистого дисконтированного дохода, индекса рентабельности, внутренней нормы доходности и дисконтированного срока окупаемости. При этом ставка дисконтирования в регионе А равна 9%, а в регионе Б – 10%. Денежный поток по проекту (тыс. руб.):
Решение: Рассчитаем показатели инвестиционных проектов по регионам А и Б и представим их в сводной таблице:
Чистый дисконтированный доход рассчитаем по формуле: CFt – приток денежных средств в период t; r – барьерная ставка (ставка дисконтирования); n – сумммарное число периодов t = 1, 2, ..., n   Индекс рентабельности равен  Все отрицательные значения денежного потока будем считать инвестициями.  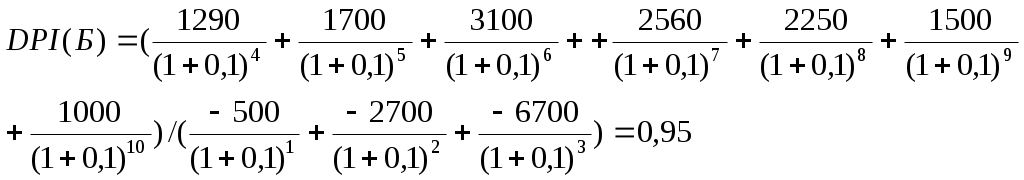 Индекс доходности в обоих случаях равен 0,95 или -5%, то есть отрицательное значение рентабельности, проект не приносит дохода. Внутренняя норма доходности определяет максимально приемлемую ставку дисконта, при которой можно инвестировать средства без каких-либо потерь для собственника. IRR = r, при котором NPV = f(r) = 0, Ее значение находят из следующего уравнения: Методом последовательных приближений рассчитаем значение IRR. IRR = 7,62% Исходя из показателей: чистого дисконтированного дохода, индекса рентабельности, внутренней нормы доходности и дисконтированного срока окупаемости проекты нерентабельны и не привлекательны для инвестирования как в регионе А, так и в регионе Б. Задача 14. В инвестиционную компанию поступили для рассмотрения бизнес-планы двух альтернативных проектов. Данные, характеризующие эти проекты, приведены ниже:
Ставка дисконтирования по проекту А принята в размере 10%, а проекта Б – 12% (в связи с более продолжительным сроком его реализации). Оценить проекты с точки зрения дисконтированного срока окупаемости и критерия NPV и выбрать наиболее эффективный из них. Решение: Срок окупаемости определяется как ожидаемое число лет, необходимое для полного возмещения инвестиционных затрат. Срок окупаемости рассчитаем по формуле: Ток – срок окупаемости инвестиций; n – число периодов; CFt – приток денежных средств в период t; Io – величина исходных инвестиций в нулевой период. Рассчитаем срок окупаемости проекта А. 1-й год 2-й год Рассчитаем срок окупаемости проекта В. 1-й год 2-й год 3-й год CFt – приток денежных средств в период t; r – барьерная ставка (ставка дисконтирования); It – сумма инвестиций (затраты) в t-ом периоде; n – сумммарное число периодов t = 1, 2, ..., n Рассчитаем NPV проекта А. Рассчитаем NPV проекта Б. Дисконтированный срок окупаемости проекта А – 2 года, а проекта Б – 3 года. В то же время NPV проекта А – 3 074 млн.руб., а NPV проекта Б – 4 528 млн.руб.. Таким образом, несмотря на более длительный срок окупаемости проект Б более интересный для инвестирования. Задача 15. Необходимо оценить эффективность инвестиционного проекта, используя простые и сложные методы оценки. Проект характеризуется следующими данными (млрд.руб.):
Решение: Простым сроком рассчитаем по формуле: где РР – срок окупаемости инвестиций (лет); Ко – первоначальные инвестиции; CFcг – среднегодовая стоимость денежных поступлений от реализации инвестиционного проекта. CFcг = (0 + 0 + 1 200 + 2 900 + 3 400 + 4 800 + 4 800) / 7 = 2 442,9 млрд.руб. РР = (1 950 + 3 900 + 2 000 + 1 200) / 2 442,9 = 3,7 лет. То есть на четвертом году от начала проекта он окупается. Расчетная норма прибыли отражает эффективность инвестиций в виде процентного отношения денежных поступлений к сумме первоначальных инвестиций: где ARR – расчетная норма прибыли инвестиций, ARR = 1/3,7 = 0,2699 или 26,99% Чистыми денежными поступлениями (Net Value, NV) называется накопленный эффект (сальдо денежного потока) за расчетный период: где Пm – приток денежных средств на m-м шаге; Оm – отток денежных средств на m-м шаге.
Задача 16. Предприятие планирует новые капитальные вложения в течение трех лет: 80 000 млн.руб. в первом году, 60 000 млн.руб. – во втором и 50 000 млн.руб. – в третьем. Инвестиционный проект рассчитан на 10 лет с полным освоением вновь введенных мощностей лишь на пятом году, когда планируемый годовой чистый денежный доход составит 75 000. Нарастание чистого годового денежного дохода в первые четыре года по плану составит 30, 40, 65, 95% соответственно от планируемого дохода 5-го года. Предприятие требует как минимум 18% отдачи при инвестировании денежных средств. Необходимо определить чистое современное значение инвестиционного проекта и дисконтированный срок окупаемости. Решение: Рассчитаем сумму чистых денежных доходов во всех периодах и составим таблицу:
1-ый год: 75 000 * 0,3 = 22 500 млн.руб., 2-ой год: 75 000 * 0,4 = 30 000 млн.руб., 3-ий год: 75 000 * 0,65 = 48 750 млн.руб., 4-ый год: 75 000 * 0,95 = 71 250 млн.руб.,  Проект окупается на шестом году его реализации. Проект рентабелен и привлекателен для инвестирования, NPV > 0 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
