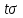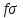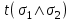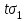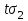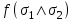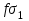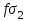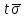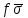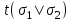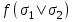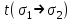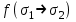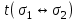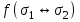Курсовая Елфимов МЛ. Курсовой проект по дисциплине Математическая логика и теория алгоритмов Тема Практические задачи математической логики и теории алгоритмов
 Скачать 369.02 Kb. Скачать 369.02 Kb.
|
3 Логический вывод в исчислении высказываний3.1 Метод прямого преобразованияВысказывание B есть логическое следствие высказываний 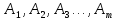 , то есть , то есть 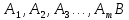 , если для всякого распределения истинностных значений, приписываемых каждой из простых формул , если для всякого распределения истинностных значений, приписываемых каждой из простых формул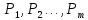 , входящих в одну или несколько из формул , входящих в одну или несколько из формул 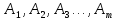 и в формулу B, формула B получает значение истина всякий раз, когда каждое значение и в формулу B, формула B получает значение истина всякий раз, когда каждое значение 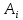 получает значение истина [6]. получает значение истина [6].Теорема 1. 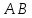 тогда и только тогда, когда импликация тогда и только тогда, когда импликация 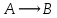 является тавтологией. является тавтологией. 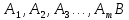 тогда и только тогда, когда тогда и только тогда, когда 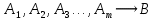 является тавтологией. является тавтологией.Теорема 2. Если импликация 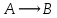 является тавтологией, то умозаключение будет правильным, то есть, является тавтологией, то умозаключение будет правильным, то есть, 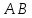 . .3.2 Метод семантических таблиц Методы доказательства – это алгоритмические процедуры, посредством которых можно установить, является ли данное высказывание тавтологией. Основой для построения семантических таблиц является атомарная семантическая таблица, [3] которая строится на основе законов исчисления высказываний Пусть 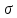 – высказывание. Обозначим через – высказывание. Обозначим через 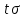 – утверждение « – утверждение «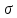 истинно», а через истинно», а через 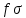 – утверждение « – утверждение «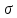 ложно». При этом – ложно». При этом – 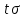 и и 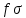 называются помеченными формулами. называются помеченными формулами.Таблица 4 – Атомарная семантическая таблица
Вершинами семантической таблицы называются все помеченные формулы, встречающиеся в таблице. Вершина семантической таблицы называется особой, если она встречается как корень некоторой атомарной семантической таблицы. В противном случае вершина называется обычной. Ветвь семантической таблицы называется противоречивой, если для некоторого высказывания помеченные формулы tσ и fσ являются вершинами этой ветви. Семантическая таблица называется замкнутой, если каждая непротиворечивая ее ветвь не содержит обычных вершин. В противном случае семантическая таблица называется незамкнутой. Семантическая таблица противоречива, если каждая ее ветвь противоречива. Доказательством или выводом по Бету высказывания 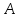 называется замкнутая противоречивая семантическая таблица, в корне которой помещена помеченная формула называется замкнутая противоречивая семантическая таблица, в корне которой помещена помеченная формула 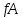 . Замкнутая противоречивая таблица, имеющая в качестве корня . Замкнутая противоречивая таблица, имеющая в качестве корня 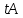 , называется опровержением по Бету высказывания , называется опровержением по Бету высказывания 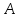 . .Итак, если замкнутая семантическая таблица с 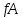 в корне противоречива (что означает, что мы всеми возможными способами пытались сделать высказывание в корне противоречива (что означает, что мы всеми возможными способами пытались сделать высказывание 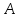 ложным и не сумели), то ложным и не сумели), то 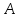 - тавтология. - тавтология.Если не все ветви семантической таблицы противоречивы, то это свидетельствует о том, при некоторой комбинации значений атомов, входящих в исходное выражение, это выражение будет истинным, а при другой комбинации - ложным, то есть, выражение не является тавтологией. |