Курсовая Елфимов МЛ. Курсовой проект по дисциплине Математическая логика и теория алгоритмов Тема Практические задачи математической логики и теории алгоритмов
 Скачать 369.02 Kb. Скачать 369.02 Kb.
|
5.2 Равносильности логики предикатовПомимо эквивалентностей логики высказываний для логики предикатов справедливы следующие эквивалентности[6] ( 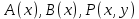 – предикаты, a – предикаты, a 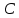 – высказывание): – высказывание):Комбинация кванторов: 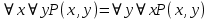 ; ;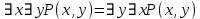 ; ;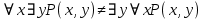 . .Комбинация кванторов и отрицаний: 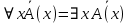 ; ;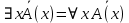 ; ;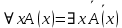 ; ;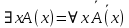 . .Расширение области действия кванторов ( 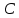 не зависит от не зависит от  ): ):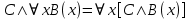 ; ; 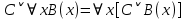 ; ;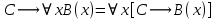 ; ;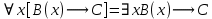 ; ;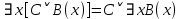 ; ;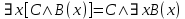 ; ;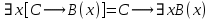 ; ;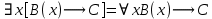 . .Расширение области действия кванторов: 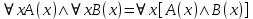 ; ;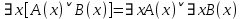 ; ;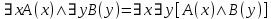 ; ; ; ;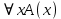 ˅ ˅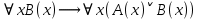 . .5.3 Предваренная и Сколемовская нормальные форма (ПНФ и СНФ)Нормальная форма. Формула логики предикатов имеет нормальную форму, если она содержит только операции конъюнкции, дизъюнкции и кванторные операции, а операция отрицания отнесена к элементарным формулам. Например, для формулы 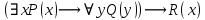 нормальной формой будет нормальной формой будет 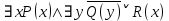 . .Предварённая нормальная форма (ПНФ) - нормальная форма, в которой кванторные операции либо полностью отсутствуют, либо они используются после всех операций алгебры логики. Например, для нормальной формы 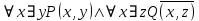 предваренной нормальной формой будет предваренной нормальной формой будет 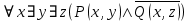 [5]. [5].Всякую формулу логики предикатов можно свести к ПНФ, если использовать следующий алгоритм: – исключение логических связок ⟷ и ⟶; – продвижение знака отрицания до атома. Многократно (пока это возможно) делаются замены; – переименование связанных переменных; – вынесение кванторов. Для вынесения кванторов используются формулы эквивалентности для исчисления предикатов. Переименовывать связанные переменные необходимо только в самом кванторе и в области действия этого квантора. Одинаковые переменные, для которых связывающие их кванторы имеют различные области действия, могут переименовываться разным образом или одна из них может переименовываться, а другая нет. Сколемовская нормальная форма (СНФ) строится в соответствии со следующими правилами: – формула логики предикатов представляется в ПНФ; – последовательно (слева направо) вычеркиваем каждый квантор существования, например 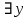 , заменяя все вхождения переменной y на новый еще не использованный функциональный символ f, в качестве аргументов f берем все переменные, связанные предшествующими , заменяя все вхождения переменной y на новый еще не использованный функциональный символ f, в качестве аргументов f берем все переменные, связанные предшествующими 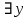 кванторами всеобщности. Функциональный символ f называется сколемовской функцией. кванторами всеобщности. Функциональный символ f называется сколемовской функцией.Формула логики предикатов, полученная после выполнения шагов 1 и 2, называется сколемовской нормальной формой (СНФ). Практическое задание №6 Привести формулу к предваренной нормальной форме (ПНФ) и сколемовской нормальной форме (СНФ): 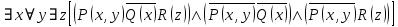 Сначала приведём формулу к виду ПНФ. 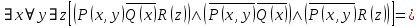 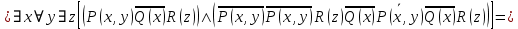 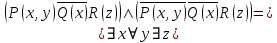 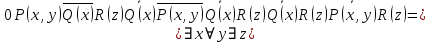 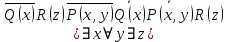 – ПНФ – ПНФТеперь из полученной ПНФ можем получить СНФ в соответствии с описанными ранее правилами. 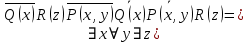 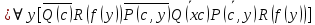 – СНФ – СНФ7 Программирование на языке ПрологТеория алгоритмов является частью математической логики, изучает общие свойства и закономерности алгоритмов, а также разнообразные формальные модели и их представление. Используется для исследования проблемы разрешимости и обоснования математики. Большинство задач логики можно решить с помощью Пролога. Язык пролог используется для решения логических задач. Первая версия была разработана в 1973 г. Логическое программирование - метод решения задач, основанный на логике. Язык программирования – Пролог. История создания языка связана с осознанием возможности построения универсальной модели преобразования символьных данных при решении задач искусственного интеллекта - языки и методы решения таких задач впервые реализованы в системах SmallTalk, Planner, Lisp. В программах на Прологе существует три типа предложений (clauses): факт, правило вывода, цель. Программа Пролога включает определенные разделы, не все из которых являются обязательными: – раздел domains – описание типов данных объектов; – раздел predicates – раздел для описания всех отношений, используемых в программе. Факты и правила, входящие в раздел clauses, представляют собой отношения (предикаты), которые связывают один или несколько объектов; – раздел goal – раздел для введения цели, задания. Ввод цели можно рассматривать как формулирование запроса к базе знаний, ответ на который строится самой Пролог-программой; – раздел clauses, содержит множество фактов и правил. В программе по крайней мере должны быть разделы predicates и clauses. Раздел domains напоминает объявление данных в традиционных языках, например, таких, как Паскаль и Си. Существуют следующие типы доменов: – char (символьный); – integer (целый); – real (вещественный); – string (строковый); – symbol (для цепочки из букв, цифр и символов подчеркивания с первой строчной буквой либо цепочки знаков в двойных кавычках); – file (файловый). По отношению к именам объектов (идентификаторам) в Прологе используются следующие правила: – имя может включать латинские буквы, цифры и символ подчеркивания, причем первым символом не должна быть цифра; – имена символических констант должны начинаться со строчной буквы; – в имени можно использовать одновременно и строчные и прописные буквы. Практическое задание №7 Известно, что: Кате нравится фигурное катание; Коле нравится футбол; Рите нравится бейсбол; Игорю нравится плавание; Лизе нравится футбол; Данилу нравится программирование; Ольге нравится плавание. Записать факты на Прологе и ответить на вопросы: Кому нравится программирование? Что нравится Рите? Кто занимается одинаковыми видами спорта? Листинг программы представлен ниже. domains C=symbol predicates nondeterm likes(C,C) nondeterm liked_the_same_thing(C) clauses likes(katya,figure_skating). likes(kolya,football). likes(rita,baseball). likes(igor,swimming). likes(lisa,football). likes(danil,programming). likes(olga,swimming). liked_the_same_thing(Z):-likes(Z,swimming). liked_the_same_thing(Z):-likes(Z,football). goal %likes(X,programming). %likes(rita,X). liked_the_same_thing(X). Примеры работы программы представлен ниже (рисунки 7, 8 и 9). 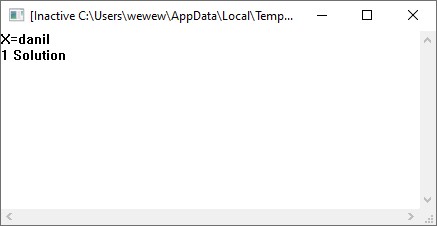 Рисунок 7 – Ответ на вопрос (Кому нравится программирование?) 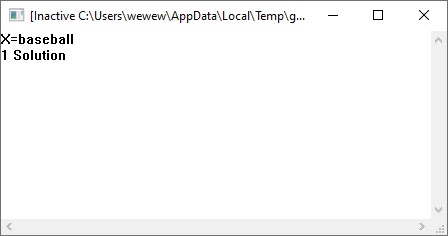 Рисунок 8 – Ответ на вопрос (Что нравится Рите?) 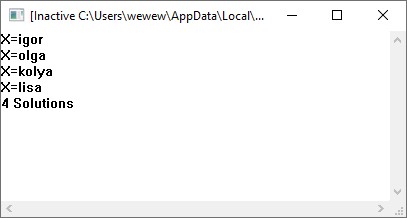 Рисунок 9 – Ответ на вопрос (Кто занимается одинаковыми видами спорта?) ЗАКЛЮЧЕНИЕ Работая над данным курсовым проектом, я осознал, усвоил и закрепил некоторые темы математической логики, я так же закрепил полученные мной ранее теоретические сведение, которые обязательно пригодятся мне в будущем, так как сфера применения математической логики довольно широка. Так же математическая логика прекрасно развивает, как бы то ни было странно, логическое мышление. Так же большим плюсом, по моему мнению, является то, что математическая логика позволяет переводить высказывания из естественного языка в язык алгебры логики, что может сыграть большую роль в определенных жизненных ситуациях. Работа над данным курсовым проектом помогла мне разобраться в, различного вида, формах логических функций, в области логики кванторов и предикатов, составлении релейно-контактных схем, и, наконец, программировании на языке Пролог. Список литературы 1 Пономарев В.Ф. Математическая логика: учебное пособие / В.Ф. Пономарев. — Калининград: КГТУ, 2005. — 201с. 2 Методические указания к выполнению лабораторных работ 1-3 по дисциплине “Математическая логика и теория алгоритмов” для студентов специальности 230101 очной и сокращенной очной, сокращенной очной, заочной и сокращенной заочной форм обучения / ГОУВПО «Воронежский государственный технический университет»; сост. Л.В. Холопкина, М.П. Носачева. Воронеж, 2009. 47 с. 3 Лобарев Д.С. Теория алгоритмов: учебно-методическое пособие/ Д.С.Лобарев , 2016. -72 с. 4 Игошин В.И. Математическая логика и теория алгоритмов: учеб. пособие для студ. высш. учеб. заведений / В. И. Игошин. - 2-е изд., стер. - М. : Издательский центр «Академия», 2008. — 448 с. 5 Шаповалова, Л.Н. Дискретная математика. Математическая логика: учебное пособие / Л.Н. Шаповалова, В.В. Серегина. – Зерноград: Азово-Черноморский инженерный институт ФГБОУ ВО Донской ГАУ, 2015. – 69 с. 6 Колмогоров А.Н. Математическая логика: учебное пособие / А. Н. Колмогоров. — Москва: Ком.Книга, 2006. — 240 с. 7 Зарипова Э.Р. Лекции по дискретной математике: Учеб. Пособие. Математическая логика. / Э.Р. Зарипова , М.Г. Кокотчикова , Л.А. Севастьянов – М.: Изд-во РУДН, 2011. – 79 с. 8 Беляков А.Ю. Практика логического программирования на языке Пролог: Учебное пособие / А.Ю. Беляков М-во с.-х. РФ, федеральное гос. бюджетное образов. учреждение высшего образов. «Пермская гос. с.-х. акад. им. акад. Д.Н. Прянишникова». – Пермь: ИПЦ «Прокростъ», 2017. – 129 с. 9 Колмогоров А.Н. Математическая логика / А. Н. Колмогоров, А. Г. Драгалин. - 3-е изд., стер. — М.: КомКнига, 2006. — 240 с. 10 Большакова Е.И. Программирование на языке Пролог: учебное пособие / Е.И Большакова. — Москва: ВМК МГУ, 2013. - 112 с. |
