Курсовая Елфимов МЛ. Курсовой проект по дисциплине Математическая логика и теория алгоритмов Тема Практические задачи математической логики и теории алгоритмов
 Скачать 369.02 Kb. Скачать 369.02 Kb.
|
3.3 Метод резолюцийПропозициональные символы с отрицанием либо без отрицания, входящую в элементарную сумму (дизъюнкт), называют литералами (литерами) логики высказываний. Литеры 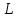 и и 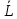 называют контрарными. называют контрарными.Резольвентой двух дизъюнктов 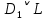 и и 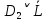 называется дизъюнкт называется дизъюнкт 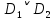 . .Теорема. Резольвента является логическим следствием порождающих ее дизъюнктов, то есть, 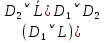 . .Метод резолюций [1] доказательства невыполнимости формулы 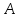 состоит в том, что эта формула представляется в КНФ и к ней конъюнктивно присоединяются все возможные резольвенты ее дизъюнктов и получаемых в процессе доказательства резольвент. Полнота метода резолюций состоит в том, что он гарантирует получение для формулы состоит в том, что эта формула представляется в КНФ и к ней конъюнктивно присоединяются все возможные резольвенты ее дизъюнктов и получаемых в процессе доказательства резольвент. Полнота метода резолюций состоит в том, что он гарантирует получение для формулы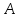 следствия false, если следствия false, если 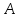 невыполнима. Если же, перебрав все возможные резольвенты формулы невыполнима. Если же, перебрав все возможные резольвенты формулы 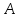 , мы не нашли пустую резольвенту, то , мы не нашли пустую резольвенту, то 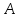 не является невыполнимой. не является невыполнимой.Так как доказательство проводится методом от противного, то вывод берется с отрицанием. Исходные посылки и вывод, взятый с отрицанием, представим в виде множества дизъюнктов и будем формировать возможные резольвенты с целью получения нулевой резольвенты. Получение нулевой резольвенты свидетельствует о невыполнимости исходной формулы, то есть, мы пытались всеми возможными методами подтвердить ложность вывода, но нам это не удалось. Следовательно, вывод является правильным. 3.4 Практическое задание №4Проверить правильность логического вывода методом прямого преобразования, методом семантических таблиц и методом резолюций: 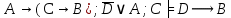 Докажем правильность логического вывода, используя метод прямых преобразований: 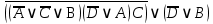 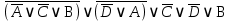 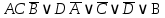 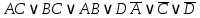 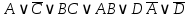 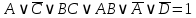 Чтобы проверить, что наши преобразования верны, построим таблицу истинности (рисунок 4) 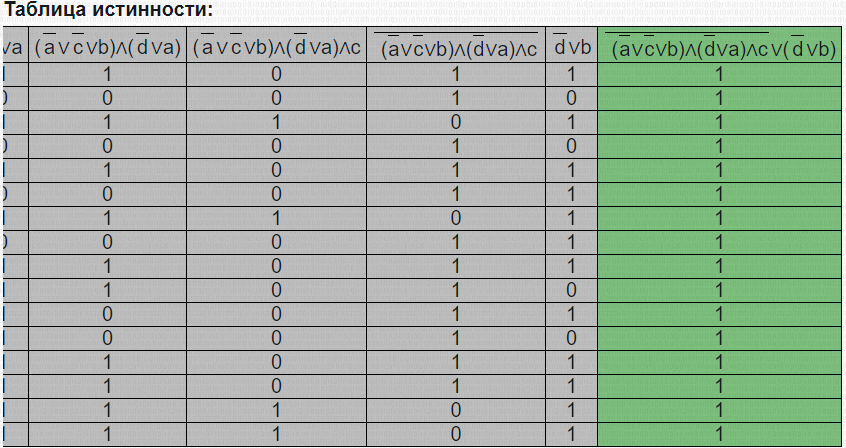 Рисунок 4 – таблица истинности исходной формулы Вывод оказался верным так как после прямого преобразования в таблице истинности получилась 1. Теперь решим воспользуемся методом семантических таблиц. Так как доказательство проводится от обратного, то пометим исходную формулу, как 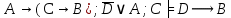 , тогда: , тогда: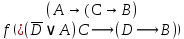 ↓ 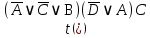 ↓ 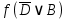 ↓ 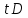 ↓ 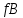 ↓ 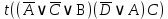 ↓ 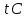 ↓ 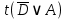 ↓ 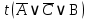 ↓ ↓ 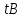 ↓ ↓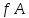 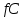 ↓ ↓ ↓ 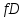 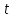 A AРисунок 5 – семантическая таблица Как видно каждая из ветвей семантической таблицы оказалась противоречивой, то есть, мы пытались всеми возможными методами подтвердить ложность вывода, но нам это не удалось. Следовательно, вывод является правильным. Рассмотрим применение метода резолюций. 1) 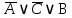 2) 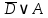 3) 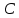 4) 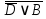 5) 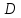 6) 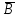 7) 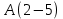 8) 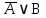 9) 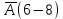 10) 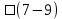 Путем перебора всех дизъюнктов, нам не удалось получить нулевую резольвенту. Мы пытались всеми возможными методами подтвердить ложность вывода, и нам это удалось. Следовательно, логический вывод является неправильным. |
