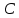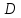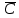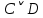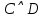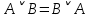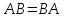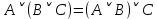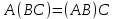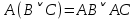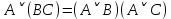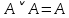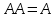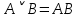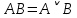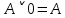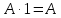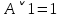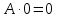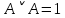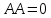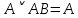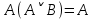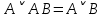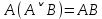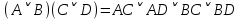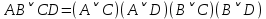Курсовая Елфимов МЛ. Курсовой проект по дисциплине Математическая логика и теория алгоритмов Тема Практические задачи математической логики и теории алгоритмов
 Скачать 369.02 Kb. Скачать 369.02 Kb.
|
1 Исчисление высказыванийВысказывание в математической логике — это повествовательное предложение, которое может быть классифицировано либо как истинное, либо как ложное, но ни как то или иное одновременно. Основными законами формальной логики являются: закон тождества: каждый из предметов, о которых идёт речь, всё время должен оставаться самим собой; закон противоречия: одно и то же высказывание нельзя одновременно утверждать и отрицать; закон исключения третьего: любое высказывание должно быть или истинным, или ложным. Третьего не дано. 1.1 Основные эквивалентности и функции исчисления высказываний Представим в виден таблицы 1 основные логические функции исчисления высказываний. Будем использовать высказывания C и D, принадлежащие множеству (0,1). Таблица 1 – Основные функции
В исчислении высказываний справедливы эквивалентности (равносильности) представленные в таблице 2. Таблица 2 – Основные эквивалентности
Практическое задание №1 Используя основные эквивалентности исчисления высказываний проверить следующие равносильности: 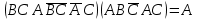 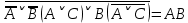 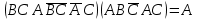 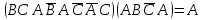 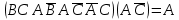 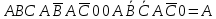 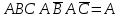 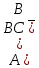 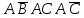 =A =A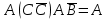 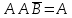 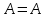 Левая и правая части оказались равны. Чтобы удостовериться в правильности решения, построим таблицу истинности исходной формулы (рисунок 1) с помощью программы Electronics Workbench. 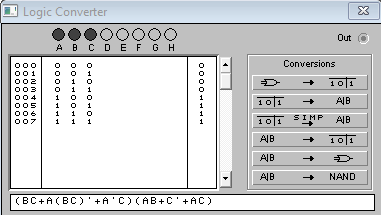 Рисунок 1 – Таблица истинности исходной формулы В результате построения видно, что исходная формула равна 1 только тогда, когда переменная A равна 1. Чтобы прировнять эти два высказывания нужно для начала упростить левую сторону. 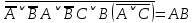 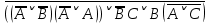 = = 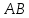 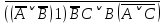 = = 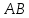 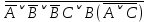 = = 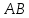 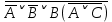 = = 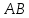 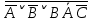 = = 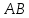 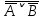 = = 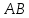 AB = 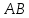 Левая и правая стороны оказались равны. Чтобы определиться правильно ли мы решили, построим таблицу истинности для исходной формулы (рисунок 2) и упрощённой (рисунок 3) с помощью программы Electronics Workbench. 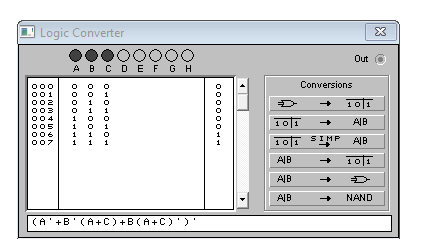 Рисунок 2 – Таблица истинности исходной формулы 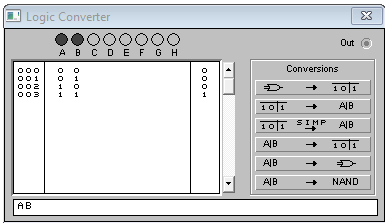 Рисунок 3 – Таблица истинности упрощённой формулы В результате мы видим, что таблицы истинности исходной и упрощённой формулы равны, следовательно, мы сделали всё правильно. |