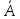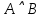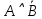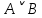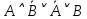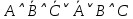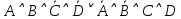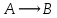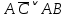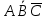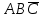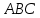Курсовая Елфимов МЛ. Курсовой проект по дисциплине Математическая логика и теория алгоритмов Тема Практические задачи математической логики и теории алгоритмов
 Скачать 369.02 Kb. Скачать 369.02 Kb.
|
1.2 Дизъюнктивная нормальная форма и конъюнктивная нормальная формаЭлементарной конъюнкцией называется конъюнкция, состоящая из переменных или их отрицаний. Дизъюнктивно-нормальная форма (ДНФ) [7] – дизъюнкция элементарных конъюнкций. Минимальной ДНФ называется та ДНФ, которая имеет самую короткую запись. В общем случае для получения минимальной ДНФ существуют эффективные алгоритмы, например, метод Квайна, карта Карно. Однако для получения минимальной ДНФ в некоторых частных случаях можно использовать следующие правила: если ДНФ является трехчленом, зависящим от трех переменных, и если симметрия нарушена только по одной из переменных, то устраняется тот член дизъюнкции, который эту переменную не содержит; если ДНФ является трехчленом, зависящим от трех переменных и если симметрия нарушена по двум из этих переменных, то данная ДНФ равносильна дизъюнкции, одним из членов которой является переменная, по которой симметрия не нарушена, а вторым членом служит тот член первоначальной ДНФ, который эту переменную не содержит. Также существует совершенная ДНФ (СДНФ), она должна удовлетворять следующим условиям: все элементарные конъюнкции различны; нет нулевых конъюнкций; ни одна из элементарных конъюнкций не содержит одинаковых членов; каждая элементарная конъюнкция содержит все переменные. Для получения СДНФ необходимо сначала найти минимальную ДНФ, а затем путем ввода дополнительных множителей добиться выполнения условия 4. Элементарной дизъюнкцией называется дизъюнкция, состоящая только из переменных или их отрицаний. Конъюнктивно-нормальной формой (КНФ) называется конъюнкция элементарных дизъюнкций. Минимальной КНФ называется такая КНФ, которая имеет самую короткую запись. Для получения минимальной КНФ, также, как и для получения ДНФ, в некоторых частных случаях можно использовать следующие правила: если КНФ зависит от трех переменных и представляет конъюнкцию трех элементарных дизъюнкций и если симметрия нарушена по одной из переменных, то поглощается та элементарная дизъюнкция, которая эту переменную не содержит; если КНФ зависит от трех переменных и представляет собой конъюнкцию трех элементарных дизъюнкций и если симметрия нарушена по двум из этих переменных, то данная КНФ равносильна конъюнкции, одним из членов которой является переменная, по которой симметрия не нарушена, а вторым членом является тот член первоначальной КНФ, который эту переменную не содержит. Практические задание №2 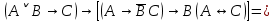 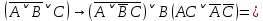 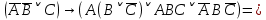 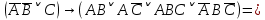 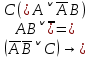 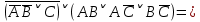 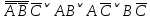 = =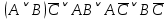 = =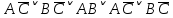 = = 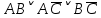 - ДНФ - ДНФ 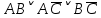 = = 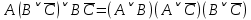 - КНФ - КНФ2 Перевод высказываний естественного языка на язык алгебры логики Язык алгебры логики может быть использован при решении большого числа содержательных логических задач. Решение таких задач с помощью логических рассуждений достаточно трудно. Если же применить аппарат алгебры логики к решению таких задач, то все рассуждения могут быть заменены на простые формализованные вычисления, гарантирующие правильность ответа. Но прежде чем применить формализованный подход, исходные рассуждения надо нужно правильно перевести на язык алгебры логики [2]. Для решения данной задачи может быть использована таблица соотношений между наиболее часто встречающимися выражениями естественного языка и формулами алгебры логики (таблица 3). Таблица 3 – Таблица соотношений
Продолжение таблицы 3
При переводе высказываний естественного языка на язык алгебры логики нужно выделить сначала элементарные высказывания и обозначить их символами так, чтобы по этим обозначениям можно было восстановить полный текст составного высказывания. Нужно стремиться к введению минимального количества элементарных высказываний, пытаясь выражать одни элементарные высказывания через другие. Практическое задание №3 Перевести высказывание естественного языка на язык исчисления высказываний Мать попросила сына купить цветы: либо гвоздики, либо розы; либо бордовые, либо красные; либо светлые, либо темные. Кроме того, должны быть выполнены следующие условия: - чтобы цветок был красным или гвоздикой, достаточно, чтобы он был темным. - цветок может быть бордовым, если он светлый - цветок может быть розой, если только он светлый и красный. Сначала выведем элементарные высказывания: А - Гвоздики 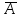 - Розы - РозыВ - Бордовые 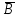 - Красные - КрасныеС - Светлые 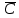 – Темные – ТемныеУсловия на языке алгебры логики будут представлены так: Чтобы цветок был красным или гвоздикой, достаточно, чтобы он был темным. 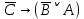 Цветок может быть бордовым, если он светлый. 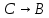 Цветок может быть розой, если только он светлый и красный. 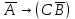 Для того чтобы узнать, что заказала мать, мы должны перемножить все получившиеся условия и после найти СДНФ: Перемножаем условия и сокращаем выражения: 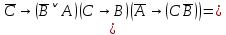 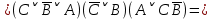 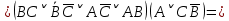 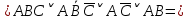  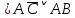 Теперь составим таблицу истинности и найдем СДНФ: Таблица 4 – Таблица истинности
СДНФ = 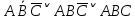 Получается, заказ матери состоял из: темных красных гвоздик, темных бордовых гвоздик и светлых бордовых гвоздик. Теперь узнаем, что купил сын, решив следующее выражение: 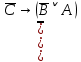 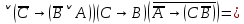 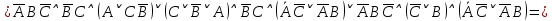 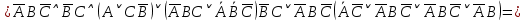 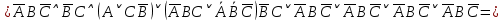 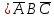 Получается, что сын купил: темные бордовые розы. |